Lang geleden kreeg ik een speciale 'puzzelkrant' onder ogen, gevuld met allerhande probleempjes zoals 'zoek de verschillen', woordladders, 'alfametics' (rekensommetjes waarin getallen door te achterhalen symbolen zijn vervangen), kruiswoordraadsels, et cetera. Mijn oog viel op een aardig uitziende puzzel, die wat moeilijker leek dan de rest van de opgaven. Het was een kruiswoordraadsel in getallen:

De letterlijke opdracht luidde: 'Maak de sommen kloppend met getallen gekozen uit $0, 1, 2, \dots, 25$.' Hierbij moet wel beseft worden dat er in elke 'rekenregel of -kolom' eigenlijk twee vergelijkingen staan, want er staan twee '$=$-tekens'. Zo moet de eerste regel gelezen worden als: $14 - a = b$ en $b - c = 7$.

Ik noem deze puzzelsoort een kruisgetalraadsel: een blok met getallen of cijfers, waarin een aantal 'kloppende sommen' staan, met bepaalde randvoorwaarden.

Opgave 1 Vind de unieke oplossing van dit kruisgetalraadsel.

In het 9-bij-9-kruisgetalraadsel van opgave 1 zijn 7 van de 25 getallen gegeven. Bovendien stonden de bewerkingen $+$, $-$, $\times$ en $:$ al vast. Onderstaande figuur is een 5-bij-5-kruisgetalraadsel waarbij helemaal niets vast staat, op de zes '$=$-tekens' na. Het vrije gebruik van bewerkingen zullen we ook bij de hierna volgende varianten aannemen. De $=$-tekens hebben steeds een vaste plek.

Het doel is in dit 'frame' positieve getallen te plaatsen, samen met zes bewerkingen, en daarmee zes juiste vergelijkingen te maken.

Een voorbeeld is:

Nu volgt een betrekkelijk voor de hand liggende vraag. 'Maak een kruisgetalraadsel met de cijfers $1$ tot en met $9$, waarbij elk cijfer maar één keer voor komt'. Helaas, in het boek Denkwaar (2010) staat een bewijs dat dit niet mogelijk is. Dus wordt de opdracht:

Opgave 2 Maak een kruisgetalraadsel met de getallen $1$ tot en met $10$, waarbij elk getal precies één keer  voorkomt, op één na.

 Er zijn er natuurlijk nog meer 'standaardwiskundige' bewerkingen. Naast de vier al gebruikte, zijn er machtsverheffen en de beide inverse bewerkingen hiervan, worteltrekken en de logaritme. De laatste twee hangen af van de keuze van de inverse bewerking voor grondtal of exponent, zodat er eigenlijk twee zestallen van bewerkingen zijn te onderscheiden:

$\color{blue}{(1)}$	$+\ -\ \times\ :\ x^y\ \sqrt[y]{x}$	($x$ variabel, $y$ vast)
$\color{blue}{(2)}$	$+\ -\ \times\ :\ x^y\ {}^x\!\log(y)$	($x$ vast, $y$ variabel)

In het kruisgetalraadsel komen precies zes vergelijkingen voor. Het ligt dus zeer voor de hand om voor elk van de twee zestallen te onderzoeken of er een kloppende invulling bestaat. Dat antwoord is ja, en levert leuke oefeningen in wiskundig rekenen op. We bekijken eerst systeem $\color{blue}{(1)}$. Om flauwe oplossingen te vermijden eisen we dat de wortel geen grondtal 1 mag hebben. Evenzo mag het grondtal bij een macht geen 1 zijn. We kunnen dit ook korter formuleren door te eisen dat de negen gebruikte getallen verschillend zijn. Het wordt dan een stuk moeilijker om een oplossing te vinden (de keuze van de zes bewerkingen over de zes vakken is vrij). Na lang zoeken vond ik een oplossing met onderling verschillende, gehele getallen, al zijn vier getallen negatief:

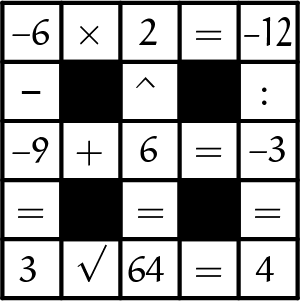
Uiteraard moet de laatste regel gelezen worden als $\sqrt[3]{64} = 4$. Een oplossing in systeem $\color{blue}{(2)}$, dus met '$\log$' in plaats van '$\sqrt{}$' is:

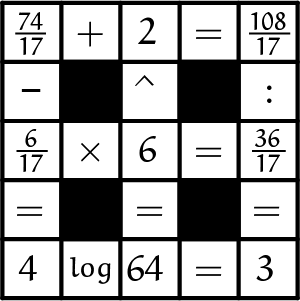
Opgave 3 Zoek een oplossing in systeem $\color{blue}{(1)}$ met negen onderling verschillende gehele getallen, waarvan er minder dan vier negatief zijn.

Opgave 4 Zoek een oplossing in systeem $\color{blue}{(2)}$ met negen onderling verschillende gehele getallen, waarvan er minder dan vier negatief zijn.

We bekijken ook een iets vrijere opdracht van een kruisgetalraadsel. Tot nu toe ging het over zes vergelijkingen ('sommen') in een 5-bij-5-frame, die steeds maximaal gekoppeld waren. Elke vergelijking is verbonden met precies drie andere. Maar we kunnen die strenge eis tot verbondenheid ook iets verzachten. In een gewoon kruiswoordframe zijn alle in te vullen woorden met minstens één ander woord verbonden. Dat kunnen we ook doen met de vergelijkingen. Als 'tegenprestatie' verlangen we dan wel alle cijfers $0$ tot en met $9$ aan te treffen. Dit zijn er natuurlijk 10, bestemd voor negen plaatsen, dus mogen we twee cijfers combineren. Alle in te vullen getallen/cijfers moeten wel positief zijn. Een oplossing met vijf vergelijkingen is dan bijvoorbeeld:

Opgave 5 Zoek nog een oplossing met vijf vergelijkingen, onderlinge verbondenheid en de cijfers $0$ tot en met $9$, waarvan er twee gekoppeld mogen worden.

Opgave 6 Er blijkt wel degelijk minstens één oplossing te bestaan voor het probleem uit opgave 5, maar dan met de oorspronkelijke zes vergelijkingen. Een aantal van die cijfers zijn dan echter wel negatief. Vind zo'n oplossing.

Zoals al eerder gezegd is het niet mogelijk is een 5-bij-5-blok met de cijfers $1$ tot en met $9$ te vullen met zes kloppende sommen. Maar is er dan geen variant te bedenken waarbij dat wel kan? Een van de mogelijkheden zou het '7-bij-5-blok' kunnen zijn. Hierin moeten dan de getallen $1$ tot en met $12$ worden ingevuld. De drie horizontale kennen nu een extra 'component'. Er wordt alleen gebruik gemaakt van de vier bewerkingen $+$, $-$, $\times$ en $:$. Een eerste voorbeeld is:

Een tweede oplossing is:

We houden ons uiteraard aan de rekenvolgorde, maar we gebruiken geen haakjes, dus de laatste horizontale vergelijking mag niet gelezen worden als $9 - (10 + 7)$. (Dat zou hier ook niet helpen, omdat het antwoord dan $-8$ zou zijn, en dat is niet toegestaan.) Ik vond ook nog een derde oplossing:

Deze drie oplossingen staan in het kort geleden gepubliceerde boek Denkwereld. De andere opgaven komen uit Denkwaar (2010), Denkwerk (2014) en Denkraam (2018).

Opgave 7 Vind nog een vierde oplossing. Minstens één van de zeven combinaties (vier verticale drietallen en drie horizontale viertallen) moet daarbij verschillen van die van de drie al gegeven oplossingen. Onder de inzenders van een vierde oplossing) worden drie door de auteur gesigneerde exemplaren van Denkwereld verloot. Stuur je antwoord uiterlijk 15 januari 2023 naar [email protected].