In dit artikel beschouwen we alleen echte ruimtelijke dimensies (Euclidische ruimte); het door sommigen geopperde
idee van de tijd als vierde dimensie komt hier niet aan de orde.

2- en 4-dimensionale werelden

Het is bekend dat van veel fysische verschijnselen de sterkte afneemt met de afstand, gelukkig maar. Die afname
gaat met $1/r^2$, en dat is het gevolg van onze $3$ dimensies. In een $2$-dimensionale wereld zouden ze afnemen met $1/r$, en in een $4$-dimensionale wereld met $1/r^3$. Dat geldt ook voor de zwaartekracht, maar dat heeft grote consequenties. Even aangenomen dat de traagheidswetten van Newton nog gewoon gelden, blijkt dat in een $4$-dimensionale ruimte geen stabiele planetenbanen kunnen zijn. In principe is het mogelijk dat een planeet een zuiver cirkelvormige baan om een ster beschrijft, maar als de snelheid ook maar iets toeneemt zal de planeet steeds verder van die ster verwijderd raken en uiteindelijk in de lege ruimte verdwijnen en daar bevriezen. En als de snelheid iets lager wordt komt de planeet steeds dichter bij de ster om daar uiteindelijk in te verdwijnen.

Figuur 1 Kat in een 2-dimensionale wereld? Omgekeerd, in een 2-dimensionale ruimte zijn de planetenbanen juist extra stabiel. Ontsnappen is niet mogelijk, hoe groot de snelheid van de planeet ook zal zijn, hij zal altijd weer bij de ster terugkeren. Dat impliceert dat het totale universum nooit heel erg groot kan zijn, maar dat mag de pret niet drukken. Maar er is nog wat anders. In een $2$-dimensionale wereld kunnen nooit complexe structuren ontstaan zoals onze hersenen. En de eventuele wezens in een $2D$ wereld kunnen niet een aparte in- en uitgang in hun lichaam hebben, anders splitsen ze zich in twee delen (zie figuur 1). Ze hebben dus maar één opening en daar komt alles door naar binnen en weer naar buiten, maar daar zijn ze aan gewend.

Dat neemt niet weg dat je wel kunt fantaseren over een $2$-dimensionale wereld. De auteur Edwin Abbott heeft daar een klassiek werk geschreven: FLATLAND, A Romance of Many Dimensions (1884), maar hij gaat vooral in op de sociale implicaties en niet op de fysica van die wereld.

Bovenstaande is niet bedoeld om aan te geven dat er geen $2$- of $4$-dimensionale werelden kunnen bestaan. Dat kan best, maar die werelden zullen er heel anders uitzien dan we gewend zijn in ons $3$-dimensionale leven. We kunnen wel nadenken over werelden met meer of minder dimensies, en in het volgende gaan we wat eenvoudige mathematische objecten bekijken: de kubus en de bol. In de wiskunde vormt het aantal dimensies geen enkele belemmering.

De kubus

Let op dat in het volgende de termen 'volume' en 'oppervlak' een ruimere betekenis hebben. Volume is de totale ruimte die door een object wordt ingenomen. Oppervlak is de som van de $(N - 1)$-dimensionale ruimtes die de $N$-dimensionale object begrenzen. Dus voor een simpel vierkant met ribbe $r$ is het 'volume' $r^2$ en het 'oppervlak' $4r$.

Een kubus is bekend bij iedereen, een rechthoekig blokje met gelijke lengte, breedte en hoogte. Maar wat is  bijvoorbeeld de $4$-dimensionale tegenhanger van de kubus? Om die te kunnen maken gaan we eerst na hoe een kubus is ontstaan uit meer eenvoudige objecten. Om een kubus te maken in één dimensie meer dan de huidige kubus is er een eenvoudig voorschrift:

Kopieer het object op zichzelf; verplaats dan één van de twee in de richting van de nieuwe dimensie waarbij overeenkomende hoekpunten door een lijn verbonden worden, totdat alle lijnen even lang zijn.

Dat klinkt mogelijk nogal mysterieus maar is toch niet zo moeilijk, zie figuur 2.

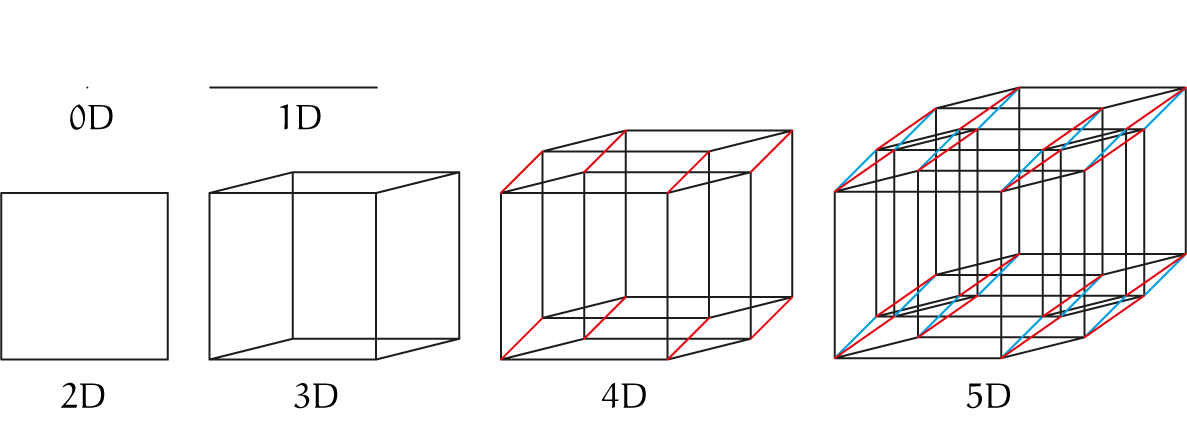
We beginnen met een punt, een '$0$-dimensionale kubus'. Volgens het voorschrift ontstaat dan een lijn met twee hoekpunten, een '$1$-dimensionale kubus'. Vervolgens een vierkant, een '$2$-dimensionale kubus', en tenslotte de echte $3D$ kubus. Om nu een $4$-dimensionale kubus te maken moeten we dus de $3$-dimensionale kubus kopiëren op zichzelf en dan één van die twee verplaatsen in de 4e dimensie. Dat is voor ons $3$-dimensionale mensen knap lastig voor te stellen, het plaatje wordt al snel complex, al helemaal voor nog meer dimensies (figuur 2, geheel rechts). Bedenk wel dat het object helemaal rechts in figuur 2 een $2D$ projectie van een $3D$ projectie van een $4D$ projectie van een $5D$ lichaam is. Oei.

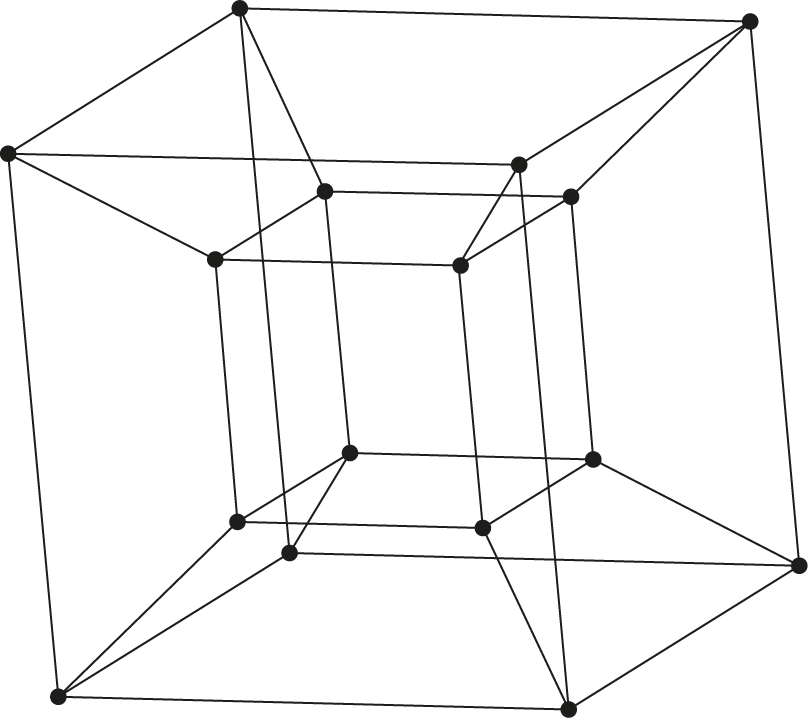
De $4$-dimensionale kubus wordt daarom vaak sterk perspectivisch weergegeven als in Figuur 3. Beschouwd als een $3D$ plaatje, wat zeer verraderlijk is, lijkt dit gewoon een kleine kubus in een grote kubus. Maar tussen twee overeenkomstige zijvlakken van die twee ligt een ruimte in de vorm van een afgeknotte piramide, zes in totaal. In feite zijn dit ook kubussen maar door de perspectivische projectie van $4D$ naar $3D$ schijnbaar vervormd. Een $4$-dimensionale kubus, ook wel tesseract geheten, bestaat dus uit acht $3$-dimensionale kubussen.

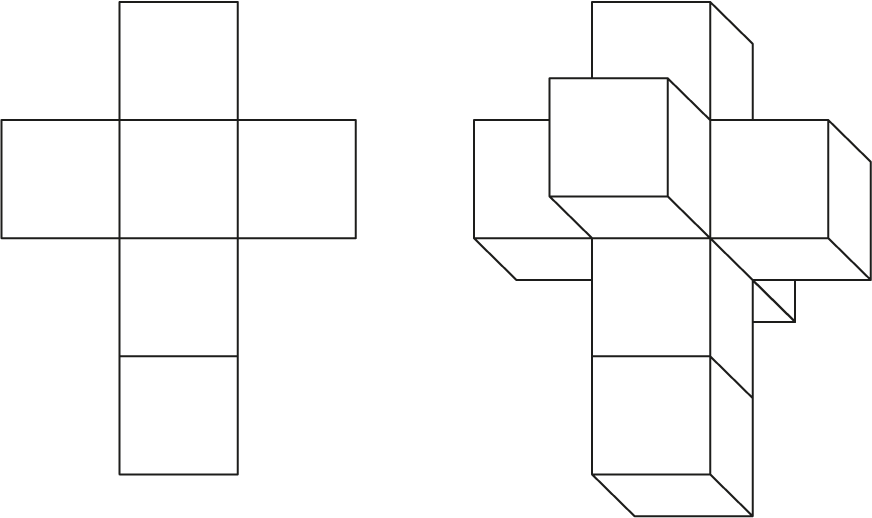
Bekijk om de situatie nog beter te aan te duiden figuur 4. Links zien we een bouwplaat van een kubus. Knip die uit en vouw de vlakken om dan ontstaat een kubus, voor de meesten onder ons die vroeger geknutseld hebben eenvoudig voor te stellen. Maar zou een $2$-dimensionaal wezen zich dat ook kunnen voorstellen? Het object daarnaast, beschouwd als een $3$-dimensionaal voorwerp, is te zien als een bouwpakket van een tesseract. We kunnen daar een echte tesseract van maken door de verschillende deelkubussen in de 4e dimensie om te vouwen en vast te plakken. Maar hoe dat moet kunnen we ons simpelweg niet voorstellen. Dat is de beperking van onze $3$-dimensionale wereld. Dus we moeten het abstract houden. Dat neemt niet weg dat de bekende science fiction schrijver Robert Heinlein hier wel een leuk verhaal over heeft geschreven: And He Built a Crooked House (1941).
Bij elke toevoeging van een extra dimensie verdubbelt het aantal hoekpunten. Tabel 1 vermeldt hoe dat met de andere delen (lijnen, vlakken, kubussen enzovoort) is, tot en met $10$ dimensies.

$N$		$H$		$R$		$V$		$3D$		$4D$		$5D$		$6D$		$7D$		$8D$		$9D$		$10D$
$0$		$1$
$1$		$2$		$1$
$2$		$4$		$4$		$1$
$3$		$8$		$12$		$6$		$1$
$4$		$16$		$32$		$24$		$8$		$1$
$5$		$32$		$80$		$80$		$40$		$10$		$1$
$6$		$64$		$192$		$240$		$160$		$60$		$12$		$1$
$7$		$128$		$448$		$672$		$560$		$280$		$84$		$14$		$1$
$8$		$256$		$1024$		$1792$		$1792$		$1120$		$448$		$112$		$16$		$1$
$9$		$512$		$2304$		$4608$		$5376$		$4032$		$2016$		$672$		$144$		$18$		$1$
$10$		$1024$		$5120$		$11520$		$15360$		$13440$		$8064$		$3360$		$960$		$180$		$20$		$1$
Tabel 1 Kenmerken van meer-dimensionale kubussen. $N$ = aantal dimensies; $H$ = aantal hoekpunten; $R$ = aantal ribben; $V$ = aantal vlakken; $3D$, $4D$, $5D$, … = aantal $3D$, $4D$, $5D$, … kubussen.

De kolom met het aantal hoekpunten is duidelijk, en ook de schuine lijn met getallen $1$ (in $N$ dimensies slechts één $N$-dimensionaal object). Voor de andere vakjes blijkt er nu een simpele recurrente betrekking tussen de verschillende vakjes te bestaan. Zie het schema in figuur 5 voor drie aangrenzende vakjes in de tabel, dan geldt voor de kubus: $C = A + 2B$.

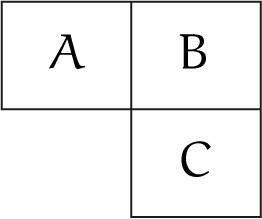
Hiermee kan bijvoorbeeld in een spreadsheet
eenvoudig de tabel worden gemaakt. Uit deze tabel blijkt dat bij toenemend aantal dimensies de zaak snel gecompliceerd wordt, en een simpele schematische weergave van het object is nagenoeg onmogelijk.

De coördinaten van de hoekpunten van een meerdimensionale kubus zijn: $(\pm a, \pm a,
\pm a, \ldots)$ waarbij $a$ de halve lengte van een
ribbe is. Dus voor een eenheidskubus met
ribbe lengte $1$ is $a = \tfrac{1}{2}$. De kleinste afmeting is die in de richting van één van de assen, of anders gezegd: evenwijdig aan een ribbe, en voor de eenheidskubus is die altijd $1$. De grootste afmeting is de afstand tussen twee diametraal tegenover elkaar gelegen hoekpunten en die is waarbij $N$ het aantal
dimensies is.

De inhoud (volume) van een eenheidskubus is altijd $1$. Het 'oppervlak' is de som van de afmetingen van de begrenzende objecten, en dat is gelijk aan het aantal $(N - 1)$-dimensionale objecten (ieder met 'volume' $1$), in tabel 1 het getal steeds links van de $1$. Dat is dus $2N$.

Andere Platonische lichamen

$De\ octa\ddot{e}der$

De octaëder (regelmatig achtvlak) is wat complexer van vorm dan de kubus. Er is ook een voorschrift om ze te construeren net als bij de kubus, maar die is wat cryptisch.

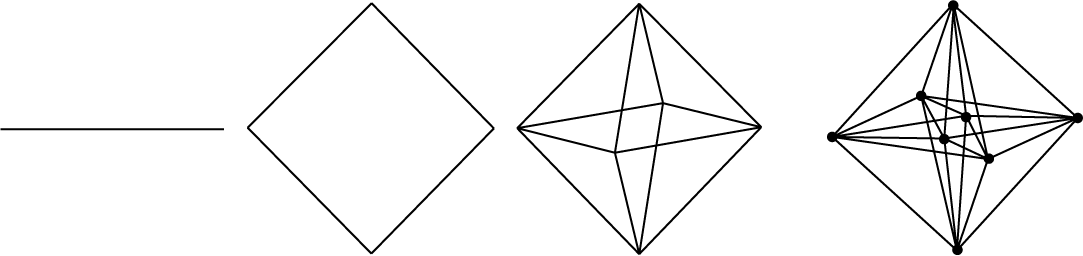
Plaats twee nieuwe punten midden in het lichaam, verbind die met alle hoekpunten maar niet met elkaar; verplaats nu deze twee punten in de richting van de nieuwe dimensie maar tegengesteld totdat alle lijnen even lang zijn; verwijder het oorspronkelijke lichaam.

De laatste opmerking is merkwaardig, maar zie figuur 6.  Bij de overgang van $1D$ naar $2D$ (lijn naar vierkant) moet de oorspronkelijke lijn vervallen, en bij de overgang van $2D$ naar $3D$ moet het oorspronkelijk vierkante vlak vervallen (de lijnen blijven wel staan!).

De $4D$ figuur lijkt gewoon een octaëder met twee extra punten daarin. Maar dat is schijn, in werkelijkheid ($4D$!!) liggen de punten er buiten. Met enige moeite kunnen we zien dat de $4D$ octaëder niet is opgebouwd uit $3D$ octaëders, maar uit $3D$ tetraëders, en dat geldt ook voor nog meer dimensies. In feite geldt dat ook al voor de $3D$ octaëder die strikt genomen is opgebouwd uit ‘$2D$-tetraëders’ (lees: driehoeken).

Uit het voorschrift volgt dat bij elke nieuwe dimensie het aantal hoekpunten met $2$ vermeerdert. De andere gegevens zijn in tabel 2 te vinden. Ook hier geldt een simpele recurrente betrekking (figuur 5):

$$C = 2A + B$$

met uitzondering van de getallen direct links van de $1$.

De $3D$ kubus en octaëder zijn aan elkaar verwant: de middelpunten van de vlakken van de ene zijn de hoekpunten van de andere. Dit gaat ook op voor meer dimensie en dat blijkt uit een vergelijk van de tabellen 1 en 2: de getallen op overeenkomstige rijen zijn gespiegeld.

De coördinaten van de $2N$ hoekpunten van een meerdimensionale octaëder zijn: $(\pm a, 0, 0, \cdots)$, $(0, \pm a, 0, \cdots)$,  $(0, 0, \pm a, \cdots), \cdots$, en de omhulling wordt gegeven door de vergelijking  $|x_1| + |x_2| + |x_3| + \cdots = a$. Voor een eenheidsoctaëder met ribbe lengte $1$ is $a$ gelijk aan $\tfrac{1}{2}\sqrt{2}$. Er zijn dus $2^N$ combinaties van $N$ hoekpunten; en dat zijn precies de hoekpunten van de $2^N$ $(N-1)$-dimensionale tetraëders waaruit de octaëder is opgebouwd.

Opmerkelijk is nu dat twee diametraal tegenover elkaar liggende hoekpunten altijd een afstand hebben van $\sqrt{2} \times $ de ribbe lengte, ongeacht het aantal dimensies.

$N$		$H$		$R$		$V$		$3D$		$4D$		$5D$		$6D$		$7D$		$8D$		$9D$		$10D$
$0$		$1$
$1$		$2$		$1$
$2$		$4$		$4$		$1$
$3$		$6$		$12$		$8$		$1$
$4$		$8$		$24$		$32$		$16$		$1$
$5$		$10$		$40$		$80$		$80$		$32$		$1$
$6$		$12$		$60$		$160$		$240$		$192$		$64$		$1$
$7$		$14$		$84$		$280$		$560$		$672$		$448$		$128$		$1$
$8$		$16$		$112$		$448$		$1120$		$1792$		$1792$		$1024$		$256$		$1$
$9$		$18$		$144$		$672$		$2016$		$4032$		$5376$		$4608$		$2304$		$512$		$1$
$10$		$20$		$180$		$960$		$3360$		$8064$		$13440$		$15360$		$11520$		$5120$		$1024$		$1$
Tabel 2 Kenmerken van meer-dimensionale octaëders. Betekenis als in tabel 1, zij het dat de lichamen nu octaëders èn tetraëders zijn (zie tekst)

Het ‘volume’ van een $N$-dimensionale octaëder met ribbe lente $1$ is gelijk aan (verdere uitleg staat bij "Oplossingen" onderaan):

$$V=\frac{\sqrt{2^N}}{N!}.$$

De waarden zijn te vinden in tabel 3. De waarde voor $N=1$ heeft geen praktische betekenis.

$N$		$0$		$1$		$2$		$3$		$4$		$5$		$6$		$7$		$8$		$9$		$10$
$vol$		$1$		$1{,}414$		$1$		$0{,}471$		$0{,}167$		$0{,}0471$		$0{,}0111$		$2{,}25\cdot 10^{-3}$		$3{,}97\cdot 10^{-4}$		$6{,}24\cdot 10^{-5}$		$8{,}82\cdot 10^{-6}$
Tabel 3 'Volume' van $N$-dimensionale octaëders met ribbe lengte $1$

$De\ tetra\ddot{e}der$

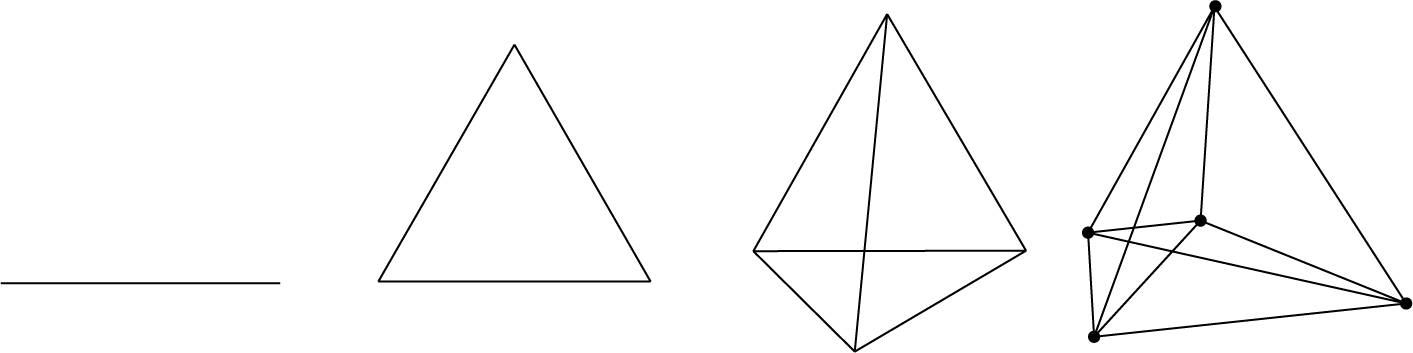
Vergeleken met de kubus en de octaëder is de tetraëder (regelmatig viervlak) maar een simpel ding. Het voorschrift om een dimensie toe te voegen luidt:

Plaats een nieuw punt midden in het lichaam, verbind die met alle hoekpunten, en verplaats dit punt in de richting van de nieuwe dimensie totdat alle lijnen even lang zijn.

Dat is alles, zie figuur 7. Ook hier lijkt de $4D$ figuur gewoon een tetraëder met een extra punt er in. Maar in werkelijkheid ($4D$!!) ligt dat punt erbuiten. En we kunnen ook zien dat de $4D$ tetraëder is opgebouwd uit $3D$ tetraëders.

$N$		$H$		$R$		$V$		$3D$		$4D$		$5D$		$6D$		$7D$		$8D$		$9D$		$10D$
$0$		$1$
$1$		$2$		$1$
$2$		$3$		$3$		$1$
$3$		$4$		$6$		$4$		$1$
$4$		$5$		$10$		$10$		$5$		$1$
$5$		$6$		$15$		$20$		$15$		$6$		$1$
$6$		$7$		$21$		$35$		$35$		$21$		$7$		$1$
$7$		$8$		$28$		$56$		$70$		$56$		$28$		$8$		$1$
$8$		$9$		$36$		$84$		$126$		$126$		$84$		$36$		$9$		$1$
$9$		$10$		$45$		$120$		$210$		$252$		$210$		$120$		$45$		$10$		$1$
$10$		$11$		$55$		$165$		$330$		$462$		$462$		$330$		$165$		$55$		$11$		$1$
Tabel 4 Kenmerken van meer-dimensionale tetraëders. Betekenis als in tabel 1, zij het dat de lichamen nu tetraëders zijn

Het aantal hoekpunten neemt dus bij elke extra dimensie slechts met één toe. De rest staat in tabel 4. Ook hier geldt een simpele recurrente betrekking (figuur 5):

$$C = A + B.$$

Als we de grootte van de getallen vergelijken met de tabellen 1 en 2 blijkt ook weer dat de tetraëder veel simpeler is.

De tetraëder is zijn eigen verwante: de middelpunten van de vlakken zijn de hoekpunten van weer een tetraëder. Ook dat blijkt uit de tabel: de getallen in de rijen zijn symmetrisch, en gelijk  aan de getallen uit de driehoek van Pascal; een direct gevolg van de recurrente betrekking.

Door het gemis van symmetrie zijn de hoek-coördinaten van de tetraëder niet zo eenvoudig uit te drukken als bij de kubus en de octaëder, maar er is wel een systeem, zie tabel 5 (zie "Oplossingen"); de getallen $1, 3, 6, 10, 15, 21$ enz. zijn de zogenaamde driehoeksgetallen. De dikke lijnen geven de begrenzingen aan van de coördinaten van resp. $1-$ , $2-$ , $3-$ , $4-$, $5-$ en $6-$dimensionale tetraëders; er is altijd één hoekpunt meer dan het aantal dimensies.

		$1$		$2$		$3$		$4$		$5$		$6$		$7$
$x_1$		$-1$		$1$		$0$		$0$		$0$		$0$		$0$
$x_2$		$-\sqrt{\tfrac13}$		$-\sqrt{\tfrac13}$		$2\sqrt{\tfrac13}$		$0$		$0$		$0$		$0$
$x_3$		$-\sqrt{\tfrac16}$		$-\sqrt{\tfrac16}$		$-\sqrt{\tfrac16}$		$3\sqrt{\tfrac16}$		$0$		$0$		$0$
$x_4$		$-\sqrt{\tfrac{1}{10}}$		$-\sqrt{\tfrac{1}{10}}$		$-\sqrt{\tfrac{1}{10}}$		$-\sqrt{\tfrac{1}{10}}$		$4\sqrt{\tfrac{1}{10}}$		$0$		$0$
$x_5$		$-\sqrt{\tfrac{1}{15}}$		$-\sqrt{\tfrac{1}{15}}$		$-\sqrt{\tfrac{1}{15}}$		$-\sqrt{\tfrac{1}{15}}$		$-\sqrt{\tfrac{1}{15}}$		$5\sqrt{\tfrac{1}{15}}$		$0$
$x_6$		$-\sqrt{\tfrac{1}{21}}$		$-\sqrt{\tfrac{1}{21}}$		$-\sqrt{\tfrac{1}{21}}$		$-\sqrt{\tfrac{1}{21}}$		$-\sqrt{\tfrac{1}{21}}$		$-\sqrt{\tfrac{1}{21}}$		$6\sqrt{\tfrac{1}{21}}$
Tabel 5 Coördinaten van de hoekpunten van tetraëders met ribbe lengte $2$, t/m $6$ dimensies. kolom 1 t/m.7: nummer hoekpunt); $x_1, x_2, \cdots, x_6$: coördinaat

Het ‘volume’ van een N-dimensionale tetraëder met ribbe lente 1 is gelijk aan (zie "Oplossingen"): $$V=\frac{\sqrt{N+1}}{N!\sqrt{2^N}}.$$

Bij toenemend aantal dimensies wordt het volume dus snel heel klein (tabel 6).

$N$		$0$		$1$		$2$		$3$		$4$		$5$		$6$		$7$		$8$		$9$		$10$
$vol$		$1$		$1$		$0{,}433$		$0{,}118$		$0{,}0233$		$3{,}61\cdot 10^{-3}$		$4{,}59\cdot 10^{-4}$		$4{,}96\cdot 10^{-5}$		$4{,}65\cdot 10^{-6}$		$3{,}85\cdot 10^{-7}$		$2{,}86\cdot 10^{-8}$
Tabel 6 'Volume' van $N$-dimensionale tetraëders met ribbe lengte $1$

 

$Andere\ lichamen$

Het is ook mogelijk om het twaalfvlak (dodecaëder) en het twintigvlak (icosaëder) uit te breiden naar vier dimensies, maar dat is verre van simpel. Voor een $4D$-twaalfvlak zijn maar liefst $120$ $3D$-twaalfvlakken nodig, en voor een $4D$ twintigvlak zelfs $600$ $3D$-tetraëders. Dus dat laten we maar voor wat het is.

De bol

Een bol is wel extreem simpel. Er zijn geen hoekpunten, geen lijnen, geen vlakken, niets van dat alles, alleen een bol met als omhulling het bekende: $x^2_1 + x^2_2 + \cdots + x^2_N = r^2$. Maar het berekenen van bijvoorbeeld het
volume van een bol is wel wat ingewikkelder, het is nog wel stof voor VWO 5 en 6. In het volgende definiëren we het volume van een $N$-dimensionale bol als: $V_Nr^N$; in feite is dus $V_N$ het volume van een $N$-dimensionale bol met straal $1$. We weten nog wel dat $V_2 = \pi$ en als het goed is ook dat $V_3 = 4\pi/3$.

Bekijk nu figuur 8. Daarin is een cirkel
afgebeeld met middelpunt $M$ en straal $1$. Bij punt $A$ op een afstand $h$ van $M$ wordt de cirkel doorsneden door de lijn $BC$ met $AB=r=\sqrt{1-h^2}$. We kunnen nu het
oppervlak van de cirkel uitrekenen door punt $A$ over de hele hoogte van de cirkel
te schuiven $(-1 \le h \le 1)$ en alle lengtes
$BC (= 2r)$ bij elkaar op te tellen. Dat heet
integreren. Dus:

$$O=V_2=\int^1_{-1}2r{\rm d}h=2\int^1_{-1}r{\rm d}h (= \pi).$$

Maar we kunnen de cirkel ook beschouwen als een doorsnede door een bol (door het middelpunt). Bij punt $A$ wordt de bol dan doorsneden door een vlak, en de doorsnede is een cirkel met straal $r$ en oppervlak $\pi r^2$.

Het volume van de bol is dan een integraal
van alle doorsnedes:

$$V=V_3=\int^1_{-1}\pi r^2{\rm d}h=\pi\int^1_{-1}r^2{\rm d}h=V_2\int^1_{-1}r^2{\rm d}h.$$

Deze lijn doortrekkende kunnen we nu in het algemeen stellen dat:

$$V_{N+1}=V_N\int^1_{-1}r^N{\rm d}h.$$

Dat confronteert ons echter met de uitdrukking $r^N=\left(\sqrt{1-h^2}\right)^N=\left(1-h^2\right)^{N/2}$. Voor even waarden van $N$ is de berekening nog wel te doen maar voor oneven waarden van $N$ is het lastig. Gelukkig komt het handboek ons te hulp:

$$\int^1_{-1}r^N{\rm d}h=\int^1_{-1}\left(1-h^2\right)^{N/2}{\rm d}h=\frac{2^{N+1}}{(N+1)!}\left\{\Gamma\left(\frac{N}{2}+1\right)\right\}^2=F_N$$

dus $V_{N+1} = V_N F_N$. De niet zo bekende $\Gamma$ (gamma) functie is in feite een continu equivalent van de faculteitsfunctie; voor hele waarden van $N > 0$ geldt: $\Gamma(N)=(N-1)!$ waaruit meteen volgt dat $\Gamma(1) = 0! = 1$. Verder is het hier voldoende om te weten dat $\Gamma(x+1)=x\Gamma(x)$ en $\Gamma\left(\tfrac{1}{2}\right)=\sqrt{\pi}$.

$N$

$0$

$1$

$2$

$3$

$4$

$5$

$6$

$7$

$8$

$9$

$10$

$V_N$

$1$

$2$

$\pi$

$4\pi/3$

$\pi^2/2$

$8\pi^2/15$

$\pi^3/6$

$16\pi^3/105$

$\pi^4/24$

$32\pi^4/945$

$\pi^5/120$

$O_N$

$2$

$2\pi$

$4\pi$

$2\pi^2$

$8\pi^2/3$

$\pi^3$

$16\pi^3/15$

$\pi^4/3$

$32\pi^4/105$

$\pi^5/12$

Tabel 7 'Volume' $V_N$ en 'oppervlakte' $O_N$ van een $N$-dimensionale bol met straal $1$

Het is nu gewoon een kwestie van stug doorrekenen, de uitkomsten staan in tabel 2; bedenk wel dat de waarde voor $V_0$ geen echte betekenis heeft. Uit de tabel blijkt dus bijvoorbeeld dat het 'volume' van een $5$-dimensionale bol gelijk is aan

$$V_5r^5=\frac{8}{15}\pi^2r^5.$$

Met name de uitdrukkingen voor oneven $N$ zijn nou niet bepaald om blij van te worden. Opmerkelijk is nu dat uit deze resultaten een heel eenvoudige recurrente betrekking opduikt die in één klap alle moeizame berekeningen overbodig maakt: $$V_0 = 1; V_1 = 2; V_N = V_{N-2}2\pi/N.$$

Deze betrekking kan ook direct worden afgeleid maar dat is niet zo simpel.

Uit deze betrekking valt eenvoudig te zien dat voor waarden van $N$ groter dan $6$ de waarden van $V_N$ steeds kleiner worden. Dit blijkt nog meer uit tabel 3 waar de numerieke waarden voor $V_N$ zijn gemeld. Voor veel dimensies lijkt de waarde van $V_N$ zelfs zeer klein.

$N$

$1$

$2$

$3$

$4$

$5$

$6$

$7$

$8$

$9$

$10$

$V_N$

$2$

$3{,}142$

$4{,}189$

$4{,}935$

$5{,}264$

$5{,}168$

$4{,}725$

$4{,}059$

$3{,}299$

$2{,}55$

$V_{N+10}$

$1{,}884$

$1{,}335$

$0{,}911$

$0{,}599$

$0{,}381$

$0{,}235$

$0{,}141$

$0{,}0821$

$0{,}0466$

$0{,}0258$

$V_{N+20}$

$0{,}014$

$0{,}007$

$0{,}004$

$0{,}002$

$0{,}00096$

$0{,}00047$

$0{,}00022$

$0{,}00011$

$0{,}000048$

$0{,}000022$

Tabel 8 Numerieke waarden voor het 'volume' $V_N$ van een $N$-dimensionale bol met straal $1$

Het oppervlak van de $N$-dimensionale bol is nu simpel te bepalen, immers $O = {\rm d}V/{\rm d}r$. Dus als het volume is $V_N r^N$ dan is het oppervlak $N V_N r^{N-1}$, dus kunnen we zeggen dat $O_N = NV_N$; de waardes zijn volledigheidshalve ook in tabel 2 vermeld. Maar het is praktischer om de oppervlakte van een $N$-dimensionale bol te vergelijken met die van een $N$-dimensionale eenheidskubus, en we hebben al eerder gezien dat die laatste gelijk is aan $2N$. Dat levert voor het relatieve oppervlak op $O^\prime_N = V_N/2$.

Maar er is een groot mysterie. Stel voor een $N$-dimensionale bol met straal $1$ met daarin in het midden een $N$-dimensionale eenheidskubus (met ribbe $1$). Bij twee dimensies (cirkel met vierkant) en drie dimensies (bol
met kubus) ligt de 'kubus' helemaal in de 'bol'. Maar bij vier dimensies is de hoek-hoek afstand in de kubus $2$, dus gelijk aan de diameter van de bol. Dat betekent dat alle hoekpunten van de kubus op de bol liggen. Bij vijf en meer dimensies prikken de hoekpunten van de kubus zelfs door de bol heen, en des te meer naargelang er meer dimensies zijn. Je kunt dan stellen dat de bol steeds kleiner wordt ten opzichte van de kubus, en dat bevestigen de getallen in tabel 3, bedenk dat het volume van een eenheidskubus altijd $1$ is. De bol wordt zelfs in verhouding belachelijk klein, en je verwacht dat die wel helemaal in de kubus ligt. Maar dat is niet zo. De afmetingen van
de kubus in de richting van een as is altijd $1$, terwijl de diameter van de bol $2$ is, en die is dus groter.

Dus de belachelijk kleine bol ligt toch nog gedeeltelijk buiten de kubus! Dus moet die bol naar ons idee wel een krankzinnige vorm hebben, maar dat is niet zo: het is en blijft een gewone, zij het meerdimensionale, ronde bol. Dat is niet voor te stellen, en het bevestigt de opvatting dat wij als $3$-dimensionale wezens ons helemaal geen voorstelling kunnen maken van een wereld met meer dan drie dimensies. Maar ze kunnen desalniettemin wiskundig wel bestaan.

Bijlagen

Verdere uitleg over coördinaten van tetraëders, volumes vna octaëders en tetraëders en de afleiding van de recurrente betrekking voor bolvolumes kun je vinden via de knop [Bekijk oplossing] hieronder.

 

Bekijk oplossing