Om beter gevoel te krijgen voor het goed gespreid inruimen van de vaatwasser had Pi besloten eerst te onderzoeken hoe je punten één voor één handig op een cirkel kan plaatsen, zodanig dat de spreiding op elk moment zo goed mogelijk is. Het eerste punt plaatsen is makkelijk: vanwege de symmetrie van de nog lege cirkel zijn alle plaatsen even goed. Maar dan. Een recept zou kunnen zijn om elk volgende punt in het midden van een langste boog zonder punten te plaatsen. Laten we de plaats van een punt aanduiden met de hoek t.o.v. het eerste punt gemeten als fractie van $360^{\rm o}$ (tegen de klok is positief). Dan komen de punten met dat recept op oneven veelvouden van negatieve machten van twee: $(2k+1)2^{-n}$.

Er zijn dan altijd (lege) bogen van maximaal twee lengtes, waarbij de lange boog twee keer zo lang is als de korte. Telkens wordt een lange boog gehalveerd. Dat lijkt niet slecht, maar het kan beter, d.w.z. dat we een kleinere gemiddelde verhouding tussen de lange en korte boog kunnen realiseren.

Beschouw daartoe het volgende recept met parameter $a$.

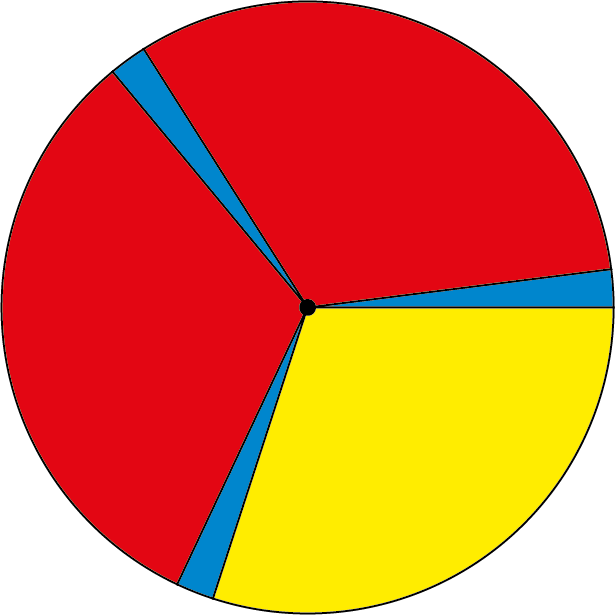
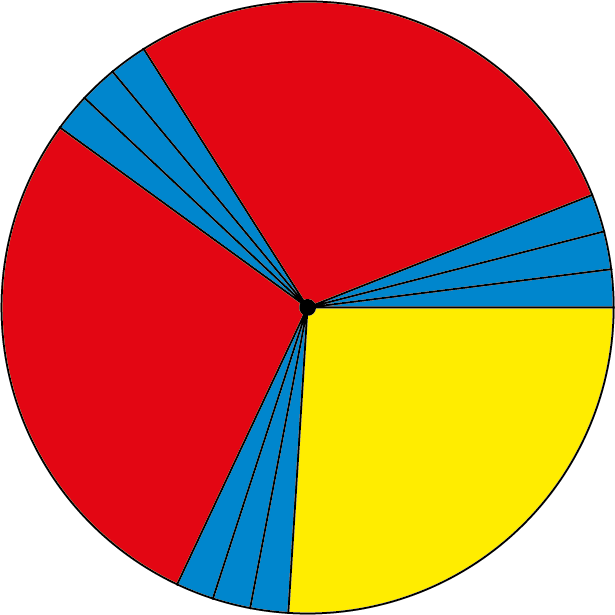
Zet het $k$-de punt op de plaats met hoekfractie $(k - 1)a$ waarbij we een fractie groter dan $1$ reduceren door het gehele deel weg te laten. We kunnen die $a$ in dit recept nog kiezen. Als a echter een breuk is, zeg $p/q$, dan valt het $q$-de punt zeker samen met het eerste punt en dat willen we natuurlijk niet. We moeten voor $a$ dus een irrationaal getal kiezen, zoals $\pi/10 \approx 0{,}314$. Verrassend genoeg blijkt het dat bij dit recept er maar hooguit drie booglengtes optreden (zoek maar eens naar Three-Gap Theorem). Elk volgend punt komt in een langste (lege) boog terecht en deelt dit in de twee kortere booglengtes. Voor $a \approx 3,4$ zien we in figuur 1 dat er bij plaatsing van $6$ punten duidelijk een clustering optreedt: er zijn drie clubjes van twee punten die dicht bij elkaar liggen, terwijl de clubjes zelf behoorlijk ver uit elkaar liggen. Dat komt omdat $0{,}34$ dicht bij $\tfrac{1}{3}$ ligt. Bij $12$ punten zijn er nog steeds drie clubjes, nu elk met vier punten (zie figuur 2). De vraag die nog rest is wat de beste keuze voor $a$ is. Dat blijkt de inverse van de gulden snede te zijn: $1/\varphi \approx 0{,}618$, of het complement $1 - 1/\varphi ≈ 0,382$. figuur 3 toont hoe $24$ punten dan verdeeld worden. De gulden snede is een irrationaal getal dat zich heel slecht laat benaderen door een breuk. De natuur heeft dat ook "ontdekt", bijvoorbeeld bij het plaatsen van bladeren aan stengels en van zaadjes op een zonnebloem.