De eerste brief is van 29 november 1873. Hierin stelde Cantor de volgende vraag aan Dedekind.

Halle, d. 29^ten Nov. 73.

Man nehme den Inbegriff aller positiven ganzzahligen Individuen $n$ und bezeichne ihn mit $(n)$; ferner denke man sich etwa den Inbegriff aller positiven reellen Zahlgrössen $x$ und bezeichne ihn mit $(x)$; so ist die Frage einfach die, ob sich $(n)$ dem $(x)$ so zuordenen lasse, dass zu jedem Individuum des einen Inbegriffes ein und nur eines des andern gehört?

Voor wie niet zo goed is in het Duits zal ik uitleggen wat hier staat. Cantor begint met twee verzamelingen te benoemen. De eerste is gewoon de verzameling der natuurlijke getallen; de notatie, $(n)$, is niet die wij nu gebruiken (wij schrijven $\mathbb{N}$). De tweede bestaat uit alle positieve reële getallen en in plaats van Cantors notatie $(x)$ schrijven wij nu wel eens $(0, \infty)$, of $(0, \rightarrow)$, of $\mathbb{R}_{+}$ .

Daarna komt het, de vraag die alles in werking zette: kunnen we de elementen van $(n)$ en van $(x)$ zó aan elkaar koppelen dat bij elk element van de ene verzameling precies één element van de andere hoort, en dat beide kanten op?

Hier werd eigenlijk van twee oneindige verzamelingen, $\mathbb{N}$ en $(0, \infty)$, gevraagd of ze ‘evenveel elementen’ hebben. Het bijzondere was dat Cantor niet tevreden was met “ze hebben allebei oneindig veel elementen, dus ja”. Hij wilde echt de verzamelingen één op één aan elkaar koppelen.

Twee pakken hagelslag

Stel je eens voor dat je twee pakken chocoladehagel hebt en je wilt weten of er evenveel korrels in de pakken zitten. Nu kun je gaan zitten tellen maar dat duurt lang en als je afgeleid wordt raak je misschien de tel kwijt. Het kan handiger: koppel telkens één korrel uit het ene pak aan één uit het andere – en eet ze op, dan weet je zeker dat ze niet dubbel gekoppeld worden.

Het duurt even maar als de pakken tegelijk leeg zijn dan weet je dat er evenveel korrels in beide pakken zaten en anders weet je welk pak meer korrels bevatte.

Als je dit na wilt spelen zou ik twee van die kleine doosjes nemen die je wel in hotels op de ontbijttafel ziet; dan duurt het niet zo lang.

Bij oneindige verzamelingen is dit niet praktisch want je bent dan oneindig lang bezig. Wat je hier nodig hebt is óf een formule (en die mag best ingewikkeld zijn) die een koppeling beschrijft, óf een bewijs dat zo’n koppeling niet bestaat.

Voor we naar de tweede brief gaan kijken, waarin Cantor zelf zijn vraag beantwoordde, zou je eens kunnen nadenken hoe je zelf zoiets zou aanpakken.

Wat denk je? Bestaat er zo’n koppeling, of niet?

Tussen de twee brieven

De post werkte vrij efficiënt in die tijd want reeds op 2 december beantwoordde Cantor een brief van Dedekind waarin deze had geschreven dat hij geen antwoord had op de vraag. Wat de twee wel hadden vastgesteld was dat er een koppeling bestaat tussen de natuurlijke getallen en de algebraïsche getallen, dat zijn de reële getallen die oplossing zijn van een vergelijking van de vorm

$$a_0 + a_1 x + a_2 x^2 + … + a_n x^n = 0$$

waarbij alle coëfficiënten gehele getallen zijn. En dus, schreef Cantor, zou een negatief antwoord op zijn vraag een nieuw bewijs betekenen van een stelling van Liouville, die zegt dat er (heel veel) niet-algebraïsche getallen bestaan.

Breuken

Dat koppelen van die algebraïsche getallen aan de natuurlijke getallen is wat ingewikkeld maar de manier waarop Cantor het later opschreef lijkt in de verte op het volgende. Neem de positieve breuken. Bepaal voor elke breuk $t/n$ de som van teller en noemer: $t + n$. Bij een vast natuurlijk getal $m$ zijn er precies $m$ breuken waarvoor die som gelijk is aan $m + 1$, namelijk, $\frac{1}{m}, \frac{2}{m-1},…, \frac{m}{1}$.

Nu gaat het koppelen als volgt: sorteer de breuken eerst naar de som van teller en noemer en zet ze per vaste som in hun normale volgorde.

Probeer zelf eens formules te bedenken die aangeven aan welk natuurlijk getal de breuk $t/n$ gekoppeld is, en aan welke breuk een natuurlijk getal $m$ gekoppeld is.

De tweede brief

Op 7 december 1873 schreef Cantor alweer een brief, nu met de oplossing van zijn probleem: hij had bewezen dat er geen koppeling bestaat. Of eigenlijk: hij was wat voorzichtiger, hij schreef dat hij hoopte dat het bewijs in de brief correct was. Dat kunnen we zelf controleren want hier komt het.

Het bewijs was uit het ongerijmde: stel er is een koppeling tussen de natuurlijke getallen en alle reële getallen in het interval $\langle 0, 1 \rangle$. Dan kunnen we die getallen op een rij zetten:

$$\omega_1, \omega_2, \omega_3, …, \omega_\nu, ...$$

We gaan die rij in deelrijen verdelen; dat vergt wat notatie en het is wel handig als je met pen en papier meewerkt.

Terzijde: in het bewijs is het niet nodig dat je de reële getallen als echte getallen beschouwt. Het enige dat van belang is dat ze op een lijn liggen en dat in die lijn geen gaten zitten. Cantor had dus ook kunnen zeggen: stel er is een koppeling tussen de natuurlijke getallen en alle punten op een lijnstuk (van lengte $1$). Het maakt voor het bewijs niets uit.

De eerste deelrij maken we als volgt: noteer $\omega_{1,1} = \omega_1$, dan is er een eerste $k > 1$ met $\omega_k > \omega_{1,1}$, noteer $\omega_{1,2} = \omega_k$ (de $2$ is een index), dan is er een eerste $l > k$ met $\omega_l > \omega_{1,2}$, noteer $\omega_{1,3} = \omega_l$. Zo krijgen we dus een stijgende rij

$$\omega_{1,1}, \omega_{1,2}, \omega_{1,3}, …, \omega_{1,\nu}, ...$$

Kun je uitleggen waarom die rij oneindig lang doorloopt?

De natuurlijke getallen $1, k, l, ...$ die we zijn tegengekomen leggen we terzijde. Van de overgebleven natuurlijke getallen nemen we het minimum, zeg $m$ en we maken een nieuwe rij

$$\omega_{2,1}, \omega_{2,2}, \omega_{2,3}, …, \omega_{2,\nu}, ...$$

Begin met $\omega_{2,1}= \omega_m$ en neem telkens, als je $\omega_{2,\nu}$ bepaald hebt het eerste van de overgebleven natuurlijke getallen, zeg $n$, met $\omega_n > \omega_{2,\nu}$ en noteer $\omega_{2,\nu+1} = \omega_n$.

Blijf dit herhalen: als je $k$ rijen gemaakt hebt maak dan de volgende

$$\omega_{k+1,1}, \omega_{k+1,2}, \omega_{k+1,3}, … , \omega_{k+1,\nu}, ...$$

op precies dezelfde manier: begin met $\omega_{k+1,1} = \omega_m$ waar $m$ het eerste natuurlijke getal is dat nog niet gebruikt is en $\omega_{k+1,\nu+1}$ telkens de eerste nog niet gebruikte term in de rij is die groter is dan $\omega_{k+1,\nu}$ .

Wat voor straks belangrijk is is dat elke term van de oorspronkelijke rij meegenomen wordt: $\omega_1$ zit in de eerste rij; als $\omega_2$ niet in de eerste rij is gestopt dan komt hij in de tweede rij, omdat we altijd de eerste niet-gebruikte term nemen; zo zien we ook dat $\omega_3$ in een van de eerste drie rijen moet zitten; $\omega_4$ in een van de eerste vier, enzovoort.

Neem nu het open interval $\langle \omega_{1,1},\omega_{1,2}\rangle$; daar zit geen enkele term van de eerste rij in, we noteren dit interval als $(p_1,q_1)$.

Bekijk nu de tweede rij; het kan zijn dat geen enkele term van die rij in $(p_1,q_1)$ zit, dat is prima. Het kan zijn dat er ook geen term van de derde rij in $(p_1,q_1)$ zit, dat is ook niet erg. Maar omdat onze beginrij een koppeling is komt er een eerste $k$ (en $k = 2$ is mogelijk) met een eerste $\nu$ zó dat $\omega_{k,\nu} \in \langle p_1,q_1 \rangle$. Dan schrijven we $p_2 = \omega_{k,\nu}$ en we nemen $q_2$ tussen $p_1$ en $\min\{q_1,\omega_{k,\nu+1}\}$ (bijvoorbeeld het gemiddelde van die twee). In het volgende plaatje is het interval $\langle p_1,q_1 \rangle$ wat uitvergroot; het toont de situatie met $\omega_{k,\nu} < q_1 < \omega_{k,\nu+1}$ .

 

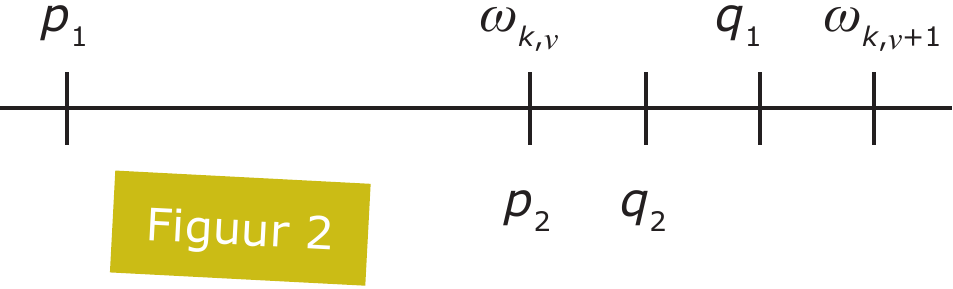
Waarom? Omdat we zo een interval $\langle p_2,q_2 \rangle$ krijgen met $p_1 < p_2 < q_2 < q_1$ (dat is belangrijk voor straks) en zó dat geen enkele term van de eerste $k$ rijen in het interval zit. In het bijzonder zitten dus $\omega_1$ tot en met $\omega_k$ niet in $\langle p_2,q_2 \rangle$.

Nu kijken we naar $\langle p_2,q_2 \rangle$ en nemen de eerste $l > k$ en de eerste $\mu$ met $\omega_{l,\mu} \in \langle p_2,q_2 \rangle$. Dan schrijven we $p_3 = \omega_{k,\nu}$ en we nemen $q_3$ tussen $p_2$ en $\min\{q_2,\omega_{l,\mu+1}\}$.

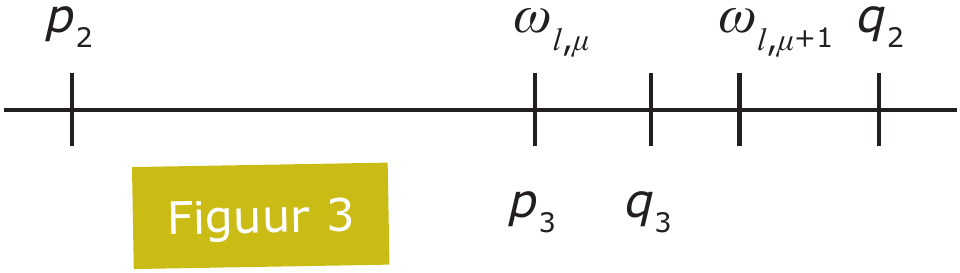
Zo krijgen we een rij intervallen met de volgende eigenschappen. Voor elke $k$ geldt $p_k < p_{k+1} < q_{k+1} < q_k$ en voor elke $k$ geldt dat $\omega_1$ tot en met $\omega_k$ niet in het interval $\langle p_k,q_k \rangle$ zitten.

Omdat in de getallenlijn geen gaten zitten is er een getal $\eta$ zó dat $p_k < \eta < q_k$ voor alle $k$.

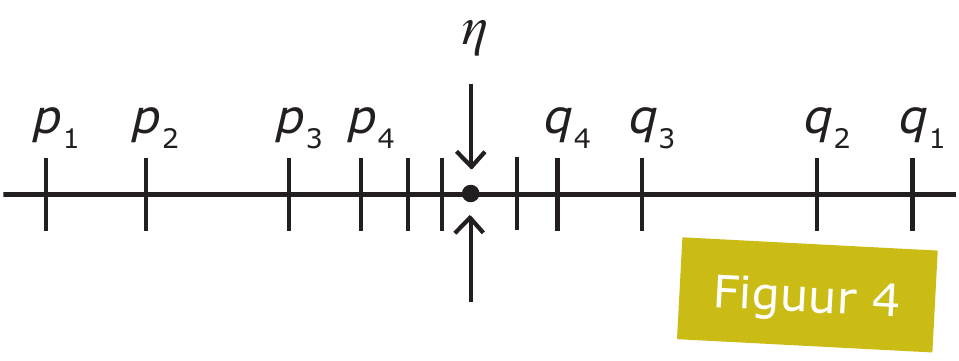
Maar dan hebben we een tegenspraak gevonden: $\eta \neq \omega_k$ voor alle $k$; dus de koppeling was toch geen koppeling.

Aan het eind schreef Cantor: Ik geloof dat ik nu eindelijk doorgrond heb waarom de verzameling die ik eerder met $(x)$ noteerde zich niet eenduidig aan de met $(n)$ aangegeven verzameling laat koppelen.

Waarom was dit nu zo bijzonder? Omdat voor het eerst een echt onderscheid was gemaakt tussen twee soorten oneindigheid. Hierboven hadden we al gezien dat Cantor niet tevreden was met “$(n)$ en $(x)$ zijn beide oneindig”; hij wilde weten of er een echt verschil was.

Cantor ging door met zijn onderzoek. Een paar jaar later bewees hij dat het interval $[0,1]$ en het vierkant $[0, 1] \times [0, 1]$ evenveel punten hebben: hij wist op een mooie manier een koppeling tussen die twee verzamelingen te maken. Ook bleef hij zijn leven lang op zoek naar een bewijs van de volgende bewering: als $X$ een oneindige deelverzameling van $\mathbb{R}$ is dan is er een koppeling tussen $X$ en de natuurlijke getallen of een koppeling tussen $X$ en de reële getallen. Dat is hem (en anderen) niet gelukt en in 1963 bleek waarom: zo’n bewijs is er niet. Dat wil niet zeggen dat de bewering fout is want in 1940 was al aangetoond dat je het tegendeel van de bewering niet kunt bewijzen. Voor wie wil weten hoe dat in zijn werk gaat, een bewering die niet fout is en toch onbewijsbaar, ga wiskunde studeren en volg een cursus Mathematische Logica.

Nog weer later liet Cantor zien dat tussen een verzameling $X$ en de familie $\mathcal{P}(X)$ van alle deelverzamelingen van $X$ geen koppeling te maken is. Omdat $x \leftrightarrow \{x\}$ een koppeling maakt tussen $X$ en een deel van $\mathcal{P}(X)$ laat dit zien dat je bij elke soort oneindigheid weer een echt grotere soort kunt vinden. Het begrip ‘oneindig’ is dus veel rijker dan je zou denken.

Sommige wiskundigen uit de tijd van Cantor vonden dit wel vreemd allemaal en niet iedereen wilde de resultaten accepteren. Maar die mensen gingen uiteindelijk met pensioen en tegenwoordig moet iedere wiskunde wel wat Verzamelingenleer leren, en sommigen een heleboel.