Milli en Mu hebben de smaak aardig te pakken nu ze weten hoe ze allerlei spelletjes kunnen winnen. Ze spelen de laatste tijd alleen tegen vriendjes, want die weten nog niet hoe ze telkens de beste zet kunnen bepalen. Maar thuis is het wat stilletjes geworden omdat tegen elkaar spelen niet meer zo leuk is. Opeens krijgt Milli een idee en vraagt aan Phi of die misschien een spel kent dat nog niet is opgelost, want dan kunnen ze zelf weer samen op onderzoek gaan en plezier hebben.

Phi komt een dag later met het bordspel Hex thuis. Hex speel je met zijn tweeën op een ruitvormig bord van zeshoekige cellen. Een soort honingraat dus (zie figuur 1 voor een 7×7 bord). Elke speler heeft twee tegenoveroverliggende zijden van het bord toegewezen gekregen en beschikt over een eigen kleur stenen. Om de beurt plaatsen ze een eigen steen in een lege cel. De stenen die op het bord liggen mogen niet meer verplaatst worden. Het doel is om een aaneengesloten verbinding te maken tussen de eigen zijden. Degene die dat als eerste lukt, wint. Let op dat de hoeken voor beide spelers tellen.

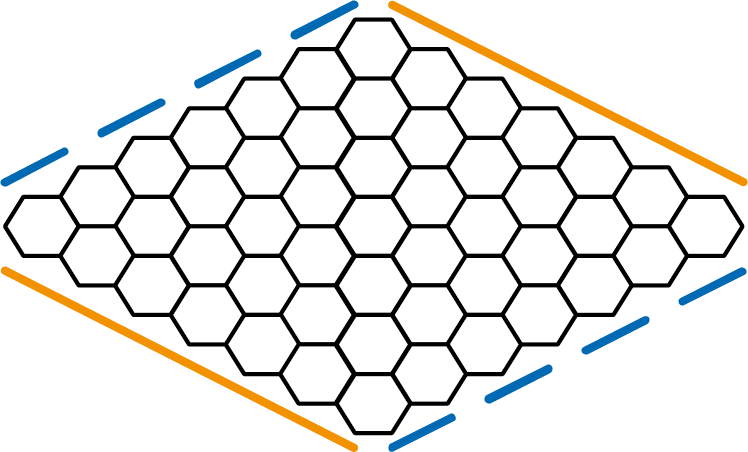
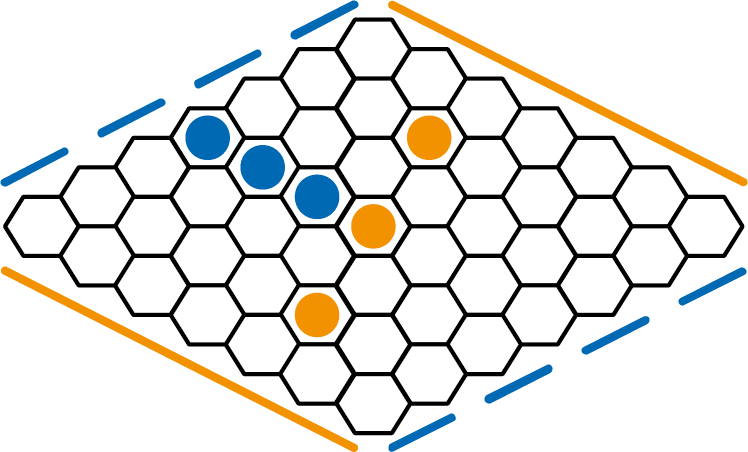
Mu is wel verbaasd dat een spel met zulke eenvoudige regels nog niet opgelost zou zijn. Hierover ontstaat ook wat onenigheid tussen Phi en Pi, want Pi beweert dat het spel wiskundig gezien wel degelijk is opgelost. Maar Phi houdt vol van niet. Tja, dat vonden Milli en Mu toch wat vreemd. Hun ouders waren het natuurlijk wel vaker oneens met elkaar. Maar over zoiets als het wel of niet opgelost zijn van een wiskundig probleem leek wat onwaarschijnlijk. Het werd nog gekker toen Phi en Pi zeiden dat ze het met elkaar eens waren. Het spel was opgelost en toch niet. Hoe is dat mogelijk? Hex bleek een schot in de roos. Een van de eerste dingen waar ze achter kwamen was dat het spel nooit in remise (gelijkspel) kan eindigen. Snap jij ook waarom dat zo is? Hex bleef een verrassend spel zonder dat duidelijk werd hoe je nou het beste kon spelen. Wel ontdekten Milli en Mu allerlei aardige trucjes. Bijvoorbeeld dat je een pad kan "schetsen" door twee lege cellen naast elkaar ertussen te laten. In de tweede figuur heeft Blauw met drie zetten een stevig pad gemaakt en Oranje heeft een pad geschetst. Maar als Blauw probeert het pad van Oranje te doorbreken, dan kan dat niet meer, omdat Oranje elke aanval kan afslaan. Kijk eens wat je zelf allemaal kunt ontdekken over Hex.

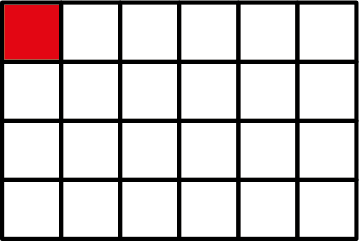
Pi kwam een paar dagen later met nog een onopgelost spel, waarvan Phi nu zei dat het echt wel was opgelost. Dat spel heet Chomp. Het begint met een rechthoekig blok chocolade opgebouwd uit vierkante blokjes (zie figuur 3 voor een 4×6 blok). Om de beurt moeten de spelers een blokje pakken samen met alle blokjes die er rechtsonder van liggen. Dat wil zeggen als je een blokje hebt gekozen (met × in figuur 4), dan zet je een mes in de linkerbovenhoek ervan en snijdt van daaruit een keer helemaal naar rechts en helemaal naar beneden (alle blauwe blokjes de figuur 4). Nou denk je misschien lekker al die chocolade. Maar dat valt tegen, want het blokje helemaal linksboven (rood in de figuur) is giftig en daar word je heel ziek van. Wie dat blokje pakt, die verliest. Het is dus maar beter om bescheiden te zijn.

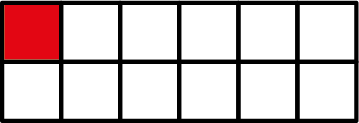
Ook hier konden Milli en Mu zich weer aardig mee vermaken. Je kunt Chomp ook eenvoudig op papier spelen, door bij elke beurt het zetnummer in alle gepakte blokjes te zetten. In figuur 5 en 6 zijn twee speciale blokken die na een aantal zetten kunnen ontstaan. Kun je ontdekken welke zet het beste is voor degene die aan de beurt is?

Net als bij Hex is er bij Chomp geen remise mogelijk. Bij zowel Hex als Chomp is natuurlijk de vraag hoe je kunt bepalen of degene die aan zet is kan winnen, en zo dat het geval is, met welke zet? Kijk eens of daar toch wat over te zeggen valt. Je kunt ook naar andere borden voor Hex kijken, zeg $N \times N$ en andere blokken voor Chomp, zeg $M \times N$.