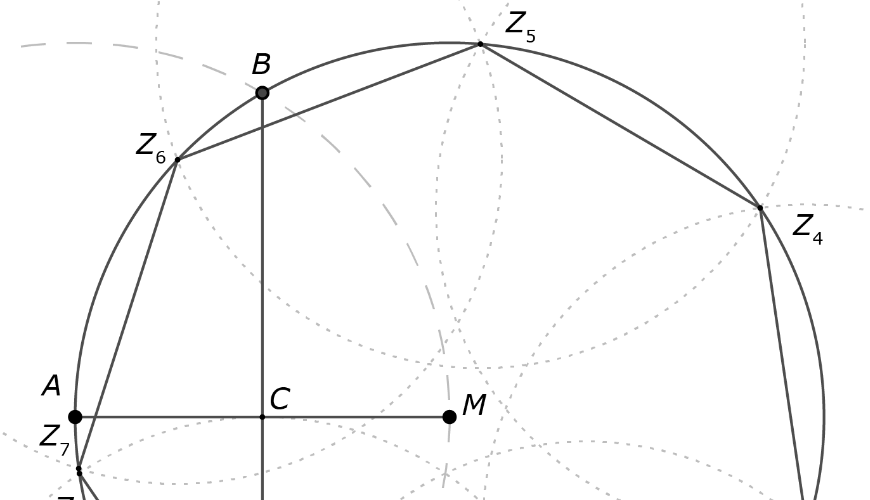
'Constructie' van een regelmatige zevenhoek
Constructies met passer en liniaal zijn een onderdeel van de meetkunde sinds de tijd van de oude Grieken. Een constructie met passer en liniaal is het wiskundig correct tekenen van een bepaalde figuur, lengte, hoek of punt met alleen een passer en liniaal. Hierbij bevat de liniaal geen schaalverdeling. Het construeren van een regelmatige veelhoek met louter passer en liniaal kan niet in alle gevallen.
Niet moeilijk zijn de gelijkzijdige 3-hoek, het vierkant en de gelijkzijdige 5-hoek. Als start is het de moeite waard om die nog eens te proberen.
Als je deze allemaal gevonden hebt, zijn de volgende ook niet moeilijk: de 6-, 8-, 10-, 12-, 16-, 20-, 24, 32-, 40, 48, 64-hoek. Om de 6-, 8- en 10-hoek te maken, hoef je alleen de middelpuntshoeken van de 3-, 4- en 5-hoek in tweeën te delen. Als je vervolgens alle middelpuntshoeken in vieren deelt, krijg je er nog veel meer. En een hoek in tweeën delen is gemakkelijk.
Maar welke n-hoeken kun je allemaal wel en welke niet met passer en liniaal maken?
Daarvoor bestaat een formule, die we hier geven, maar niet afleiden:
n = 2kp1p2 … ps
Hierin is k = 1, 2, 3, … en de pi zijn verschillende Fermatpriemgetallen. Een Fermatpriemgetal is een priemgetal van de vorm:
$$F_m = 2^{2^m}+1$$
De eerste vijf bekende Fermatpriemgetallen zijn: 3, 5, 17, 257, 65537 (m=0, 1, 2, 3, 4).
De wiskundige Carl Friedrich Gauss (1777-1855) bewees dat de eis aan n voldoende was om een regelmatige n-hoek met passer en liniaal te construeren. Hij bewees dat toen hij 19 jaar oud was! In 1836 bewees Pierre-Laurent Wantzel (1814-1848) dat deze voorwaarde ook noodzakelijk was.
‘Constructie’ van de 7-hoek
De eerste regelmatige veelhoek die niet met passer en liniaal te construeren is, is volgens de bovenstaande stelling dus de 7-hoek.
Maar in de hout- en metaalbewerking is het natuurlijk vaak gewenst om toch een regelmatige 7-hoek te maken. In Figuur 1 staat een extreem goede benaderingsconstructie gegeven.
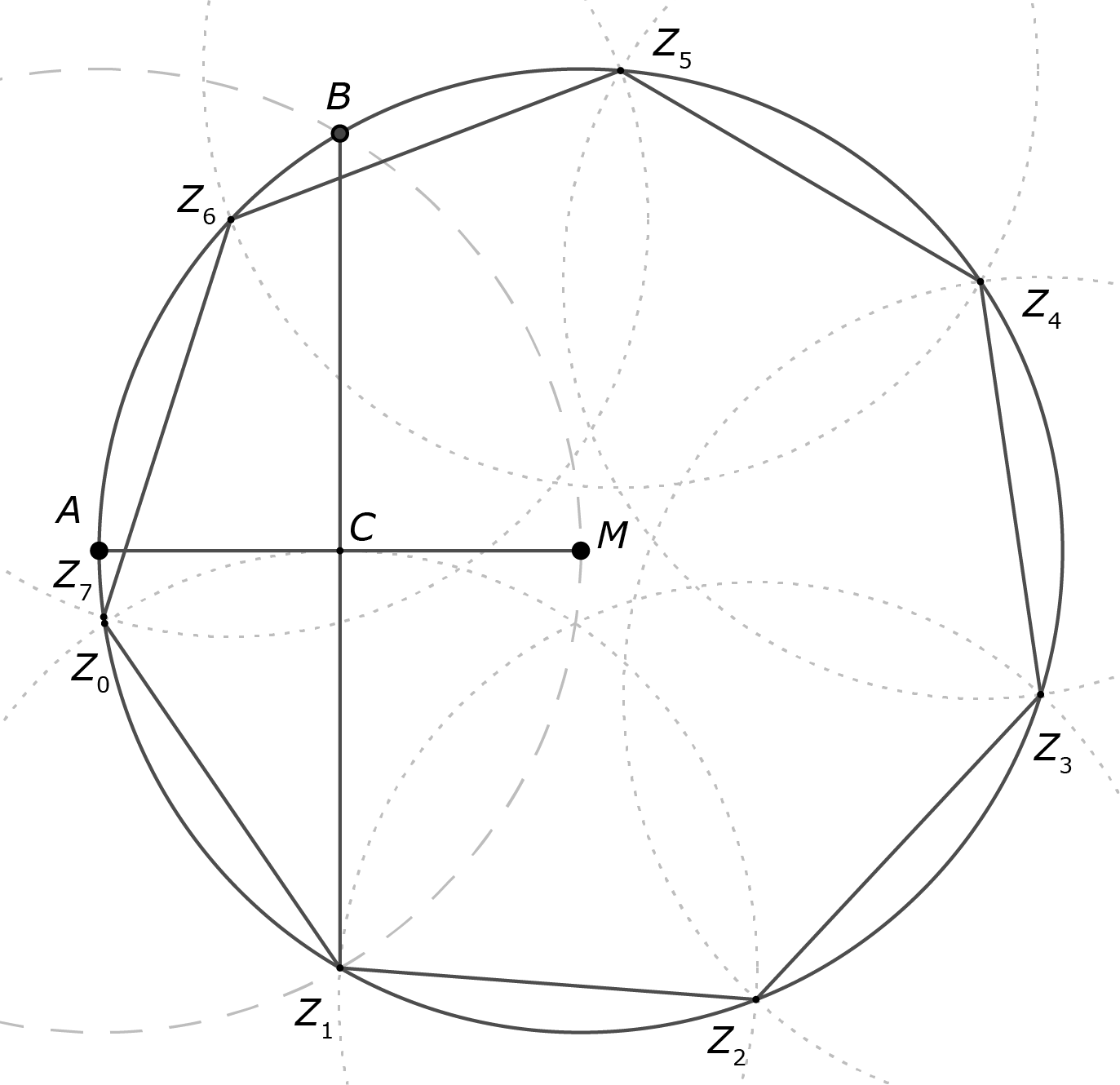
Start met een cirkel met straal 1 en middelpunt M. Neem een punt A op de omtrek en teken de cirkel met straal 1 en A als middelpunt. Noem de snijpunten met de eerste cirkel Z1 en B. Lijnstuk Z1B snijdt AM in C. De benaderde zijde van de regelmatige 7-hoek is dan Z1C. Herhaald omcirkelen levert dan de hoekpunten Z0, Z1, Z2, Z3, Z4, Z5, Z6 en Z7. In de tekening zie je al dat Z0 en Z7 net niet samenvallen. Zie voor een uitvergroting Figuur 2.
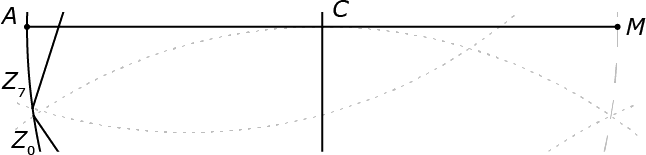
De fout in de constructie
Laten we een schatting maken van de fout die in deze constructie zit.
In Figuur 1 zie je dat voor de zijde z die deze constructie levert gelijk is aan:
$$z=\frac{1}{2}\sqrt{3} = 0,866025\dots$$
Vervolgens moeten we een schatting maken van de echte zijde van de regelmatige 7-hoek. Zie daarvoor Figuur 3.
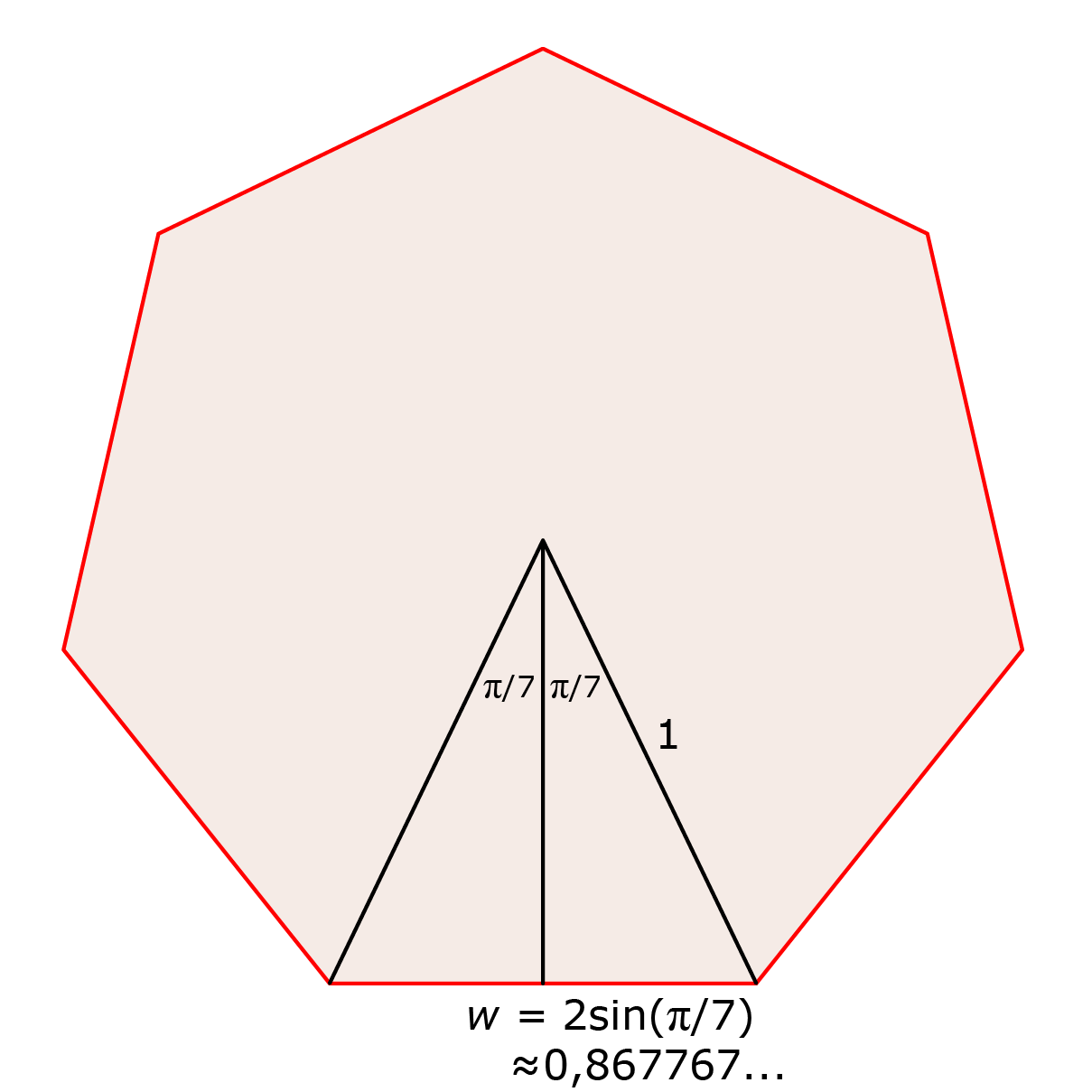
De middelpuntshoek is 2π/7. Voor de zijde w geldt dan:
$$w=2\sin\left(\frac{\pi}{7}\right)\approx 0,867767\dots $$
Voor de verhouding z/w hebben we dan:
$$\frac{z}{w}\approx 0,99799\dots$$
De fout in deze constructie is dus slechts 0,002. In een technische tekening dus verwaarloosbaar.
Bronnen
Op het internet is deze constructie terug te vinden. Ik hoorde van een kennis dat in de dertiger jaren van de vorige eeuw deze constructie al op de lagere technische scholen of ambachtsscholen in Nederland werd onderwezen.
Verder ontdekte ik dat de constructie ook stond in de derde aflevering van de Mathematical Pie van mei 1951. De Mathematical Pie was, net als Pythagoras, een wiskundetijdschrift voor jongeren, waarvan het eerste nummer verscheen in oktober 1950 in Engeland. Ruim tien jaar voor het eerste nummer van Pythagoras. De constructie werd toen naar het tijdschrift gezonden door J. Barkas, een leerling van Sidcot School in Somerset in Engeland.
Door wie en wanneer deze constructie voor het eerst bedacht is, is mij niet bekend.
