De oorspronkelijke Consul was een chimpansee die aan het begin van de 20e eeuw optrad in Britse theaters en zo beroemd werd dat hij in 1909 per boot, als passagier, de oversteek maakte naar Amerika met zijn kunstjes. Volgens de overlevering reed hij op de boot op zijn rode fiets en op rolschaatsen, gebruikte hij een zakdoek en een servet en at hij zijn lunch met mes en vork.

Eenmaal in Amerika bezocht hij de fabriek van het National Cash Register, waar hij leerde werken met een kassa. Een ingenieur die ook speelgoed ontwierp raakte hierdoor geïnspireerd en noemde het vermenigvuldigingsspeeltje dat hij zojuist had bedacht naar hem. Zo was Consul, the educated Monkey geboren.

Ook als je de tafels van vermenigvuldiging al lang kent, is Consul nog een interessant speelgoedje. Volgens de op het blik geprinte instructies moet je de voeten van de aap naar twee getallen laten wijzen, waarna Consul met zijn handen het product van die twee getallen zal tonen. Als je de voeten verschuift, verplaatsen de handen zich dankzij een mechanisch systeem met scharnierende punten bij de ellebogen, handen en kin. De grote vraag is hoe dit eigenlijk werkt. Als je niet echt aandachtig kijkt, zie je een driehoek met gehele getallen waarover zijn armen en handen bewegen. De driehoek van Pascal?

Beter kijken leert meteen dat het niet de driehoek van Pascal is. Die begint immers met

			$\color{red}{1}$
		$\color{red}{1}$		$\color{red}{1}$
	$\color{red}{1}$		$\color{red}{2}$		$\color{red}{1}$
$\color{red}{1}$		$\color{red}{3}$		$\color{red}{3}$		$\color{red}{1}$

terwijl Consuls driehoek begint met 

			$\color{red}{1}$
		$\color{red}{12}$		$\color{red}{4}$
	$\color{red}{11}$		$\color{red}{24}$		$\color{red}{9}$
$\color{red}{10}$		$\color{red}{22}$		$\color{red}{36}$		$\color{red}{16}$

Dat lijkt niet op elkaar. Het enige wat overeenkomt is de vorm, met de verspringende rijen gehele getallen.

StruCtuur in de getallenrijen zoeken

Om te begrijpen hoe de aap de getallen bij zijn tenen vermenigvuldigt, lijkt het een goed idee om uit te zoeken of er een structuur in de getallen op de diagonalen of de rijen in de driehoek van figuur 2 zit. Of wellicht allebei. De linker rand-diagonaal is makkelijk: op het bovenste cijfer na volgen de getallen van beneden naar boven een rij waarin ieder volgend getal het vorige plus één is, startend bij $2$. Van onderaf geteld staat op de $n$^e regel dus het getal $1 + n$. Op de volgende diagonaal nemen de getallen steeds met $2$ toe, beginnend bij $6$. De getallen vormen een zogenaamde rekenkundige rij. Op de ne regel staat dus het getal $4 + 2n$. Merk op dat ook deze formule geldt voor alle getallen behalve het bovenste.

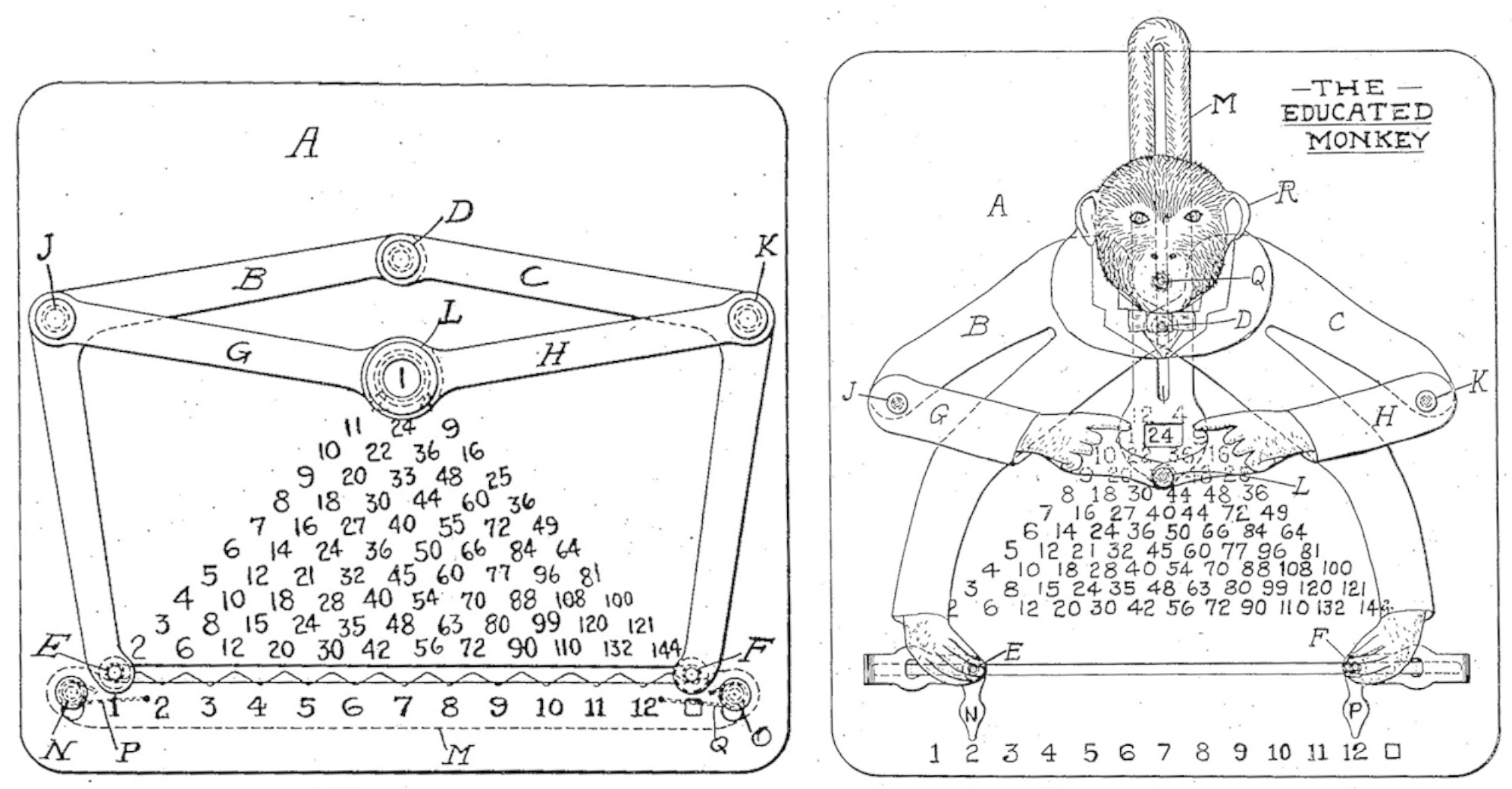
De patentdiagrammen van ingenieur William H. Robertson. Links het algemene vermenigvuldigapparaat (patent toegekend in 1918), rechts de speelgoedaap (patent verkregen in 1916).

 

Opgave 1 Zoek met behulp van figuur 2 uit wat het patroon is in de volgende diagonaal die vanaf het getal $12$ schuin naar rechtsboven loopt. Wat is de formule voor het element op de ne regel voor deze derde diagonaal, als $n = 1$ correspondeert met de onderste regel in de driehoek? Opgave 2 Probeer een algemene formule in termen van $n$ en $k$ te vinden voor de getallen op de $n$e regel in de $k$e diagonaal die van beneden schuin naar rechtsboven loopt.

De laatste getallen van deze diagonalen, waarvoor de gevonden formules niet gelden, vormen tezamen de rechterrand-diagonaal, waarin je waarschijnlijk kwadraten herkent. Van boven naar beneden zie je $1, 4, 9, 16, \ldots, 144$, ofwel $1^2, 2^2, 3^2, 4^2, \ldots, 12^2$. De andere diagonalen die vanaf de linkerrand schuin naar rechtsonder lopen, zijn ook heel simpel. Ze bevatten precies getallen van de tafels van vermenigvuldiging.

Relatie tussen beweging van handen en voeten

Zoals gezegd zijn de handen en voeten van de aap via bewegende punten met elkaar verbonden. Aan de hand van de patenttekening in figuur 2 is dit vrij duidelijk te zien. De handen zitten bij scharnierpunt $L$ in de oorspronkelijke tekeningen, de voeten bij eindpunten $E$ en $F$. Die eindpunten $E$ en $F$ schuiven in een horizontale sleuf van links naar rechts. En hoe dichter de voeten naar elkaar geschoven worden, des te lager de handen zitten en des te hoger de kop. Aan beide kanten vormen de benen en bovenarmen één stuk. Dat zie je duidelijk in de linker tekening in figuur 2, maar als je goed kijkt zie je dat het voor de aap in de rechter tekening ook geldt. Als de voeten een bepaalde afstand uit elkaar staan, zitten de handen altijd op dezelfde, door de voetafstand bepaalde, hoogte.

Kijk nu eens naar de handjes van de chimpansee. Waar komen deze te staan als je $1 \cdot 10$ uitrekent? En waar als je $2 \cdot 10$ aan de aap vraagt? Is het logisch dat de tafels van boven naar beneden lopen op deze diagonalen die schuin naar beneden gaan vanaf de linkerzijde?

We keren terug naar de diagonalen uit opgaven 1 en 2.

Als het goed is heb je voor de getallen op de $k$^e diagonaal de formule $k^2 + kn$ gevonden. Maar dat zijn natuurlijk veelvouden van $k$. Ofwel, de $k$^e diagonaal bevat getallen uit de tafel van $k$. Als zijn voetjes bij twee getallen staan, vindt de aap het product van die twee getallen dus precies op de kruising van twee diagonalen met de benodigde tafels. Om bijvoorbeeld $3 \cdot 6$ uit te rekenen, neemt hij de $3$^e diagonaal van linksonder naar rechtsboven, met getallen uit de tafel van $3$, en de diagonaal van linksboven naar rechtsonder die de tafel van $6$ bevat. Op de kruising vindt hij het getal $18$.

Het getal $18$ komt twee keer voor in de driehoek. Kunnen we begrijpen waarom de ene $18$ op de derde rij van onderen staat (dus op de rij met $n = 3$) en de andere op de zevende rij? Laten we daarvoor de horizontale rijen eens beter bekijken.

Met behulp van de zojuist gevonden formule $k^2 + kn$ zien we dat op de $3$^e rij van onderen in de ke diagonaal het getal $k^2 + k \cdot 3$ staat en op de $7$^e rij van onderen het getal $k^2 + k \cdot 7$. We zeiden al eerder, dat de handen altijd op een door de voetafstand bepaalde hoogte zitten. Omdat $k^2 + nk = k(k + n)$, kunnen we dit nu preciezer formuleren: als je twee getallen met elkaar vermenigvuldigt die $n$ verschillen, ligt het resultaat op de ne horizontale rij. Zie figuur 3.

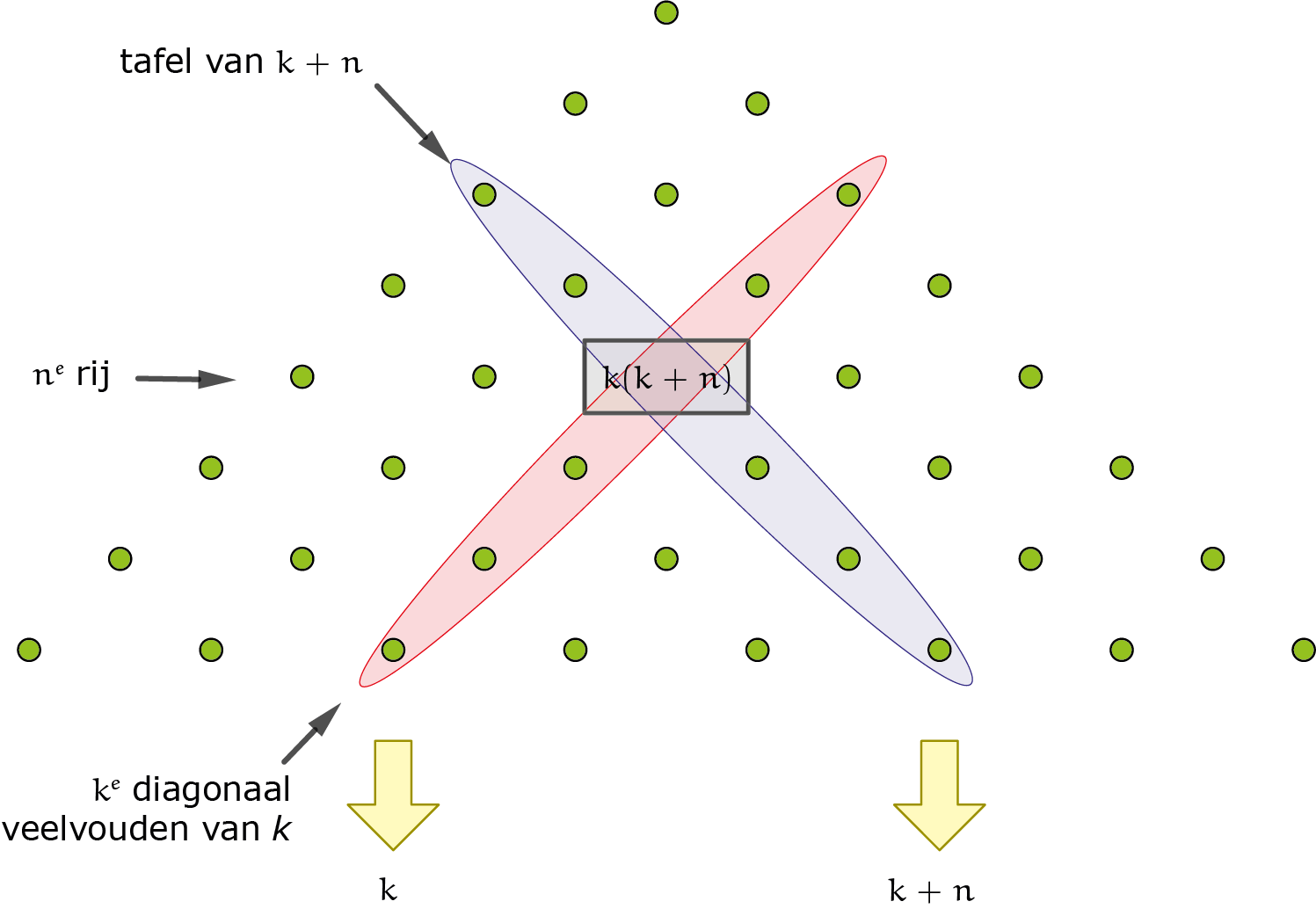
De getallen $3$ en $6$ verschillen een afstand $3$, dus ligt het getal $18 = 3 \cdot 6 = 3 \cdot (3 + 3)$ op de derde regel van onderen. Het getal $18 = 2 \cdot 9 = 2 \cdot (2 + 7)$ ligt op de zevende regel, omdat $2$ en $9$ een afstand $7$ uit elkaar liggen.

Opgave 3 Kijk naar de voetafstand voor ieder kwadraat en probeer daarmee te begrijpen waarom het getal behorend bij $k^2$ achteraan de $(13 - k)$e horizontale rij staat.

Kwadraten

De kwadraten zouden eigenlijk op de nulde rij moeten staan, dus een horizontale rij onderaan de driehoek. Immers, $k^2 = k(k + 0)$, zodat $n = 0$ in de bovenstaande analyse. De constructie van het blikken speelgoed, met voetjes die aan de achterkant in een smalle sleuf glijden, laat echter niet toe dat de voetjes op dezelfde positie staan. Daarom is er naast de $12$ nog een vierkant □ (square) geplaatst in de getallenrij onder de voeten. Als de rechtervoet daar staat en de linkervoet bij het getal $k$, geven de handen $k^2$ aan.

MeChaniCa en meetkunde

Nu we de rijenstructuur begrijpen kunnen we nog een vraag stellen over de werking van Consul: hoe zit hij eigenlijk in elkaar? Allereerst kun je zien dat er vier scharnierpunten zijn: op de ellebogen, net onder het vierkantje tussen de handjes, en net onder de kin. Op de ontwerptekening (figuur 2) zijn deze scharnierpunten aangegeven met de letters $J, K, L$ en $D$.

Het is niet moeilijk te begrijpen dat Consuls handjes over een horizontale lijn bewegen als de voeten op een constante afstand van elkaar gehouden worden, want in feite wordt de aap in zijn geheel naar links of naar rechts getransleerd als je hem bijvoorbeeld beweegt van $1 \cdot 4$ via $2 \cdot 5$, $3 \cdot 6$, et cetera naar $9 \cdot 12$. De scharnieren bij de handen, de ellebogen en het hoofd bewegen in dit geval niet.

De manier waarop de getallen in de driehoek zijn neergezet, suggereert dat de handen precies over een rechte lijn lopen als je één voet vasthoudt en de andere beweegt, dus als je bijvoorbeeld schuift van $4 \cdot 5$ via $4 \cdot 6$ en $4 \cdot 7$ naar $4 \cdot 8$. Dat dit ook echt zo is, kun je bewijzen met behulp van driehoeken. Bij Consul heeft driehoek $EJD$ een rechte hoek in $J$ en de lengtes $JD$ en $JE$ zijn gelijk. Hetzelfde geldt voor driehoek $FKD$. Daarmee zijn beide driehoeken gelijkbenig, en het is precies dit aspect dat belangrijk is. Een tweede belangrijke eigenschap van de aap is dat de onderarmen $JL$ en $KL$ ook weer dezelfde lengte hebben als $JD$, dus $JL = KL = JD = KD$. Daardoor vormen de punten $DJLK$ een ruit en liggen de handen $L$ en het hoofd $D$ op een verticale lijn. Voor de stevigheid heeft het speelgoed een verticale sleuf waar het hoofd in schuift, maar in feite legt de meetkunde deze verticale beweging gewoon vast.

In figuur 4 is de situatie schematisch weergegeven. Om te laten zien dat de handjes over een rechte lijn lopen als we de linkervoet vasthouden, moeten we aantonen dat $\angle LEF$ onafhankelijk is van de positie van de rechtervoet.

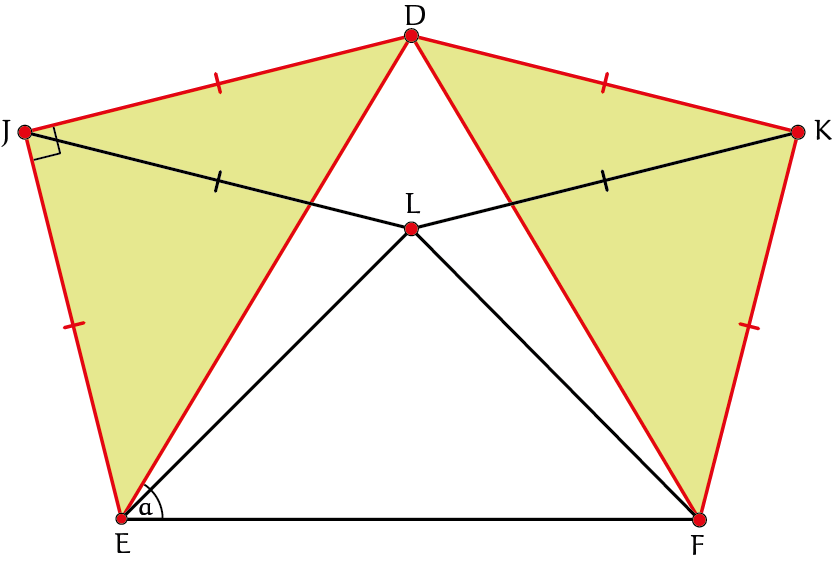
Laat $\angle DEF = \alpha$ , zoals in figuur 4. Als je de linkervoet vasthoudt en de rechtervoet verschuift, verandert de hoek $\alpha$. Vul op basis van wat je weet over driehoeken en ruiten de overige hoeken in de figuur in.

Opgave 4 Wat is de grootte van $\angle LEF$? Merk op dat deze waarde niet afhangt van $\alpha$.

Je antwoord op opgave 4 bevestigt dat de uitkomsten van vermenigvuldigingen van het getal $k$ met getallen $k + n$ precies op één rechte lijn moeten staan en dat die lijn een hoek van $45^{\rm o}$ met de lijn $EF$ maakt. Dit komt overeen met de manier waarop de getallen in de driehoek zijn gezet. En daarmee hebben we het functioneren van Consul de rekenaap ontrafeld.

Tot slot

De moderne, hernieuwde uitvoering van Consul kan alleen maar vermenigvuldigen, maar de oorspronkelijke uitvoering kwam met twee verschillende driehoeken die je onder de handjes kon stoppen. De tweede driehoek bevatte de getallen die je krijgt als je getallen $k$ en $k + n$ bij elkaar optelt. Je kunt zelf uitzoeken hoe die extra driehoek eruit moet zien.