Opdracht 1.

Is er een verdeling met drie zonen die wél precies 1 is? Dat betekent: zijn er gehele getallen $a, b$ en $c$ met $a < b < c$, waarvoor geldt dat $1/a + 1/b + 1/c$ gelijk is aan 1?

Antwoord. Het enig mogelijk drietal is $(a,b,c)= (2,3,6)$.

Stel $1/a + 1/b + 1/c = 1$, met $a < b < c$ en $a, b$ en $c$ geheel. 

Dan moet gelden $a \leq 3$, want $1/a + 1/b + 1/c \leq 1/a + 1/a + 1/a = 3/a$. De waarde van $a$ kan dus maximaal 3 zijn. Dus $a = 2$ of $a = 3$.

$a = 2$. Dan is $1/b + 1/c = 1/2$. Als $b \geq 4$ dan is $1/b + 1/c < 1/4 + 1/4 = 1/2$. Dat kan niet, dus $b = 3$ Dan volgt $c = 6$.

$a = 3$. Dan is $1/b + 1/c = 1 – 1/3 = 2/3$. Maar $b > 3$, dus is $1/b + 1/c < 1/3 + 1/3 = 2/3$. Dat kan niet. Dus $a \neq 3$.

Opdracht 2.

Bestaat er een verdeling op dezelfde manier als in vraag 1 onder vier zonen? Uit de parabel volgt direct het viertal (2, 3, 8, 18), maar zijn er nog meer oplossingen?

Antwoord. Er zijn, naast het genoemde (2,3,8,18) nog vijf andere viertallen mogelijk: (2,3,7,42), (2,3,8,24), (2,3,10,15), (2,4,5,20) en (2,4,6,12). Het laatste viertal maakt alleen gebruikt van even getallen.

Opdracht 3.

Is er ook een verdeling met vijf zonen?

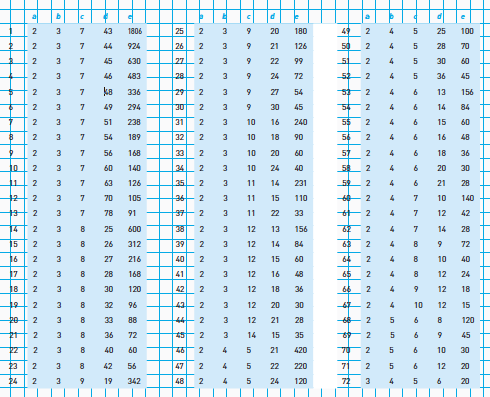
Antwoord. Voor vijf zonen zijn bijvoorbeeld mogelijk: (2,3,8,40,60), (2,3,9,30,45), (2,4,5,25,100) en (3,4,5,6,20). In de tabel hierboven staan alle 72 oplossingen voor vijf zonen. Daar zijn fraaie vijftallen bij. Een bijzondere oplossing is (2,3,7,43,1806). Afgezien van het feit dat de veestapel van de oude Arabier dan wel veel kamelen moet bevatten, maakt de verdeling dan gebruik van vier priemgetallen, die de ontbinding zijn van het vijfde getal, 1806 (= 2.3.7.43).

Oplossing (2,3,11,22,33) komt ons wegens $1/11 + 1/22 + 1/33 = 1/6$ bekend voor: $1/2 + 1/3 + 1/6 = 1$, de oplossing die we bij drie zonen ook al tegenkwamen. 

Zes oplossingen, waaronder (2,4,8,12,24), gebruiken alleen even getallen.

Nummer 67 (2,4,10,12,15) is de meest ‘compacte’ oplossing: zowel range (grootste minus kleinste getal: 13) als standaardafwijking (4,88) zijn de kleinst mogelijke.

Probeer zelf aan te tonen dat er geen oplossingen zijn met a > 4.