Honderden jaren geleden werden in verschillende steden over heel Europa astronomische klokken gemaakt, waar vaak allerlei berekeningen mee gemaakt konden worden, waaronder het bepalen van de dag van de week. In de figuren 1, 2 en 3 zie je bijvoorbeeld details van het 15e-eeuwse Horologium mirabile Lundense, te vinden in de kathedraal van de zuid-Zweedse stad Lund. Maar ook zonder retour-ticket naar de dichtstbijzijnde stad met zo’n klok was het al een hele tijd mogelijk om de dag van de week uit het hoofd uit te rekenen bij een bepaalde datum. We bekijken de formule van Carl Friedrich Gauss en de doomsday-rule van John Conway (die juist rond het verschijnen van dit nummer van Pythagoras overleden is) maar keren eerst nog kort even terug naar de klok in Lund.

De klok in Lund

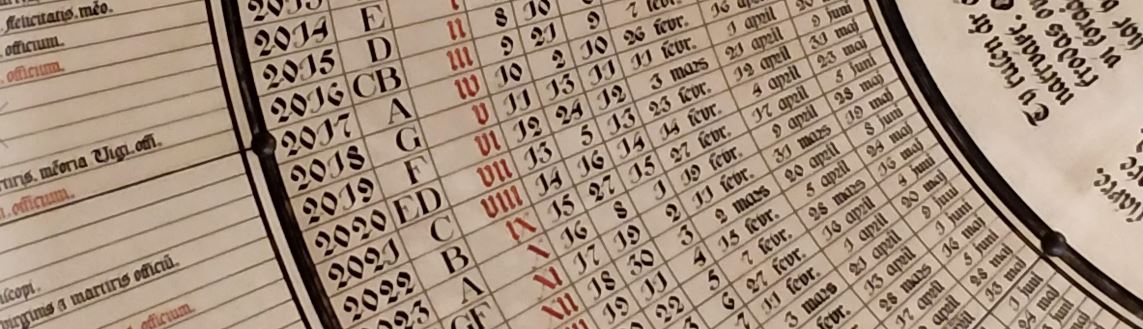
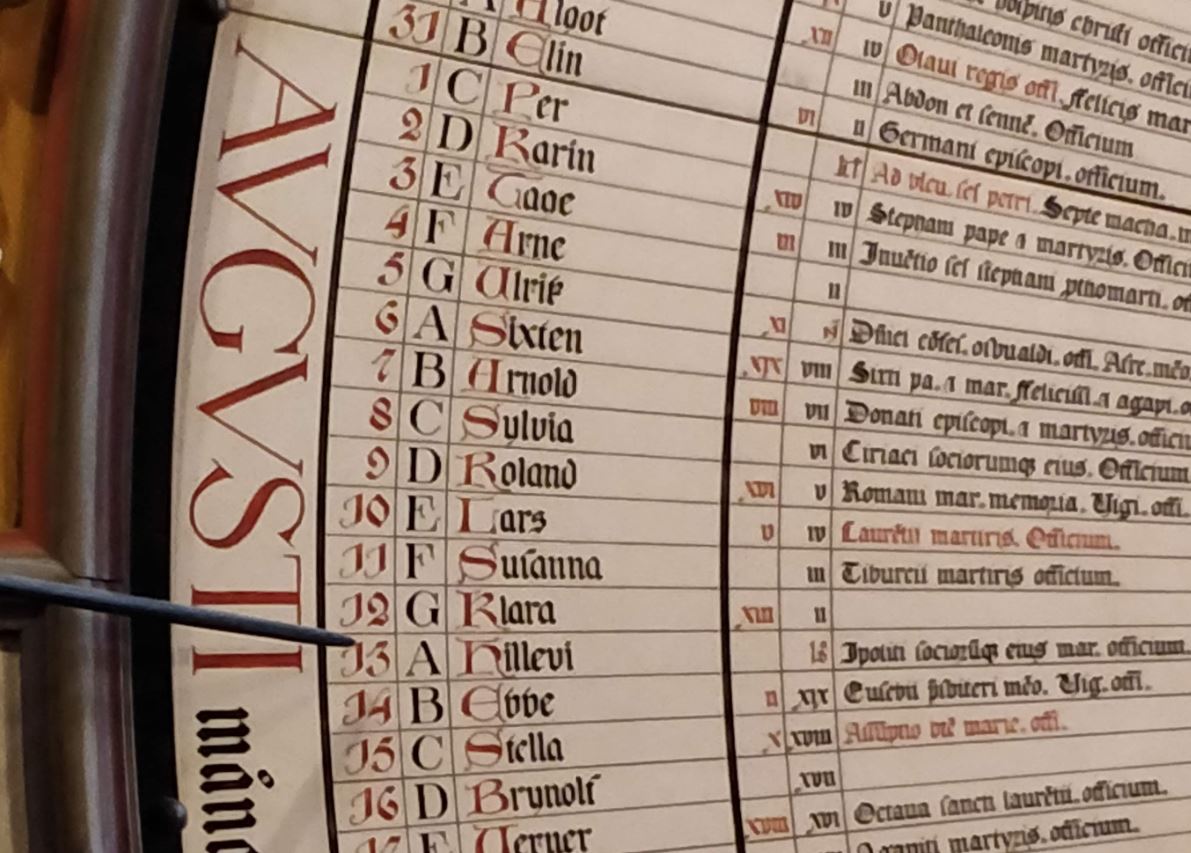
In figuur 1 zie je de legenda van het midden van de klok waar informatie per jaartal gegeven wordt. Voor ons van belang is de buitenste ring met het jaartal zelf, en de ring ernaast met de Littera Dominicalis, de zogenaamde zondagsletter. Deze letter duidt aan welke dagen van het jaar op een zondag vallen, waarbij 1 januari overeenkomt met de letter $A$, 2 januari met $B$, ..., 7 januari met $G$, 8 januari terug met $A$, enzovoort. (Let op: 29 februari krijgt géén letter, aangezien deze niet in elk jaar voorkomt.) In figuur 2 kan je aflezen dat 2019 een $F$-jaar is, waardoor we dus alvast weten dat de eerste zondag op 6 januari viel. Voor een schrikkeljaar heb je twee letters nodig door het toevoegen van een extra dag in februari: de eerste letter duidt op de zondagen voor 29 februari, de tweede letter op de zondagen vanaf 1 maart. 2020 is volgens de klok een $ED$-jaar, en inderdaad, de eerste zondag is op 5 januari, maar vanaf maart zijn het de $D$-dagen die op zondag vallen, te beginnen met 1 maart. Figuur 3 geeft dan weer een detail van de informatie aan de buitenkant van de klok waar er per dag van het jaar van alles staat opgesomd, waarbij wij kijken naar de dag van de maand in de buitenste ring, en de corresponderende letter (waarvan eerder al sprake) in de ring ernaast. Met behulp van die letter, in het geval van 13 augustus (de dag van mijn bezoek aan Lund) is dit de $A$, kunnen we dus de dag van de week bepalen, in combinatie met de zondagsletter van het jaar, de letter $F$ in het geval van 2019. We weten al van de gouden letter dat deze in dat geval de zondagen aanduidt, met andere woorden: alle $F$-dagen vallen op zondag in een $F$-jaar. In figuur 3 kan je dan ook zien dat 11 augustus een zondag was. Bijgevolg was 12 augustus ($G$) een maandag, en 13 augustus ($A$) een dinsdag. Het volstaat dus om door te tellen vanaf de dichtstbijzijnde zondag, maar in onderstaande samenvattende tabel kan je dit ook gemakkelijk aflezen: bovenaan staan de zondagsletters van het jaartal, links de letter van de datum waarvan je de dag wilt weten.

$A$

$B$

$C$

$D$

$E$

$F$

$G$

$A$

zo

za

vr

do

wo

di

ma

$B$

ma

zo

za

vr

do

wo

di

$C$

di

ma

zo

za

vr

do

wo

$D$

wo

di

ma

zo

za

vr

do

$E$

do

wo

di

ma

zo

za

vr

$F$

vr

do

wo

di

ma

zo

za

$G$

za

vr

do

wo

di

ma

zo

Nogmaals met hetzelfde voorbeeldje als hierboven: 2019 is een $F$-jaar, dus we kijken in de kolom onder $F$. Aangezien 13 augustus een $A$-dag is, lezen we op de $A$-lijn af dat dit een dinsdag was. Ook voor schrikkeljaren kunnen we dit doen en gebruik maken van deze tabel, al moeten we dan een beetje opletten. Zoals eerder reeds gezegd, bestaat de zondagsletter van een schrikkeljaar uit 2 letters, eentje die dient om te rekenen vóór 29 februari, en eentje om te rekenen erna. 2020 is bijvoorbeeld een $ED$-jaar volgens de klok. We bekijken even hoe dit dan in z’n werk gaat:

• 1 januari is per definitie een $A$-dag. Omdat 1 januari voor 29 februari valt, gebruiken we de eerste letter van de zondagsletter, zijnde de $E$. Deze combinatie levert ons in bovenstaande tabel woensdag op, wat wil zeggen dat 1 januari 2020 op een woensdag valt.
• 1 mei daarentegen is een $B$-dag (dat staat op de klok, al is dat niet zichtbaar op deze foto’s), en valt uiteraard na 29 februari. We zoeken dus in de kolom van de tweede zondagsletter, zijnde de $D$, op de $B$-rij, en vinden dat 1 mei 2020 een vrijdag moet zijn.
• We haalden reeds aan dat 29 februari geen eigen letter krijgt (al is dat niet te zien op de foto’s). Je kan uiteraard wel bovenstaande methode gebruiken om de dag van de week voor 28 februari ($C$) uit te rekenen in een schrikkeljaar aan de hand van de eerste zondagsletter, en daaruit die van 29 februari afleiden. Of je rekent die voor 1 maart ($D$) uit met behulp van de tweede zondagsletter, en leidt dan daar weer die van de dag ervoor af. Aan u de keuze, maar beide geven uiteraard hetzelfde resultaat.

De formule van GausS

Uiteraard is bovenstaande methode met behulp van een gigantische klok en een tabel niet heel efficiënt. Knappe wiskundige koppen hebben in de loop van de geschiedenis dan ook verschillende algoritmes ontwikkeld om de dag van de week te bepalen bij een gegeven datum. De meeste van deze algoritmes maken ook nog gebruik van een of andere tabel om getallen in op te zoeken, afhankelijk van het jaar of de datum die je zoekt. Maar er bestaan er ook volledig onafhankelijk van enig opzoekingswerk, die je dus (in principe) volledig uit het hoofd kan doen, zo ook de formule van Gauss. Deze gaat als volgt:

$$w = R\left(6 + D + \lceil M \times 2{,}6 \rceil + 5 \times R(Y;4)+4\times R(Y;100)+6\times R(Y;400);7\right)$$

waarbij

• $D$ de dag van de datum is die je wil uitrekenen ($1$ tot $31$);
• $M$ de maand is. Maar let op: we tellen hierbij zoals de Romeinen vanaf maart (dus maart = $1$, april = $2$, …, december = $10$, januari = $11$, februari = $12$);
• $Y$ het jaar is, maar voor datums in januari of februari doe je dit nog min $1$; 
• $\lceil \cdot \rceil$ afronden naar boven is;
• $R(a ; b)$ de rest bij deling is van $a$ door $b$. 

Het resultaat $w$ is dan een cijfer van $0$ tot $6$, wat staat voor de dagen van de week ($0$ is zondag, $1$ is maandag, …, $6$ is zaterdag). We proberen het te verduidelijken met een voorbeeldje, zijnde dezelfde datum als hierboven, 13 augustus 2019:

1. Met de definities van hierboven (denk eraan: $M$ is het Romeinse maandgetal!): $D = 13$, $M = 6$ en $Y = 2019$.
2. Hieruit volgt dat $R(Y ; 4) = 3$, want $2019 : 4 = 504$ met rest $3$. Analoog geldt dus ook dat $R(Y ; 100) = 19$ en $R(Y ; 400) = 19$.
3. $M \times 2{,}6 = 15{,}6$ wat na afronden naar boven $16$ wordt.
4. De formule wordt dan $w = R(6 + 13 + 16 + 5 \times 3+4\times 19+6\times 19;7)$ wat na een beetje rekenwerk uitkomt op w $= R(240 ; 7) = 2$. 13 augustus 2019 was dus een dinsdag, zoals de kalender in Lund ook reeds aangaf.

Of nog een tweede voorbeeldje met de sterftedatum van Gauss, zijnde 23 februari 1855:

1. $D = 23$, $M = 12$, $Y = 1854$ (want we moeten $1$ van het jaartal aftrekken aangezien we een datum in februari willen uitrekenen.
2. Hieruit volgt $R(Y ; 4) = 2$, $R(Y ; 100) = 54$ en $R(Y ; 400) = 254$.
3. $\lceil 2{,}6\times 12\rceil = \lceil 31{,}2\rceil = 32$.
4. De totale formule: $R(6 + 23 + 32 + 5 \times 2 + 4 \times 54 + 6 \times 254 ; 7) = R(1811 ; 7) = 5$. Gauss stierf dus op een vrijdag.

De doomsday-rule

Toegegeven, om deze formule van buiten te leren, laat staan dit helemaal uit het hoofd uit te rekenen, moet je toch al een klein rekenwonder zijn. Er zijn echter nog andere trucs om data uit het hoofd te bepalen. De bekendste is misschien wel de zogenaamde doomsday rule, in 1973 ontwikkeld door de Britse wiskundige John Conway, vooral bekend van zijn Game of Life. Hij merkte op dat in eender welk jaar er bepaalde makkelijk te onthouden datums zijn die telkens op dezelfde dag vallen: 4-4, 6-6, 8-8, 10-10, 12-12 en de laatste dag van februari, maar ook 9-5 en 5-9 (te onthouden door een nine-to-five job) alsook 11-7 en 7-11 (bekend van een niet nader genoemde Japans-Amerikaanse winkelketen). Deze dag wordt dan de doomsday van het desbetreffende jaar genoemd. Voor 2019 was dit donderdag, voor 2020 is het zaterdag. Vanaf de datum in kwestie kan je dus makkelijk vooruit of achteruit tellen naar de dichtsbijzijnde doomsday, om zo de dag van de week te berekenen. Tenminste, als je de doomsday van dat jaar kent. Ook daar zijn echter simpele algoritmes voor ontwikkeld, bijvoorbeeld:

$$\mbox{doomsday } = R\left(y + \left\lfloor\frac{y}{4}\right\rfloor ; 7\right)+\mbox{ anchorday}$$

waarbij

• $y$ de laatste twee cijfers zijn van het jaartal;
• $\lfloor \cdot \rfloor$ afronden naar beneden is;
• $R(a ; b)$ opnieuw de rest is bij deling van $a$ door $b$; 
• $\mbox{anchorday}$, oftewel de anker-dag van het jaartal, specifiek is voor elke periode van 100 jaar. Later meer hierover.

Opnieuw een voorbeeldje om deze berekening te verduidelijken, nog steeds met 13 augustus 2019:

1. In ons geval is $y$ gelijk aan $19$.
2. Deel dat cijfer door $4$, en rond af naar beneden. We krijgen dan in ons voorbeeld $4$.
3. Tel dit op bij het oorspronkelijke (twee-cijferige) jaartal. De som van $4$ en $19$ is $23$.
4. Neem de rest van deze som bij deling door $7$. De rest van $23$ gedeeld door $7$ is $2$.
5. Tel dit getal op bij de anker-dag van de eeuw waarin je datum zich bevindt. De anker-dag voor 2000-2099 is dinsdag. twee dagen verder is dus donderdag, wat de doomsday is voor 2019.
6. We weten dat in augustus de achtste van de maand (8-8) op de doomsday, donderdag dus, valt. 13 augustus is $5 $ dagen later, en is bijgevolg een dinsdag, wat we uiteraard al wisten.

Het enige wat we dus nog moeten weten is de zogenaamde anker-dag van een eeuw (al is eeuw hier met een korrel zout te nemen, want voor deze berekeningen gaan eeuwen van ..00 tot ..99, wat niet overeenkomt met de traditionele definitie van een eeuw). Vermits de Gregoriaanse kalender zichzelf om de $400$ jaar herhaalt, zullen ook de anker-dagen zich om de $400$ jaar herhalen. Voor 2000-2099 zagen we al dat deze anker-dag een dinsdag is, en bijgevolg zal dat ook in de 16..-jaren geweest zijn. Dit tabelletje is dus voldoende om uit het hoofd te leren, om daarmee de doomsday van eender welk jaar uit te rekenen, en bijgevolg de weekdag van eender welke datum te kunnen bekomen:

“Eeuw”		Ankerdag
1800-1899		vrijdag
1900-1999		woensdag
2000-2099		dinsdag
2100-2199		zondag

Tot slot

Mits wat oefening kunnen de twee algoritmes hierboven zeker en vast tot wat leiden. John Conway, de uitvinder van het doomsday- algoritme, kan meestal in minder dan 2 seconden het correcte antwoord bij een willekeurige datum geven. Er bestaat zelfs een tweejaarlijks wereldkampioenschap hoofdrekenen, waarbij een van de disciplines is om in een minuut zo veel mogelijk juiste weekdagen bij willekeurige datums (tussen 1600 en 2100) te plaatsen. Andere disciplines zijn onder andere het vermenigvuldigen van twee getallen met 8 cijfers of de vierkantswortel berekenen van getallen met 6 cijfers. Belgen deden nog nooit mee aan de eindronde. Nederlanders hebben wel al enkele mooie resultaten behaald met onder andere Jan van Koningsveld (die tegenwoordig voor Duitsland uitkomt) en Willem Bouman. Over de hoofdrekencapaciteiten van Willem Bouman lees je in een volgende Pythagoras meer. IJs, weder en corona dienende vindt het volgende kampioenschap plaats van 21 tot 23 augustus 2020 in de Duitse stad Paderborn. Het wereldrecord kalenderrekenen? Dat staat op naam van de Amerikaan Yusnier Viera Romera, die in januari 2018 maar liefst 140(!) correcte antwoorden gaf, nog steeds binnen die ene minuut. Oefening baart kunst, zegt men dan.