In de vorige jaargang van Pythagoras is in verband met de prijsvraag veel aandacht besteed aan vlakvullingen. Een vlakvulling of betegeling is een opvulling van een oppervlak veelal door veelhoeken die allemaal dezelfde vorm en grootte hebben zonder overlap of openingen. Meestal gaat men er stilzwijgend van uit dat de stempels of tegels een plat vlak moeten bedekken. Maar dat hoeft niet. Je kunt ook zeggen: een betegeling is een patroon gemaakt van identieke vormen (tegels) die zonder gaten of overlap in elkaar passen. Met bijvoorbeeld identieke L-vormige tegels kun je een betegeling maken zoals in figuur 1. De tegels vullen keurig een plat vlak op. Maar het kan ook anders zoals in figuur 2. Daar zie je met dezelfde L-vormige tegels een niet-vlakke betegeling zonder overlap of gaten. Dat geldt ook wanneer we de tegels combineren zoals in figuur 3. Het resultaat is een cilindrische betegeling. Hier eveneens geen overlap of gaten.

Ruimtelijke betegeling

Vierkante tegels zijn de meest voor de hand liggende vormen om platte vlakken op te vullen. Maar je kunt er ook een niet-vlakke betegeling mee maken zoals in figuur 4. Ook hier weer een structuur zonder overlap of gaten. De meest eenvoudige manier om met vierkanten een ruimtelijke betegeling te maken is door ze te combineren tot een kubus (figuur 5). Doorgaans zijn we echter niet geneigd dit als een betegeling op te vatten.
Net als de kubus kunnen ook de andere regelmatige veelvlakken worden opgevat als ruimtelijke betegelingen (figuur 6). Merk daarbij op dat een regelmatige vijfhoek gebruikt kan worden voor een ruimtelijke betegeling (het regelmatig twaalfvlak)
maar niet voor een vlakke betegeling!

Elevatie: verhoogde veelvlakken

Het zogenaamde elevatieproces dat Leonardo da Vinci toepaste op regelmatige veelvlakken levert achteraf beschouwd een opmerkelijke uitbreiding in de richting van ruimtelijke betegelingen. Het komt erop neer dat hij bijvoorbeeld op alle vier zijvlakken van een regelmatig viervlak eenzelfde regelmatige viervlak zette (figuur 7). In het algemeen kan dit elevatieproces van een veelvlak als volgt worden beschreven. Neem het middelpunt van een zijvlak van het veelvlak. Til het dan bij wijze van spreken loodrecht op het vlak omhoog totdat de afstand van dit punt tot elk van de hoekpunten van dit betreffende zijvlak gelijk is aan de lengte van een zijde van dat regelmatig zijvlak. Doe dit voor elk zijvlak van het regelmatig veelvlak.
Zo zie je in figuur 8 nog twee tekeningen van Leonardo da Vinci met een verhoogd regelmatig twaalfvlak of verhoogde dodecaëder (figuur 8a) en een verhoogd regelmatig twintigvlak of verhoogde icosaëder (figuur 8b). Omdat de nieuwe  zijvlakken allemaal gelijkzijdige driehoeken worden, is het duidelijk dat dit proces alleen maar werkt op driehoekige, vierkante en vijfhoekige zijvlakken.

Draaiing

Op één na, te weten het regelmatig twaalfvlak, hebben we voorbeelden van ruimtelijke en niet-vlakke betegelingen gezien waarvan de tegels ook gebruikt kunnen worden voor vlakke betegelingen. Zou het mogelijk zijn om andere vormen van 
tegels te vinden die alleen kunnen worden gebruikt voor niet-vlakke of ruimtelijke betegelingen? Voor het antwoord bekijken we nogmaals de tekening met de verhoogde icosaëder van Leonardo da Vinci (figuur 8b). Deze kan worden gezien als
een samenstel van twintig driehoekige piramides met in totaal zestig (twintig keer drie) zijvlakken. Nu veranderen we de vorm van de tegels door elke piramide over eenzelfde hoek om zijn eigen as te draaien. We krijgen dan een nieuw objecten
zoals in de figuren 9 en 10. In elke fase of tussenstand van de draaiing is de vorm van elk van de zestig tegels veranderd van een gelijkzijdige driehoek in een niet-convexe vijfhoek. En in elke fase is de vorm van de tegels hetzelfde. Het object in figuur 10 kan worden herkend als een vervlechting van vijf tetraëders, maar hier is het gewoon een verzameling van zestig gelijkvormige tegels die een niet-vlakke betegeling vormen.

SpiraalCilinders

De beschreven methoden van elevatie en draaiing en combinaties daarvan leveren veel inzicht in ruimtelijke betegelingen. Ze zijn echter ontoereikend om te komen tot de kunstwerken van Rinus Roelofs langs de Doorbraak. Daar heeft hij een andere aanpak voor ontwikkeld waarmee nieuwe vormen van tegels voor cilindrische betegelingen worden verkregen.

Eerst wordt een normale spiraalcurve getekend. Deze wordt onderverdeeld in gelijke stukken. Daarna wordt een rechte lijn getrokken van het startpunt aan de onderkant van spiraal naar het startpunt van het volgende stuk, enzovoorts. Deze rechte lijnen worden vervolgens naar beneden samengedrukt (geëxtrudeerd) naar de as van de spiraal (figuur 11). Een tweede spiraalachtige vorm zoals in figuur 11 wordt ondersteboven gedraaid en toegevoegd aan de oorspronkelijke (figuur 12) waarbij de assen samenvallen. Deze spiraalvormen kruisen elkaar en van de snijlijnen is de uiteindelijke vorm van de tegels af te leiden. De vorm van de voltooide tegel is in het afgebeelde voorbeeld een niet-convexe zeshoek (figuur 13). Deze kan niet worden gebruikt om een plat vlak te betegelen.

Variaties

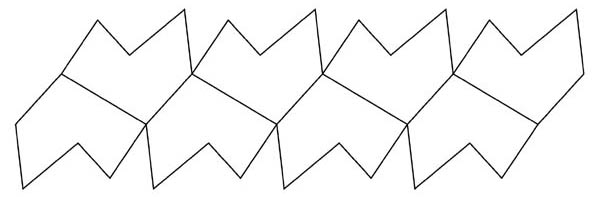
Uitgaande van eenzelfde spiraal laat deze methode veel variaties toe zoals de afstand tussen de punten op de spiraal, de hoek waaronder de extrusie plaats vindt en de positie van de tweede spiraalvorm waarbij zowel de hoogte als de rotatiehoek kan variëren. Elke reeks waarden levert een andere tegelvorm. De spiraalvormige cilinder in figuur 14a kan zelfs worden uitgerold tot een eenvoudige strook tegels die vervolgens als een soort bouwplaat weer in elkaar kan worden gerold. Te vergelijken met de uitslag van een regelmatig veelvlak. Als voorbeeld kun je figuur 14b afrollen tot 14c.

De praktijk

Het tekenen en verder bewerken van de spiraal waarmee wordt begonnen, wordt met hulp van aparte software op de computer gedaan. Daarmee kunnen snel allerlei variaties worden uitgevoerd om te komen tot aantrekkelijke resultaten zoals de figuren 13 en 14. De zeven beelden langs de Doorbraak vormen dan ook een selectie uit de grote hoeveelheid mogelijkheden. Met dezelfde software kan het gekozen resultaat
ook worden uitgerold. Dat levert dan stroken zoals in figuur 14c. Die kunnen op stevig papier worden uitgeprint en uitgesneden. Daarna kan met zo’n strook een papieren model van de betreffende cilindrische spiraal in elkaar worden gedraaid. Zo’n strook is dus in feite niets anders dan een bouwplaat waarmee een papieren model kan worden gemaakt. 

Het papieren model kan vervolgens dienen als voorbeeld en als uitgangspunt voor de schaalvergroting die moet plaatsvinden. Voor elk beeld moet een serie grote ijzeren tegels worden uitgesneden die vervolgens aan elkaar gelast worden. Het eindresultaat zie je hieronder.

	Op de website www.rinusroelofs.nl kun je meer foto’s zien over het maakproces van de kunstwerken en animaties over nietvlakke betegelingen. Tot eind november zijn op het Stationsplein van Hengelo acht andere grote beelden van Rinus Roelofs te bewonderen.

 

Wil je zelf een papieren model van een van de kunstwerken van De Doorbraak maken? Stuur een mailtje naar Klaas Lakeman van Ars et Mathesis [email protected] en bestel voor een kleine bijdrage in de kosten een bouwplaat zoals in figuur 14c.