De getallen van Catalan
De getallen $B(n)$ zijn nauw verwant met de Catalan-getallen. Het $n$-de Catalan-getal is als volgt gedefinieerd:
$$C(n)= \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{n!(n+1)!}$$
voor $n ≥ 1$. Per definitie is $C(0) = 1$.
De rij Catalan-getallen begint dus zo:
$$1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ...$$
In de OEIS vind je deze rij onder nummer A000108. Hier staan vijf toepassingen van de Catalan-getallen.
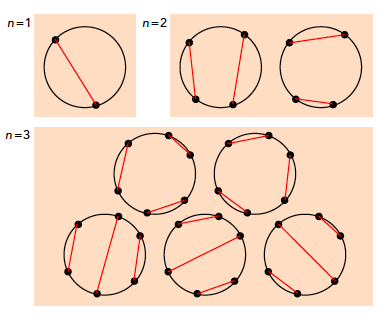
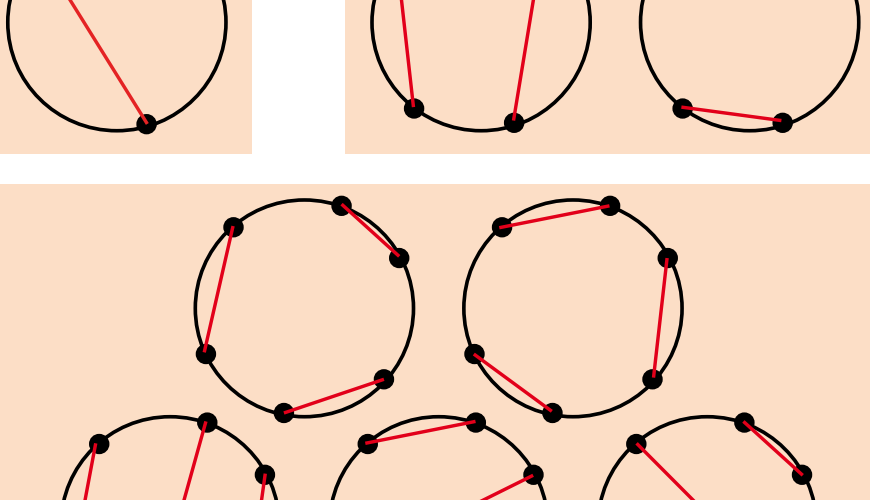
ronde tafel simultaan elkaar de hand kunnen schudden
(eventueel over de tafel heen) zonder kruisingen.

van de vorm $a_1 a_2 ... a_n$ met alle $a_i$’s minstens gelijk
aan $1, a_1 ≤ a_2 ≤ ... ≤ a_n$ en $a_i ≤ i$.

(zoals sinaasappels) als je onderaan begint met een rij met n munten.
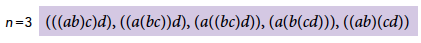
plaatsen in een product met n + 1 factoren.
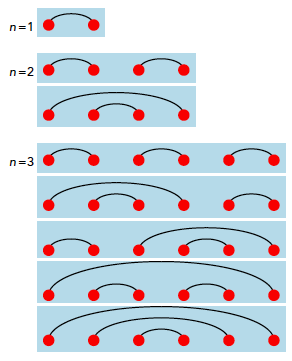
lijn twee per twee te verbinden met boogjes die elkaar
niet snijden (waarbij de boogjes boven de punten liggen).
