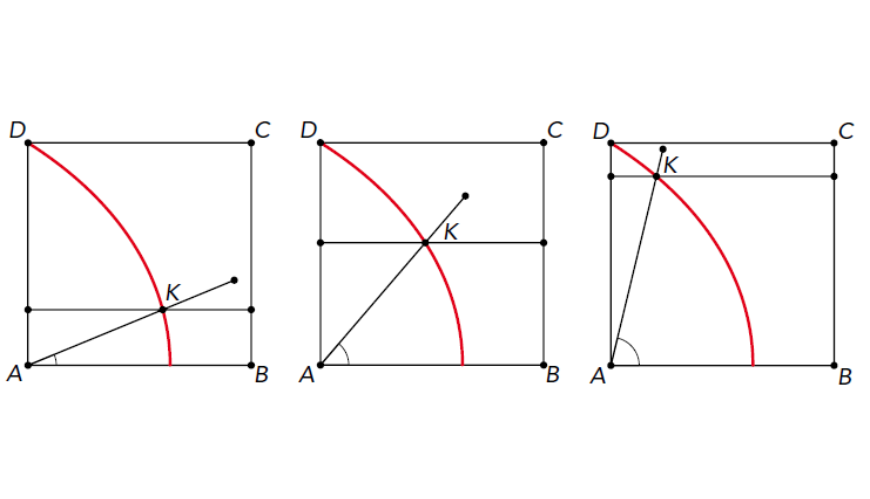
De kwadratrix is een bijzondere kromme. De eenvoudigste manier om hem te beschrijven gaat via beweging. Stel je voor: je hebt een vierkant $ABCD$ met zijde $1$ (of een andere zijde, dan gaat het verhaal verder niet essentieel anders).

Nu laat je een lijn die begint op lijn $AB$ om hoekpunt $A$ draaien met een constante snelheid, en wel zó dat na $1$ tijdseenheid de lijn op $AD$ terechtkomt. Tegelijkertijd laat je een lijn die begint op $AB$ met constante snelheid omhoog bewegen, op zo’n manier dat die lijn na $1$ tijdseenheid samenvalt met lijn $DC$. Op elk moment snijden de draaiende en de omhoog bewegende lijn elkaar in een punt $K$. De kwadratrix bestaat nu uit alle punten $K$ die je op die manier krijgt. Hoe ziet dat er op verschillende momenten in het proces uit? Figuur 1 laat het zien voor achtereenvolgens $t = 0{,}25$, $t = 0{,}55$ en $t = 0{,}85$. De rode lijn geeft de resulterende kromme weer.

Formule

Om een formule voor de punten op de kwadratrix te maken, is het handig om in coördinaten te denken. We leggen de oorsprong op punt $A$, de $x$-as langs $AB$ en de $y$-as langs $AD$ (zie figuur 2).

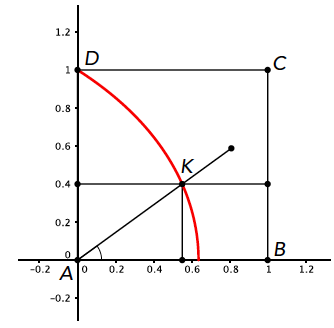
Wat is de $y$-coördinaat op tijdstip $t$? Hier is het het handigst om naar de horizontale lijn te kijken. Die lijn stijgt in $1$ tijdseenheid helemaal omhoog tot $y = 1$, dus in $t$ tijdseenheden heeft de lijn afstand $t$ afgelegd. Dus $y = t$.

Voor de $x$-coördinaat is dat ietsje ingewikkelder. Op tijdstip $t$ is de hoek die de draaiende lijn maakt met de $x$-as gelijk aan $\frac{1}{2}πt$ (als we de hoek in radialen meten). Dat betekent dat we de $x$-coördinaat kunnen uitdrukken in $t$ met behulp van de tangens:

$$\tan(\frac{1}{2}\pi t)= \frac{y(t)}{x(t)}.$$

We kunnen de $t$ hieruit elimineren omdat we weten dat $y = t$. Dat betekent dat we kunnen schrijven:

$$\tan(\frac{1}{2}\pi y)= \frac{y}{x}.$$

Even herschrijven levert de volgende formule op:

$$x = y· \frac{1}{\tan(\frac{1}{2} y)},$$

oftewel: $x$ als een functie van $y$.

Geschiedenis

Maar waarom is deze specifieke kromme nou zo interessant? De kwadratrix werd al bestudeerd in de Griekse oudheid. Uit die tijd zijn drie beroemde constructieproblemen bekend: de verdubbeling van de kubus, de driedeling van de hoek en de kwadratuur van de cirkel. In alle drie de gevallen werd gevraagd naar een constructie van een bepaald object met passer en latje (een liniaal zonder schaalverdeling). Veel later werd bewezen dat dat voor alle drie de problemen niet kan. Maar al in de Griekse oudheid werden voor deze problemen wel alternatieve oplossingen gevonden, die gebruik maakten van andere hulpmiddelen dan passer en latje alleen. Eén zo’n oplossing gaat met de kwadratrix – deze oplossing geven we straks. Omdat zulke constructies niet met enkel een passer en een latje gedaan kunnen worden, tellen ze niet als oplossing volgens de strengste constructieregels.

De kwadratrix wordt al vermeld in het verzamelwerk van Pappos (ca. 290 - ca. 350). Pappos schrijft dat Deinostratos (ca. 390 - ca. 320 v. Chr.) en Nikomedes (ca. 280 - 210 v. Chr.) de kwadratrix gebruikten om de kwadratuur van de cirkel op te lossen. Uit andere bronnen weten we dat ook Hippias van Elis (geboren ca. 450 v. Chr.) de kromme gevonden had.

De oude Grieken definieerden de beweging van de kwadratrix overigens precies tegenovergesteld: de draaiende lijn begint op $AD$ en draait naar $AB$ en de horizontale lijn beweegt omlaag. De definitie hierboven levert natuurlijk dezelfde kromme op, en is voor ons net wat handiger in het gebruik.

Driedeling van de hoek

We beginnen met de driedeling van de hoek, want die constructie is eenvoudig met behulp van de kwadratrix, in ieder geval voor hoeken kleiner dan $90^\circ$.

Bij dit probleem gaat het erom een gegeven hoek in drie gelijke delen te verdelen. Met de kwadratrix lukt dat inderdaad. Hoe? Kijk maar naar figuur 3. Gegeven is een hoek $α$. Leg die hoek in de kwadratrix met één been op de $x$-as en het andere been in het eerste kwadrant. Dan vinden we een punt op de kwadratrix waar dat tweede been doorheen gaat. Dat punt noemen we $P$. Punt $Q$ is het punt op de $y$-as op dezelfde hoogte als $P$.

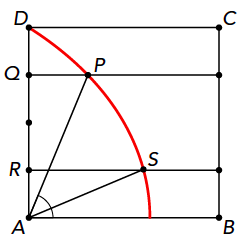
Nu gaan we lijnstuk $AQ$ in drie gelijke delen verdelen.

Opgave 1. Probeer zelf uit te vinden hoe je een gegeven lijnstuk met alleen passer en latje in drie gelijke delen kunt verdelen. (Kom je er niet uit, lees dan de hint aan het eind van dit stuk.)

Punt R ligt op de y-as op een derde van lijnstuk $AQ$. Op dezelfde hoogte ligt ook een punt op de kwadratrix; noem dat punt $S$. Als het r tijdseenheden duurt om punt $P$ te bereiken als je de kwadratrix maakt door de hierboven beschreven beweging, dan duurt het dus precies $\frac{1}{3} r$ tijdseenheden om bij punt $S$ te komen. Dat wil zeggen dat hoek $SAB$ precies $\frac{1}{3}$ is van hoek $PAB$, en dat was de gegeven hoek.

De oude Grieken konden de driedeling van de hoek overigens ook op een aantal andere manieren oplossen. Zie bijvoorbeeld ‘De onmogelijke driedeling’ van Wendy Ellens in Pythagoras 46-6 (juni 2007) en ‘Hoeken delen met Archimedes en Abe’ van Luuk Hoevenaars in Pythagoras 54-6 (juni 2015).

Kwadratuur van de cirkel

Het probleem van de kwadratuur van de cirkel vraagt bij een gegeven cirkel om een passer-en-latje-constructie van een vierkant met dezelfde oppervlakte als de gegeven cirkel. Als de straal van de cirkel $1$ is, komt dit dus neer op het construeren van een lijnstuk met lengte $\sqrt{\pi}$. Alleen met passer en latje lukt dit niet, maar met behulp van de kwadratrix wel.

Om in te zien wat de kwadratrix met de kwadratuur van de cirkel te maken heeft, maken we gebruik van de formule hierboven:

$$x =y· \frac{1}{\tan(\frac{1}{2}\pi y)}.$$

Het punt waar de constructie van uit gaat, is een punt dat eigenlijk niet bestaat: het punt van de kwadratrix dat op de $x$-as lijkt te liggen. Waarom lijkt te liggen? Nou, als $y$ gelijk aan $0$ is, oftewel als $t = 0$, dan vallen de draaiende en de stijgende lijn allebei samen met lijn $AB$ en is er dus niet slechts één snijpunt. Op dat moment is het punt op de kwadratrix dus niet gedefinieerd.

De moderne wiskunde heeft ons echter een nuttig begrip gebracht dat de oude Grieken nog niet kenden: de limiet. We kunnen kijken wat er gebeurt met onze formule voor $x$ als we $y$ naar $0$ laten gaan:

$$\lim_{y\to 0} x = \lim_{y\to 0} y· \frac{1}{\tan(\frac{1}{2}\pi y)} .$$

Het is nu net wat handiger om over te schakelen op een andere variabele $u = \frac{1}{2}πy$. Dan is

$$y = \frac{2}{\pi}u$$

en krijgen we

$$\lim_{u\to 0} \frac{2}{\pi}u· \frac{1}{\tan u} =$$

$$\lim_{u\to 0} \frac{2}{\pi}u· \frac{\cos u}{\sin u}=$$

$$\lim_{u\to 0} \frac{2}{\pi}· \frac{1}{\frac{\sin u}{u}}·\cos u.$$

Omdat

$$\lim_{u\to 0} \cos u =1$$

en ook de standaardlimiet

$$\lim_{u\to 0} \frac{\sin u}{u}=1,$$

vinden we nu

$$\lim_{y\to 0} x = \frac{2}{\pi}.$$

Het niet-bestaande ‘snijpunt’ van de kwadratrix met de $x$-as is dus het limietpunt $(\frac{2}{\pi}, 0)$.

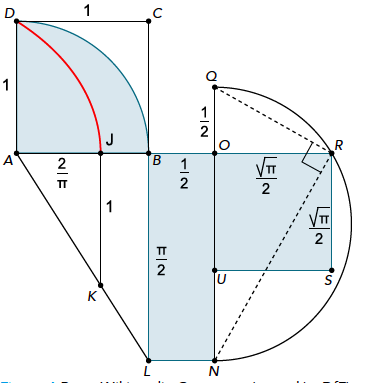
Nu hebben we dus een lijnstuk van lengte $\frac{2}{\pi}$ gevonden, door uitgaande van een lijnstuk van lengte $1$ de betreffende kwadratrix te tekenen en het limietpunt te nemen op de $x$-as. En vanuit een lijnstuk van lengte $\frac{2}{\pi}$ is het inderdaad mogelijk om een lijnstuk van lengte $\sqrt{\pi}$ te construeren! De oplossing daarvoor vind je in figuur 4. Aan de hand van de volgende opgaven kun je zelf controleren dat je vanuit deze kwadratrix inderdaad de kwadratuur van de cirkel kunt oplossen, omdat je verder alles met passer en latje kunt afmaken.

Opgave 2. Uitgaande van het lijnstuk $AJ$ met lengte $\frac{2}{\pi}$ wordt lijnstuk $BL$ van lengte $\frac{\pi}{2}$ geconstrueerd. Leg uit hoe dat inderdaad kan met alleen passer en latje en controleer dat $BL$ inderdaad lengte $\frac{\pi}{2}$ heeft.

Opgave 3. Vervolgens wordt rechthoek $LNOB$ geconstrueerd met zijde $\frac{1}{2}$ . Hoe kun je die lengte van $\frac{1}{2}$ hier vinden met passer en latje en hoe kun je de rechthoek verder construeren?

Opgave 4. Vervolgens wordt lijnstuk $ON$ aan de kant van $O$ verlengd met $\frac{1}{2}$ en wordt de halve cirkel op diameter $NQ$ getekend. Maak zelf deze constructie ook.

Opgave 5. Lijnstuk $AB$ wordt verlengd tot het de cirkel snijdt, het snijpunt noemen we $R$. Nu begint het interessantste deel van de opgave: lijnstuk $OR$ heeft nu lengte $\frac{1}{2}\sqrt{\pi}$. Bewijs dat dat inderdaad zo is. (Zie ook de hint hieronder.)

In figuur 4 is de oppervlakte van vierkant $USRO$ dus gelijk aan die van de kwart cirkel in vierkant $ABCD$. En daarmee is de kwadratuur van de cirkel inderdaad opgelost, mits je de kwadratrix toestaat als hulpmiddel.

Hint bij opgave 1. Teken loodrecht op een uiteinde van je gegeven lijnstuk een lijnstuk dat drie keer zo lang is als het gegeven lijnstuk en gebruik gelijkvormige driehoeken.

Hint bij opgave 5. Merk op dat de hoek bij $R$ recht is vanwege de stelling van Thales. Gebruik dat gegeven om aan te tonen dat driehoek $QOR$ gelijkvormig is met driehoek $RON$.