In de verzekeringswiskunde, ook wel actuariaat genoemd, zijn binnen het onderdeel levensverzekeringswiskunde de zogeheten AG-tafels in gebruik. Ze zijn nodig bij het berekenen van koopsommen (eenmalige betalingen) en premies van
levensverzekeringen zoals kapitaalverzekeringen (uitkeringen 'bij leven'), overlijdensverzekeringen en pensioenberekeningen. Het AG is het Actuarieel Genootschap, dat deze tabellen eens in de vijf jaar maakt met behulp van sterftegegevens
van het CBS, het Centraal Bureau voor de Statistiek. De basis van de AG-tafels zijn de kansen op overleving van jaar tot jaar. De overlevingsfunctie $\ell_x$ speelt hierin een grote rol. De functie $\ell_x$ is gedefinieerd als het aantal levende personen van $x$ jaar oud, met een (fictieve) startwaarde van 0-jarigen. Zo stelt bijvoorbeeld $\ell_{65}/\ell_{30}$ de overlevingskans voor van een 30-jarige man of vrouw om 65 te worden. (Er zijn in de levensverzekeringswereld twee soorten
$\ell_x$-tabellen: voor mannen en voor vrouwen.) In de loop der tijd zijn diverse modellen voor de functie $\ell_x$ gebruikt, onder andere door Graunt (1661), De Moivre (1725), Gompertz (1825) en Makeham (1860). 

De AG-tafels zijn gebaseerd op de overlevingsfunctie van Makeham, met enkele aanpassingen. Het vakgebied van de verzekeringswiskunde is overigens deels te danken aan raadpensionaris Johan de Witt, die in 1671 liet zien hoe je de koopsom van bijvoorbeeld een 'lijfrente' (letterlijk: 'rente', d.w.z. uitkeringen op eigen 'lijf', dus bij leven) of overlijdensverzekering kon berekenen met behulp van sterfte- en overlevingskansen uit het recente verleden.

Velen beschouwen de Engelsman Graunt als de eerste die een (empirische) overlevingsfunctie voorstelde. We zullen in dit artikel laten zien dat Cardano in Italië al een eeuw eerder (in 1560) een overlevingsfunctie $\ell_x$ opstelde.

(HistorisChe) overlevingsfunCties

Een overlevingsfunctie is een formule, al dan niet gebaseerd op theoretische argumenten, die overleving/sterfte van een bevolking kwantitatief vastlegt. In tabel 1 zie je de overlevingscijfers die John Graunt publiceerde in 1661 (bekend als de 'London life table'). 

Tabel 1

Age		$0$		$6$		$16$		$26$		$36$		$46$		$56$		$66$		$76$
Survivors		$100$		$64$		$40$		$25$		$16$		$10$		$6$		$3$		$1$

Dit is de eerste (proefondervindelijke) overlevingsfunctie $\ell_x$. In later jaren zocht men naar een formule, die zo goed mogelijk bij de praktijk paste. Abraham de Moivre stelde in 1725 een eenvoudige, dalende lineaire functie voor, met startwaarde 86: 

$$\ell_x=86-x.$$

Later volgde de overlevingsfunctie van Benjamin Gompertz:

$$\ell_x = k\cdot g^{c^x}.$$

Hierin zijn $k$, $g$ en $c$ drie nog te bepalen parameters. Let op: het gaat hier grondtal $g$ tot de macht ($c$ tot de macht $x$). Verder geldt: $k > 0$, $0 < g < 1$ en $c > 1$. 

In de huidige praktijk van levensverzekeringen wordt gebruik gemaakt van de formule van William Makeham:

$$\ell_x=k\cdot s^x\cdot g^{c^x}.$$

Deze overlevingsfunctie kent vier parameters: $k$, $s$, $g$ en $c$. Ze zijn onder andere gebaseerd op de eerder genoemde sterftegegevens van het CBS, de steeds nog stijgende overlevingskansen van Nederlanders en een techniek die de losse data 'wiskundig gladstrijkt'. (We gaan op de technische achtergrond van deze formule in dit artikel verder niet in.) In figuur 1 zijn de grafieken weergeven van de overlevingsfuncties van Graunt, Gompertz (met $k = 100{,}1$; $g = 0{,}999$ en $c = 1{,}1$) en Makeham (met $s = 0{,}999$). Voor de overzichtelijkheid is $\ell_0 = 100$ gekozen voor de modellen van Gompertz en Makeham (in de praktijk worden daar andere startwaarden voor gekozen).

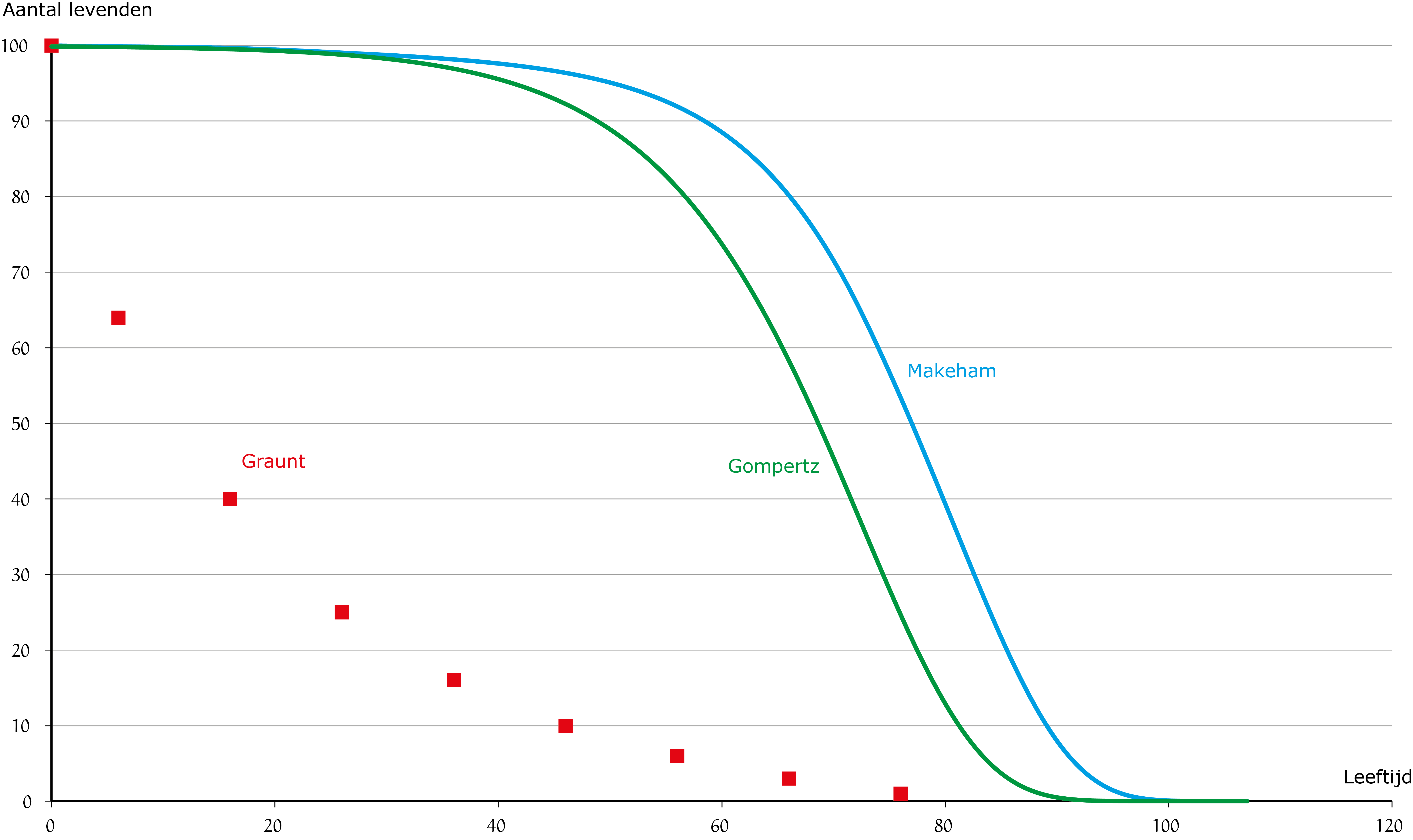
Opgave 1 Bereken de coördinaten van het buigpunt van $\ell_x = 100{,}1 \cdot 0{,}999^{1{,}1^x}$, de overlevingsfunctie van Gompertz. Check deze coordinaten in de grafiek.

Geronimo Cardano

Geronimo Cardano, ook bekend als Gerolamo Cardano (1501-1576), was, zoals zoveel van zijn tijdgenoten, een veelzijdig wetenschapper: natuurkundige, astroloog, wiskundige en filosoof. In 1526 behaalde hij een doctorstitel in de medicijnen.
Cardano is het meest bekend om zijn methode ter oplossing van derdegraadsvergelijkingen (met Tartaglia). Ook hield hij zich al bezig met het imaginaire getal $i$, de wortel uit $-1$. Verder is bekend dat hij zeer goklustig was en een regelmatig
cafébezoeker. In 1566 publiceerde hij Liber de Ludo Alea ('The Book on Games of Chance'). In dit boek suggereert hij een model voor de 'gemiddelde resterende levensduur'. We zullen dit model de 'levensverwachtingsfunctie van Cardano' noemen. 

Cardano’s levensverwachtingsfunctie

Cardano stelde om te beginnen vast dat hij niemand ouder dan 85 kende. Verder nam hij aan dat elk jaar de resterende levensduur ('levenskracht' noemde hij dit) met een vaste factor $\frac{39}{40}$ afneemt. Helaas geeft Cardano geen verklaring van de waarde van de factor $\frac{39}{40}$. Uiteraard wordt de levenskracht elk jaar verminderd met $1$. We krijgen zo het volgende model:

$$L(x+1)=\frac{39}{40}\cdot L(x)-1 \mbox{   met }L(85) = 0.$$

Hierin stelt $L(x)$ de (resterende) levensverwachting op leeftijd $x$ voor. 

Voor de oplossing van deze differentievergelijking (iteratieve vergelijking), de levensverwachtingsfunctie $L(x)$ moeten we eerst 'lineariseren'.

Stel daartoe $y(x) = L(x) + 40$. Dan is het oorspronkelijke model te schrijven als:

$$y(x 1)=\frac{49}{50}\cdot y(x) \mbox{   met }L(85)=40.$$

Opgave 2 Los deze iteratieve vegelijking op en vind daarmee $L(x)$. Lees dan pas verder. Tip: probeer $y(x) = c\cdot g^x$.

De oplossing is:

$$L(x)= 344\cdot \left(\frac{39}{40}\right)^x- 40.$$

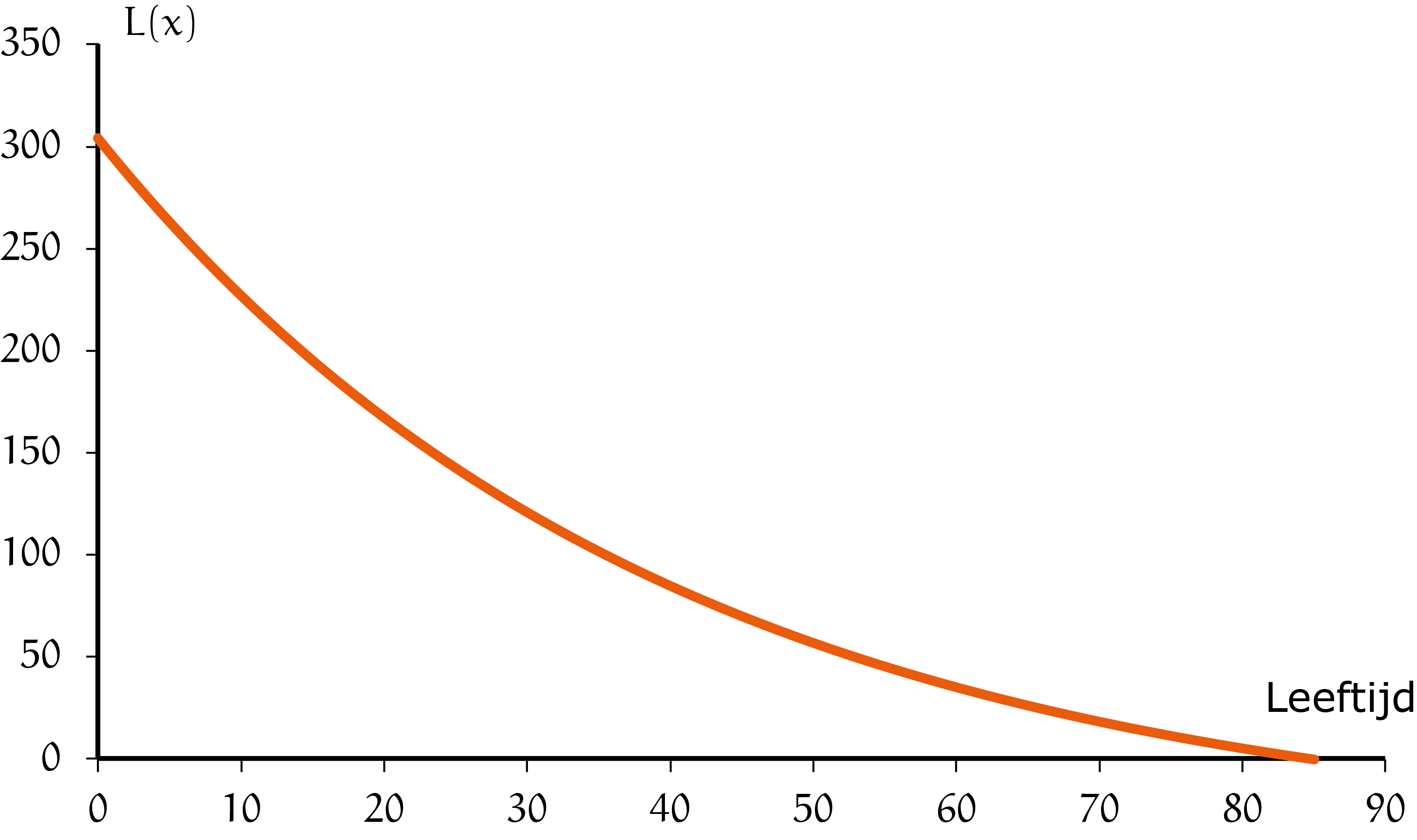
Dit is een dalende exponentiële functie met de hoopgevende eigenschap dat de 'levenskracht' van een 0-jarige gelijk is aan $L(0) = 304$ jaar. Een aantal volgende (afgeronde) waarden zijn: $L(1) = 295$, $L(2) = 287$, $L(3) = 279$. De 'levenskracht' neemt in deze jaren volgens Cardano dus met $8$ à $9$ per jaar af. Zie de grafiek in figuur 2. Helaas is deze $L(x)$-functie niet erg realistisch, zoals we straks zullen zien. 

Relatie tussen $\ell_x$ en $L(x)$

De levensverwachtingsfunctie van Cardano is niet rechtstreeks te vergelijken met een overlevingsfunctie. Er bestaat wel de volgende relatie tussen $\ell_x$ en $L(x)$:

$$L(x)=1\cdot\frac{\ell_{x+1}}{\ell_x} + 1\cdot\frac{\ell_{x+2}}{\ell_x} + \cdots + 1\cdot \frac{\ell_{\omega}}{\ell_x} = \frac{\ell_{x+1}+\ell_{x+2}+\ell_{\omega}}{\ell_x}.$$

$(1)$

(Het symbool $\omega$ staat voor het hoogste leeftijd in een $\ell_x$-tabel, in Nederland nu rond de $115$ jaar.) Elke term stelt hierin een levensjaar ('$1$') voor en de bijbehorende kans daarop ten opzichte van levensjaar $x$. Uit bovenstaande relatie volgt echter ook:

$$\frac{\ell_{x+1}}{\ell_x} = \frac{L(x)}{L(x+1)+1}.$$

$(2)$

 

En daarmee tevens − omdat de eenjarige overlevingskans $\frac{\ell_{x+1}}{\ell{x}}$ kleiner is dan $1$:

$$L(x)-L(x+1)\le 1.$$

$(3)$

Opgave 3 Bewijs $(2)$ en $(3)$ uit eigenschap $(1)$

In woorden: twee opeenvolgende (resterende) levensduren mogen niet meer dan $1$ verschillen. Aan deze eigenschap voldoet de $L(x)$-functie van Cardano niet, immers in de 'beginjaren' verschillen ze $8$ à $9$ jaar.

Opgave 4 Ga na dat bijvoorbeeld $L(x + 1) = 0{,}99 \cdot L(x) - 0{,}25$ met $L(85) = 0$ als variant op de levensverwachtingsfunctie van Cardano wel aan $(2)$ en $(3)$ voldoet.

Natuurlijk kunnen we ook voor de andere $\ell_x$-functies de bijbehorende overlevingsfuncties $L(x)$ vinden. Redelijk eenvoudig kan worden aangetoond dat de lineaire $\ell_x$-functie van De Moivre ook een lineaire $L(x)$ geeft:

$$L(x)=42\tfrac{1}{2}-\tfrac{1}{2}x.$$

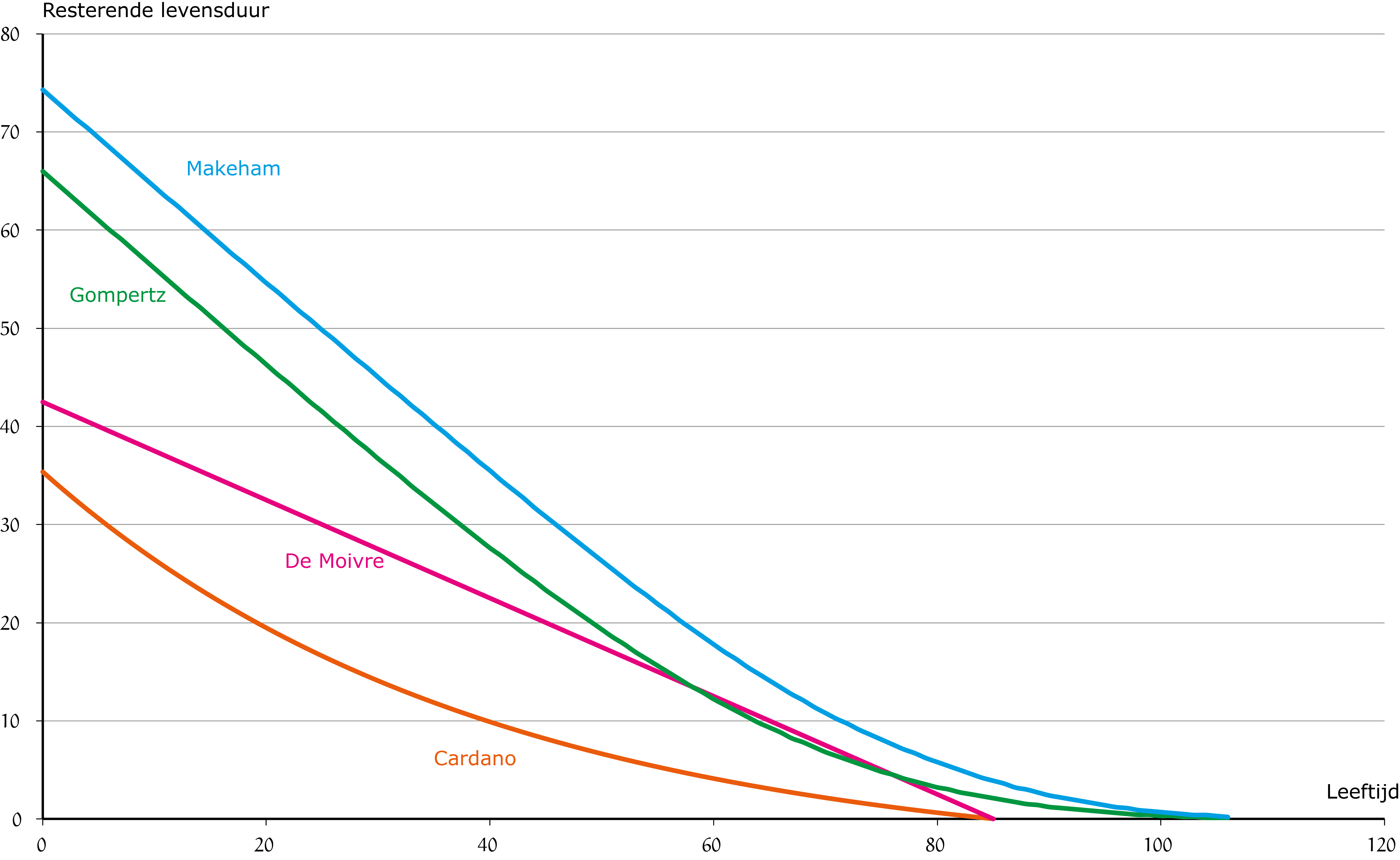
Tot slot staan in figuur 3 de $L(x)$-funties van Cardano, De Moivre, Gompertz en Makeham bij elkaar afgebeeld.