In de beginjaren tachtig van de vorige eeuw lag de Rubikskubus in alle speelgoedwinkels over de hele wereld. De draaipuzzel met kleurige vakjes, bedacht door de Hongaar Ernő Rubik, werd een enorme rage. De originele kubus heeft afmetingen 3 × 3 × 3, maar later werden ook kubussen van 4 × 4 × 4 en van 5 × 5 × 5 op de markt gebracht. Het is trouwens de gewoonte om, ondanks het feit dat een kubus een driedimensionaal object is, van een 3 × 3-kubus (of 4 × 4, of 5 × 5) te spreken. Het doel van de puzzel is natuurlijk om rijen blokjes zo te draaien, dat je uiteindelijk een kubus met zes egale zijvlakken overhoudt.

Als je zomaar wat draait, kan het uren duren voor je de puzzel hebt opgelost. Maar puzzelaars zijn erin geslaagd om een algemene methode op te schrijven om de Rubikskubus op te lossen. In 1982 werd voor het eerst een wereldkampioenschap gehouden. Winnaar was de Amerikaan Minh Thai, met een tijd van 22,95 seconden. De Nederlander Guus Razoux Schulz werd met 24,32 seconden tweede.

Na aan aantal jaren van ongekende populariteit verloren mensen het plezier in de Rubikskubus, maar rond de eeuwwisseling, toen puzzelaars elkaar via het internet konden vinden, beleefde de kubus een wederopstanding. In 2003 richtten de Nederlander Ron van Bruchem en de Amerikaan Tyson Mao de World Cube Association op, een organisatie die wedstrijden organiseert voor het zo snel mogelijk oplossen van een Rubikskubus. Voor het eerst sinds 1982 werd er weer een wereldkampioenschap gehouden.

In dit artikel kijken we naar een 2 × 2-kubus, de zogeheten pocketkubus. Alhoewel deze er simpel uitziet – zeker naast een gewone Rubikskubus –, valt dit in de praktijk erg tegen. Ondanks het kleine formaat is de puzzel nauwelijks op te lossen door gewoon maar wat te proberen. Hoe kan dat? Daar gaan we proberen achter te komen!

De pocketkubus bestaat uit 8 blokjes, die we corners noemen. Elke corner heeft 3 stickers. De configuratie van de puzzel wordt vastgelegd doortwee aspecten: de permutatie van de corners (de positie van de corners ten opzichte van elkaar) en de oriëntatie van de corners (de draaiing ervan). De puzzel is pas opgelost als alle stukjes in de correcte permutatie en oriëntatie zitten. We gaan nu uitrekenen hoeveel mogelijke posities er zijn op een 2 × 2-kubus. We beginnen met de permutaties.

Permutaties

Er geldt:

Stelling 1. Iedere willekeurige permutatie van de corners is oplosbaar.

Anders gezegd: het is altijd mogelijk om alle corners op de juiste plaats te krijgen, ongeacht de beginpositie waarin ze zitten.

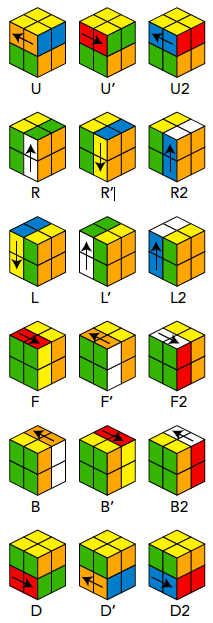
Om dit te bewijzen, voeren we wat notatie in (zie ook de illustratie op de volgende pagina). We noteren het topvlak van de kubus met de letter U (van up). We noteren het rechtervlak met R, het linkervlak met L, het vlak aan de voorkant met F (front), het vlak aan de achterkant met B (back), en het vlak aan de onderkant met D (down). Nu noteren we een rotatie van het topvlak 90° met de klok mee als U. Een rotatie van het topvlak 90° tegen de klok in noteren we als U’, en een rotatie van 180° noteren we als U2. Met deze notatie kunnen we compact een zettenreeks (met een sjiek woord: algoritme) opschrijven. We zullen een rotatie van een vlak een zet noemen. Om een corner aan te duiden, gebruiken we de drie letters van de vlakken waarin de corner zit.

We gaan nu bovenstaande bewering bewijzen. Beschouw de zettenreeks

R U2 R’ U’ R U2 L’ U R’ U’ L

Dit algoritme verwisselt corners URF en URB, terwijl alle andere corners op hun plaats blijven. We kunnen aannemen dat één corner al meteen op zijn plaats zit (en zelfs goed gedraaid) zit. Merk op datwe dan meteen van alle andere corners weten waar ze naartoe moeten. Om dit voor elkaar te krijgen, kunnen we de blokjes één voor één (met behulp van het algoritme) naar hun juiste positie manoeuvreren, door steeds de kubus te roteren.

We willen echter voorkomen dat we stukjes die al op hun plaats zitten, verkeerd zetten. Om dit te doen moeten we voor ieder stukje een route vinden die niet langs stukjes gaat die we al geplaatst hebben. Dit is echter niet moeilijk: het makkelijkst is om eerst een laag helemaal op zijn plaats te zetten. En daarmee hebben we de bewering bewezen.

Aantal permutaties

Je denkt misschien dat er 8! = 40.320 verschillende permutaties zijn. Dit is echter niet zo, omdat er ook nog rotaties bij betrokken zijn. Bijvoorbeeld, het algoritme R L’ komt simpelweg overeen met een rotatie van de gehele kubus. (Dit is overigens alléén op een 2 × 2-kubus het geval. Op een 3 × 3-kubus is R L’ niet alleen een rotatie.)

Als we een positie hebben en de kubus alleen maar roteren, hebben we 6 keuzes voor het U-vlak en daarna nog 4 keuzes voor het F-vlak, dus we kunnen 6 · 4 = 24 posities bereiken door alleen maar rotaties. (We kunnen ook zeggen: het hoekstuk dat we vast zetten, heeft 8 mogelijke posities en 3 rotaties, dus zijn er 8 · 3 = 24 mogelijke rotaties die opgelost zijn.) Omdat we rotaties als dezelfde positie beschouwen, houden we voor het aantal mogelijke permutaties 8!/24 = 1.680 over.

Oriëntatie

Nu kijken we naar de oriëntatie. Hier blijkt wel een restrictie te zijn.

Er geldt:

Stelling 2. Er bestaat géén algoritme om op een 2 × 2-kubus alleen maar een corner te draaien.

Met andere woorden: als we de oriëntatie van 7 corners weten, ligt de oriëntatie van de laatste vast.

Hoe bewijzen we deze stelling? We introduceren het draaigetal van een configuratie als volgt. Op een kubus met normaal kleurenschema ligt wit tegenover geel (ik ga er vanaf nu vanuit dat dat het gevalis). Iedere corner heeft dus ofwel een witte sticker, ofwel een gele sticker, maar nooit allebei.

Veronderstel dat we een willekeurig algoritme hebben zonder rotaties, waarin we beginnen met het witte vlak op de bovenkant (merk op: een rotatie kunnen we schrijven als twee zetten, dus dit is zonder verlies van algemeenheid). We definiëren dan het draaigetal van een corner als volgt. Als de witte (of gele) sticker op het U- of D-vlak zit, heeft de corner draaigetal 0. Moeten we de corner met de klok mee roteren om de witte (of gele) sticker in het U- of D-vlak te krijgen, dan heeft deze draaigetal 1. Moeten we de corner tegen de klok in roteren, dan heeft deze draaigetal 2. Het draaigetal van de kubus definiëren we nu als de som van de draaigetallen van alle corners. In de beginsituatie is dit draaigetal bijvoorbeeld 0. We beweren dat het draaigetal altijd deelbaar is door 3.

Als we een zet met het U- of D-vlak doen, is het duidelijk dat het draaigetal gelijk blijft (de volgorde van de draaigetallen verandert alleen).

Nu beschouwen we de zet R. Merk op dat het draaigetal van de corners in het L-vlak niet verandert. We merken op dat het draaigetal van corner URF altijd met 1 mod 3 afneemt (dit is eenvoudig te controleren door gevalsonderscheiding), net als van de corner DRB. De draaigetallen van corner URB en DRF nemen altijd juist met 1 mod 3 toe. Hieruit volgt dat het draaigetal van de hele kubus verandert met +2 – 2 = 0 mod 3.

We kunnen nu alle andere zetten maken. Een F kunnen we maken met U’ D R U D’, en L en B op soortgelijke manier. We concluderen dat iedere zet het draaigetal invariant laat modulo 3, en aangezien het in de beginsituatie 0 is, is het altijd deelbaar door 3. Als er precies één corner gedraaid is, is het draaigetal 1 of 2, en dus niet deelbaar door 3. Daarmee is stelling 2 bewezen.

Zijn er nog meer beperkingen op het roteren van corners? Dit blijkt niet zo te zijn.

Stelling 3. Gegeven een zekere permutatie van de corners, zijn er 37 mogelijke oriëntaties van de corners.

Om dit te bewijzen, beschouwen we het algoritme

(R U R’ U’)2 D (U R U’ R’)2 D’.

Dit draait de twee corners DRF en DLF, waarvan een met de klok mee en een tegen de klok in. Op deze manier kunnen we weer alle corners een voor een goed draaien (net zoals we bij de permutatie alles goed zetten). Alleen de oriëntatie van de laatste corner kunnen we niet bepalen, maar deze ligt sowieso vast doordat het totale draaigetal gelijk aan 0 mod 3 moet zijn. We kunnen dus 7 corners vrij roteren (de achtste ligt erdoor vast) en dat geeft ons 37 mogelijke oriëntaties, waarmee we de stelling hebben aangetoond.

Het aantal mogelijke posities van de pocketkubus komt hiermee op 8!/24 · 37 = 3.674.160. Dat is verbazingwekkend veel voor een puzzel die er zo eenvoudig uitziet, en zorgt ervoor dat zelfs deze puzzel nauwelijks is op te lossen door simpelweg wat te proberen.

Aan de andere kant is deze puzzel, in tegenstelling tot de 3 × 3, wel op te lossen door gericht proberen. Als een laag helemaal is opgelost, zijn er nog maar 4!/4 · 33 = 162 mogelijk posities (als we U-rotaties niet meerekenen) voor de laatste laag: dat is op zich te doen met proberen, al zal het wel lang duren als je pech hebt...

We hebben nu ook meteen een algemene methode gevonden om iedere mogelijke positie weer op te lossen. Alhoewel we garantie hebben dat dit werkt, betekent dat niet dat het efficiënt is: met deze methode zal het totaal aantal zetten waarschijnlijk ver boven de honderd uitkomen. Een terechte vraag is dan natuurlijk: wat is het grootst mogelijke aantal zetten dat nodig is om de kubus op te lossen vanuit een zekere positie? Deze vraag is helaas veel moeilijker wiskundig te benaderen. De enige manier om dit op te lossen is met ‘brute force’, wat simpelweg neerkomt op alles narekenen. Het antwoord blijkt 10 zetten te zijn.