In het stuk ‘De pocketkubus’ in de vorige Pythagoras schreef ik over een minivariant van de beroemde Rubikskubus met acht blokjes. De alternating cube van Oskar van Deventer lijkt er een beetje op. De alternating cube is een 2 $\times$ 2-kubus, met de eigenschap dat de rotaties elkaar moeten afwisselen. Na een rotatie met de klok mee, moet een rotatie tegen de klok in volgen. Daarna moet weer een rotatie met de klok mee, dan weer tegen de klok in, enzovoort. De eerste rotatie is overigens met de klok mee.

Toen ik even vrij had van de competitie, was Antonie Paterakis, een van de snelste cubers ter wereld op 2 $\times$ 2, met de alternating cube aan het puzzelen. Hij slaagde erin om alle stukjes op de juiste plaats te krijgen, met alleen een paar verkeerd georiënteerde corners in de toplaag. Dat was Oskar zelf nog niet gelukt, dus al snel stonden we er met z’n allen naar te kijken. Het lukte echter maar niet om de laatste corners goed te oriënteren. Ook ik wist snel bijna alle stukjes goed te positioneren. Aangezien mij geen algoritmen bekend zijn met afwisselende ori.ntaties, moest ik er zelf een vinden. Een logisch begin is om herhaald bijvoorbeeld RU’ uit te voeren en te kijken wat er gebeurt. Na enig gepuzzel vond ik het volgende algoritme:

$$(R U’)3 y2 (R U’)3 z2 (R U’)3 x2 y’ (R U’)3 y.$$

De notaties R en U’ hebben we in het vorige nummer al ingevoerd. Op de volgende pagina zie je het notatieschema nogmaals. Met x schrijven we een rotatie alsof we met de hele kubus een L doen. Bij een y doen we met de hele kubus een U, bij een z doen we met de hele kubus een F.

Het bovengenoemde algoritme ori.nteert alleen de twee corners ULF en DLF. Op deze manier kunnen we dus, net als eerst, alle corners één voor één oriënteren, tot de laatste: deze zit automatisch goed. Uiteindelijk slaagden Antonie en ik erin om met dit algoritme de puzzel helemaal op te lossen.

Opgave. Waarom zit ook hier de laatste corner automatisch goed?

Toen Oskar deze puzzel voor het eerst toonde, vroegen de mensen op het Twisty Puzzles Forum (een forum voor draaipuzzels) zich meteen een aantal interessante dingen af. Hoeveel mogelijke posities zijn er? Hoeveel zetten zijn er nodig om de puzzel altijd op te kunnen lossen? Een andere mooie: is het mogelijk om de positie te maken die we normaal met U2 zouden maken (een zogenaamde ‘half turn state’)? Ik heb deze vraagstukken uitgewerkt, en kwam uit op de volgende conclusies.

Stelling 1. Er zijn voor de corners vanuit iedere permutatie $3^7 = 2.187$ mogelijke oriëntaties.

Dit blijkt uit het feit dat we met het algoritme dat ik had gevonden, twee naast elkaar liggende corners kunnen draaien, zonder verder iets te veranderen. De rest van het bewijs verloopt op dezelfde manier als bij een gewone 2 $\times$ 2-kubus (zie stelling 3 in mijn artikel in de vorige Pythagoras).

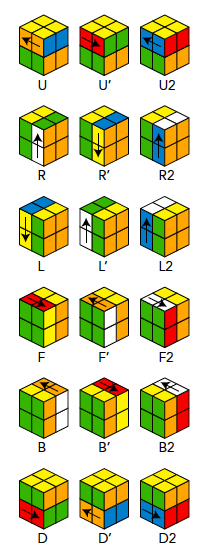
Notatie van de draaiingen aan een pocketkubus.
De toevoeging 2 betekent een draaiing over 180°.

Permutaties

Kennelijk ligt er geen nieuwe restrictie op de oriëntaties. Nu nog de permutaties. Het duurde vrij lang voordat ik hier een algemene methode voor had gevonden, maar het gebeurde regelmatig dat ik tijdens het puzzelen alle stukjes – toevallig – op hun plaats had gezet. Zoiets is alleen mogelijk als het aantal mogelijke permutaties klein is. En dat blijkt ook zo te zijn, want er geldt:

Stelling 2. Op rotaties na zijn er 14 verschillende permutaties mogelijk op de alternating cube.

Dit is te bewijzen door alles door te rekenen, maar we gaan het zoveel mogelijk zonder doen. Allereerst bedenken we ons dat ieder algoritme is te schrijven als een even lang algoritme met alleen R, U en F zetten (want een D is te zien als U y’, en zo ook voor B en L). Hierdoor blijft de corner DLB altijd op zijn plaats: er zijn dan nog 3 rotaties over (om de as door DLB en URF).

We beschouwen nu twee situaties: er is een even aantal zetten gedaan, of er is een oneven aantal zetten gedaan (vanuit de beginpositie). We beschouwen eerst het geval even. We kunnen dan kijken naar ‘zettenparen’: paren van een zet met de klok mee, en een tegen de klok in. We kunnen zo 3 $\times$ 2 = 6 paren maken (niet 3 $\times$ 3 = 9, omdat bijvoorbeeld U U’ niets verandert). We kunnen nu alle mogelijke algoritmes op de alternating cube maken door paren zetten achter elkaar te zetten, terwijl we ook altijd paren in iedere volgorde achter elkaar kunnen zetten: op deze manier hebben we dus niet meer de restrictie dat we maar een deel van de toegestane zetten op ieder moment mogen doen!

De combinatie van twee paren is altijd weer gelijk aan een paar. Dit kun je bewijzen door alle paren na te gaan, maar dat laten we hier wegens ruimtegebrek achterwege. We kunnen ons dus beperken tot de beginpositie, of hooguit een paar weg van de beginpositie. De positie na een paar is nooit gelijk aan die na een ander paar: ook dit kunnen we eenvoudig controleren. Op deze manier krijgen we dus 1 + 6 = 7 mogelijke posities (hier is de 1 voor de beginpositie en de 6 voor de positie na een paar).

Nu kijken we nog naar het geval met een oneven aantal zetten. Mijn eerste gok was hier: of 1 zet, of 3 zetten weg, dus 3 + 3 $\times$ 2 $\times$ 2 = 15 posities. Dit is echter fout, omdat er van deze posities een aantal hetzelfde zijn. We kunnen een slim trucje gebruiken om het juiste aantal te krijgen.

We beschouwen tijdelijk rotaties echt als verschillende configuraties. Beschouw nu een positie die een oneven aantal zetten vanaf de beginpositie is. Doe vanuit zo’n positie een U’. Dan belanden we in een positie met een even aantal zetten vanaf de beginpositie. Daarvoor zijn er 7 $\times$ 24 mogelijke posities (omdat we rotaties als verschillend beschouwen). Vóór de zet U’ zijn er dus ook 7 $\times$ 24 verschillende posities (inclusief rotaties). Exclusief rotaties zijn er dus (7 $\times$ 24)/24 = 7 mogelijke posities na een oneven aantal zetten. In totaal zijn er dus 7 + 7 = 14 mogelijke permutaties op de alternating cube.

De alternating cube van Oskar van Deventer. Links zie je het mechaniek. Als je één draai hebt gedaan, blokkeert het mechanisme een draai in dezelfde richting. Je kan wel terugdraaien. Op Youtube staan filmpjes waar dit goed is te zien:http://www.youtube.com/user/OskarPuzzle

Eenvoudiger?

Er zijn dus 14 $\times$ 2.187 = 30.618 mogelijke posities op de alternating cube. We kunnen nu ook gaan kijken: zit er een ‘half turn state’ bij? Het antwoord blijkt nee te zijn. Dit is het makkelijkst te bewijzen door te gebruiken dat er slechts 14 permutaties zijn. Uit controle blijkt dat geen van de permutaties overeen komt met die van een half turn state. Deze is dus onmogelijk.

Op basis van het aantal mogelijke posities zou je misschien denken dat de alternating cube veel eenvoudiger moet zijn dan de pocketkubus. Dat hoeft echter niet zo te zijn: de pocketkubus heeft veel meer zetmogelijkheden, waardoor het bijvoorbeeld veel eenvoudiger is om de ori.ntatie op te lossen. Ook kunnen we op een pocketkubus altijd twee corners omwisselen, dat kan bij de alternating cube niet. Omdat er nu zo weinig permutaties zijn, is het niet heel moeilijk om dat goed te krijgen. Waren er echter veel meer mogelijke permutaties geweest, dan is het waarschijnlijk moeilijker, omdat je minder vrijheid hebt. In het algemeen maken dit soort restricties een puzzel dan ook moeilijker om op te lossen.

Tot slot

Het is voor mij als wiskundige natuurlijk altijd leuk om dit soort puzzels wiskundig te benaderen, tot je een volledig beeld hebt van wat er allemaal (on)mogelijk is. Het geeft veel voldoening om uiteindelijk door te hebben hoe het nou zit. De keerzijde is dat het spelen daarn. ineens een stuk minder leuk is: je weet altijd waar je bent, je weet wat je moet doen, en de magie die het puzzelen ermee ooit had, is eigenlijk verdwenen.

Het is daarom geweldig dat er mensen als Oskar van Deventer zijn die telkens weer nieuwe puzzels weten te bedenken. Wie weet wat er nog uit deze nieuwe constructie die binnen in de alternating cube zit voor moois kan komen!

Hoe los je de alte rnati ng cube op?

Met de kennis die we hebben opgedaan bij het bepalen van het aantal posities, kunnen we nu ook een algemene oplossing geven voor het oplossen van de puzzel. We zullen hier overigens niet bewijzen dat deze methode werkt. Doe de volgende drie stappen.

Draairichting. Zorg ervoor dat de eerstvolgende zet die je moet doen met de klok mee is. Is dat niet zo, doe dan een willekeurige rotatie tegen de klok in, dan is de eerstvolgende zet weer wel met de klok mee.

Permutatie corners. Zoek twee corners op die naast elkaar zitten en ten minste twee kleuren gemeen hebben. (Nu zou het mogelijk moeten zijn om deze twee corners zo te draaien dat ze op elkaar aansluiten.) Zet deze twee corners op posities DLF en DLB. Deze twee corners laten we nu niet meer van plaats veranderen. Draai nu (in gedachten) de corners zo dat ze op elkaar aansluiten. We gaan rondom deze twee corners nu de rest van de puzzel oplossen. De oriëntatie van de kubus ligt door deze twee corners vast. Indien vanuit deze ori.ntatie gezien alle corners op de juiste plaats zitten, ga door naar de volgende stap. Doe anders herhaald R U’ tot alle corners op de juiste plaats zitten. Dit zou na maximaal 2 keer moeten gebeuren (want na 3 keer zit alles weer op de plek waar het oorspronkelijk zat). Gebeurt dit niet, dan is de puzzel niet oplosbaar. Lukt dit wel, ga dan door naar de volgende stap.

Oriëntatie corners. Met het algoritme dat we hadden gevonden, kunnen we twee naast elkaar liggende corners oriënteren. Los eerst alle corners in het D-vlak op (door iedere corner apart te draaien samen met de ernaast liggende corner in het Uvlak, gebruikmakend van het algoritme), daarna de twee overgebleven corners in het L-vlak (door ze te draaien samen met de corners in het R-vlak) en ten slotte corner URF. Nu zou de laatste corner, URB, ook opgelost moeten zijn. Is dat niet het geval, dan is de puzzel onoplosbaar.

De puzzel lijkt hiermee afgedaan: we weten het aantal posities en we hebben een algemene methode. Dit is echter allerminst het geval. We hebben bijvoorbeeld nog steeds niet bepaald wat het optimale aantal zetten is. Het is in principe mogelijk om dit met een computer uit te rekenen.

Maar ook: is het voor een mens mogelijk om in de buurt te komen van deze optimale oplossing? Ondanks dat de puzzel ‘slechts’ 30.618 posities heeft, is dat veel te veel om ze allemaal uit je hoofd te leren, met ook nog eens een bijbehorende oplossing bij iedere positie. Dit zorgt er echter juist voor dat kubussenwedstrijden nog interessant zijn.