De jury bestaande uit Klaas Pieter Hart (Technische Universiteit Delft), Sonja Cox (Universiteit van Amsterdam), en Matthijs Coster (Ministerie van Defensie) had het dit jaar niet moeilijk. Twee profielwerkstukken staken met kop en schouders uit boven de rest en net als vorig jaar vraag je je af hoe middelbare scholieren zo'n hoog niveau kunnen bereiken.

De twee winnende werkstukken waren niet te vergelijken: Nils van Veen en Lucas Joling schreven een degelijk profielwerkstuk over cryptologie, waarbij vooral het  originele slot de jury onmiddellijk over de streep trok. Het andere profielwerkstuk gaf een heldere en diepgaande analyse van de Riemannhypothese.

Het publiek van het Nederlands Mathematisch Congres was zeer onder de indruk: velen zeiden te hebben genoten van de heldere presentaties. Zij vonden beide  werkstukken even goed: hun stemmen staakten.

Cryptologie

Het profielwerkstuk Cryptologie van Nils van Veen en Lucas Joling van het Penta college CSG Scala in Spijkenisse heeft als onderwerp cryptologie, dat bestaat uit cryptografie en crypto-analyse. Nils van Veen en Lucas Joling hebben zich behoorlijk in de getallentheorie verdiept door literatuurstudie en ook door allerlei hoorcolleges te volgen op YouTube. De door hen gebruikte bronnen komen, goed gedocumenteerd vrijwel allemaal van internet.

De eerste tachtig pagina's van hun profielwerkstuk bestaan uit een degelijke expositie van de meest voorkomende systemen. Daar komen onderwerpen aan bod als elliptische krommen en de RSA-codering. Het is een helder en goed leesbaar geschreven stuk.

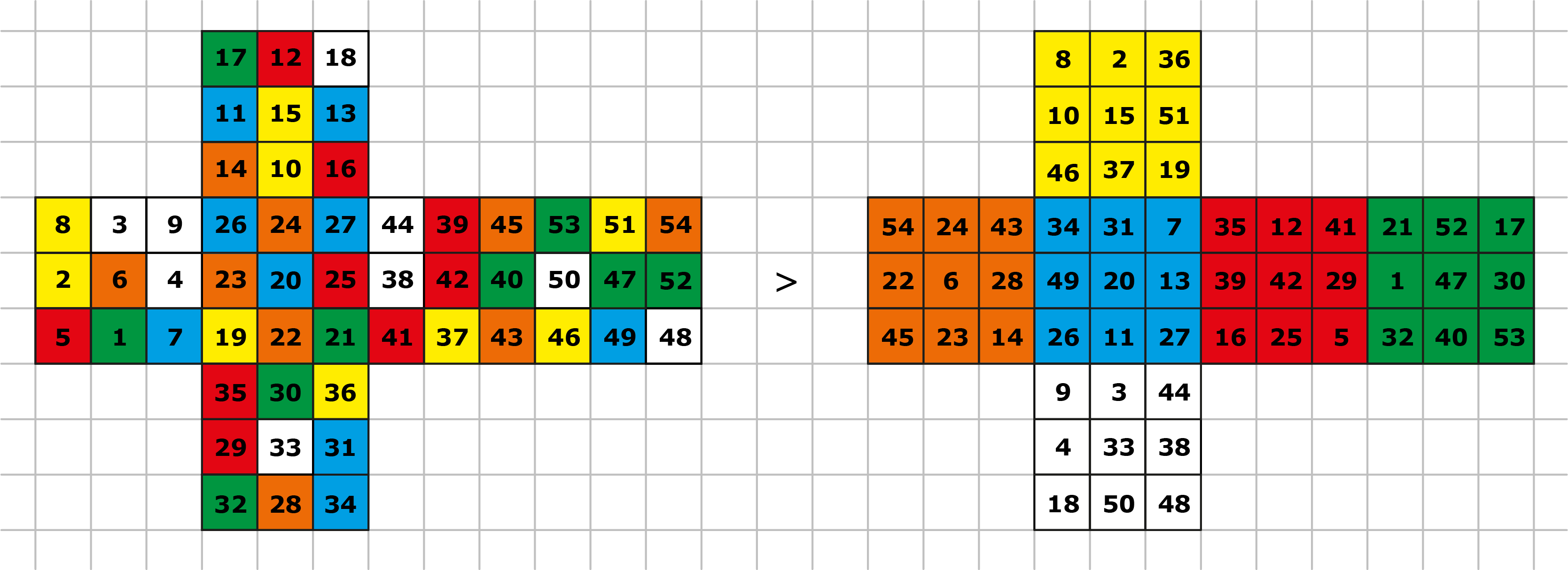
Echt interessant en origineel is het laatste hoofdstuk waar Nils en Lucas zelf een cryptografisch systeem opzetten. In dit hoofdstuk combineren ze de eenvoudige strategie van het Route-ciphering met de Rubik-kubus. In het kort gaat het algoritme zo: een Rubik-kubus wordt op een van te voren afgesproken manier in de war gebracht. Alle vlakjes van deze in de war gebrachte kubus worden op een eveneens van te voren afgesproken manier geordend. Het te versleutelen bericht wordt in deze volgorde op de kubus geplaatst. Daarna wordt de kubus verder in de war gebracht.

Om de boodschap op de kubus te kunnen lezen moet eerst de kubus worden opgelost en daarna op de voorafgesproken manier in de war worden gebracht. Het bericht is nu af te lezen via de vooraf afgesproken route. Dit kan je ook weer met grotere kubussen doen. De kans dat je de goede code bij toeval raadt, wordt gauw zeer klein.

Inzicht in de Riemann-hypothese

De andere eersteprijs-winnaar was Niels Kolenbrander van het Leo Kannercollege in Leiden. Niels hield een indrukwekkende en goed te volgen lezing over het buitengewoon moeilijke onderwerp de Riemannhypothese. Na een introductie zoals die ook in de epsilon-uitgave van Roland van der Veen en Jan van de Craats te vinden is, nam Niels ons mee naar speciaal op de verdeling van de priemgetallen toegesneden getaltheoretische functies.

Zijn profielwerkstuk geeft eerst een geschiedenis van de studie naar priemgetallen. Belangrijk in dit eerste deel zijn de functies $\pi(x)$, het aantal priemgetallen kleiner of gelijk aan $x$ en de logaritmische priemtel-functie $\psi(x)$ van Chebyshev, gegeven door:

$$\psi(x) = \sum_{p^{\alpha} \leq x,\\ p {\rm\ priem}} \ln (p),$$

die het aantal priemmachten kleiner of gelijk aan $x$ registreert.

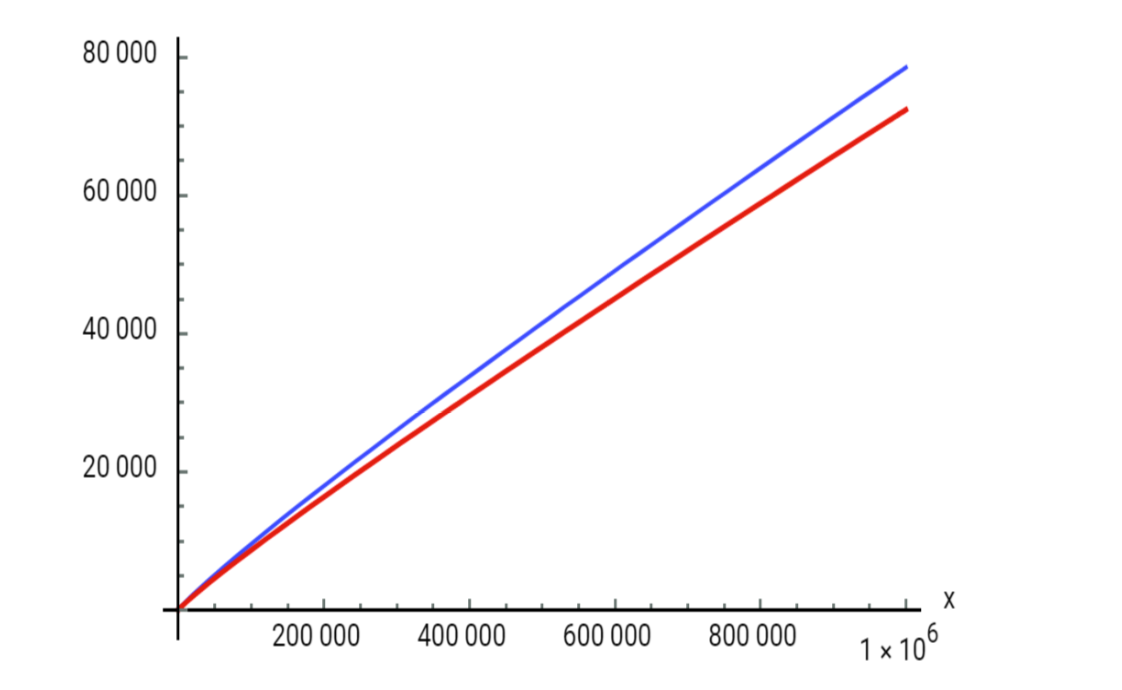
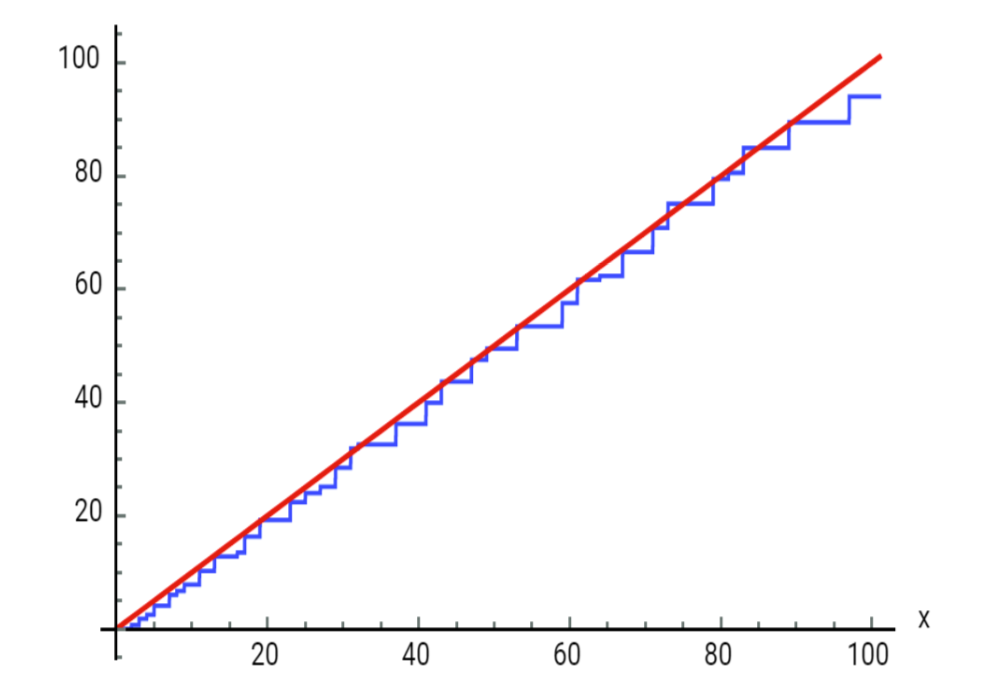
Beide functies vertonen asymptotisch gedrag zoals in de twee figuren is te zien. De eerste limiet

$$\lim_{x \rightarrow \infty} \frac{\pi(x)}{\left(\frac{x}{\ln x}\right)} = 1$$

die  bekendstaat als de priemgetalstelling, is bewezen in 1896 door Jacques Hadamard en Charles Jean de la Vallée-Poussin. De limiet

$$\lim_{x \rightarrow \infty} \frac{\psi(x)}{x} = 1$$

is hieraan equivalent.

Na deze inleidende hoofdstukken geeft Niels een prachtige expositie van de Riemann-zetafunctie. Bijna alles wat je bij het begrip van deze complexwaardige functie nodig hebt, legt hij uit. En passant leren we over contour-integratie, analytische voortzettingen, nulpunten en polen.

Uitzonderlijk is telkens de prachtige uitleg van de verschillende vergelijkingen uit de analytische getaltheorie. Niels blijft telkens stil staan bij de juiste details en brengt op deze manier bijvoorbeeld de Von Mangoldt-vergelijking tot leven. Wat een inzicht laat hij hier zien! Ik zou iedereen die in dit onderwerp geïnteresseerd is, willen aanraden dit profielwerkstuk te lezen. Het is niet gemakkelijk, maar met enige doorzetting krijg je er echt veel voor terug.

Internet

Deze twee profielwerkstukken zijn zeer verschillend. De manier waarop kennis en vaardigheden worden verworven heeft overeenkomsten.

Zowel Nils van Veen, Lucas Joling als Niels Kolenbrander hebben zich grote en gecompliceerde stukken wiskunde eigen gemaakt via internet: de eerste twee door het volgen van hele colleges op Youtube en de laatste door het bestuderen van openbare wiskundeteksten van universiteiten en Wikipedia-bronnen. Dat je daar zo'n niveau mee kan bereiken is ongelooflijk. Getalenteerde leerlingen (met flink wat doorzettingsvermogen) kunnen zich prima algebra, getallentheorie en complexe contour-integratie aanleren, om daarna wiskundige vakliteratuur op niveau te kunnen begrijpen. Het is bovendien inspirerend voor andere lezers, dat er scholen zijn die hun leerlingen daarin steunen