De opgave Laat $n$ een positief geheel getal zijn. Een sprinkhaan staat op de getallenlijn op het getal $1$ en mag telkens ofwel een sprong maken van lengte $2$, ofwel van lengte $3$. De sprinkhaan moet telkens landen op een geheel getal van $1$ tot en met $n$ waar de sprinkhaan nog niet eerder geweest is. De sprinkhaan wil graag alle gehele getallen van $1$ tot en met $n$ precies eenmaal bezoeken en eindigen op het getal $n$. Bewijs dat dit kan voor alle $n \ge 9$.

Op het eerste gezicht lijkt deze opgave erg ingewikkeld. Voor een gegeven getal $n \ge 9$ is het helemaal niet duidelijk hoe de sprinkhaan zo’n reeks van sprongen van $1$ naar $n$ zou kunnen maken, en het zoeken naar zo’n reeks lijkt eveneens geen gemakkelijk probleem. Hoe zorgen we ervoor dat we helemaal bij $n$ komen, zonder ook maar één tussenliggend getal over te slaan? De vreemde spronglengtes van de sprinkhaan helpen ook niet bepaald mee; hoe beginnen we aan zo'n opgave?

Zoals bij veel olympiadeopgaven, is het hier een goed idee om de complexiteit van het probleem zoveel mogelijk te reduceren door niet direct te kijken naar de tocht van de sprinkhaan voor algemene $n$, maar in plaats daarvan eerst de kleinst mogelijke waarden voor $n$ te proberen. Misschien kunnen we het probleem voor deze kleine waarden wél oplossen, en dit geeft ons misschien waardevolle inzichten voor het algemene geval. Wat is de kleinste waarde voor n die we kunnen kiezen? De opgave heeft het over $n \ge 9$, maar dat zijn al best grote en ingewikkelde gevallen. Misschien kunnen we deze voorwaarde beter even negeren en nog kleinere waarden voor $n$ kiezen; een beetje eigenwijs dus, maar daardoor wel makkelijker!

Voor $n = 1$ is er niets te doen, dus dit bijzondere geval voldoet formeel gezien. Maar voor $n = 2$ is er voor de sprinkhaan geen sprong mogelijk, dus dat geval kan niet. Voor $n = 3$ kan de sprinkhaan nooit naar het getal $2$ springen, dus dat geval kan ook niet. We gaan verder met $n = 4$; de sprinkhaan mag niet direct naar het einde springen, dus zijn eerste sprong moet wel naar het getal $3$ zijn, maar dan zijn er geen sprongen meer mogelijk. Het geval daarna, $n = 5$, is wat subtieler, maar omdat de sprinkhaan op het getal $5$ moet eindigen, kan hij het getal $3$ enkel bereiken vanaf het getal $1$, waarna hij gedwongen direct door moet springen naar het getal $5$ op het eind; opnieuw is het dus niet mogelijk. Het begint er bijna op te lijken dat het de sprinkhaan nooit zal lukken!

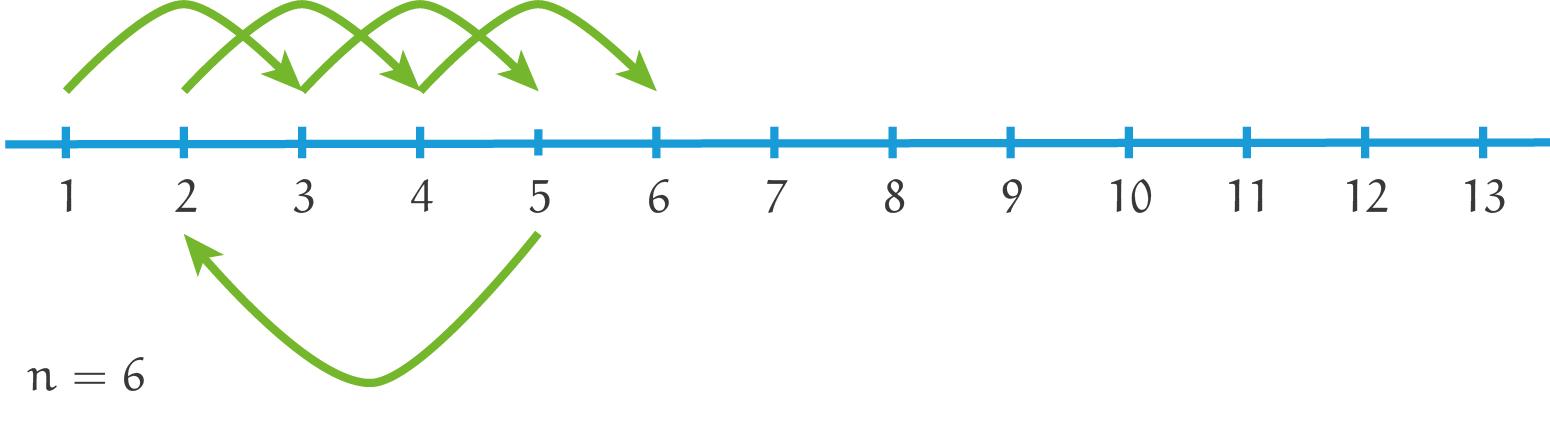
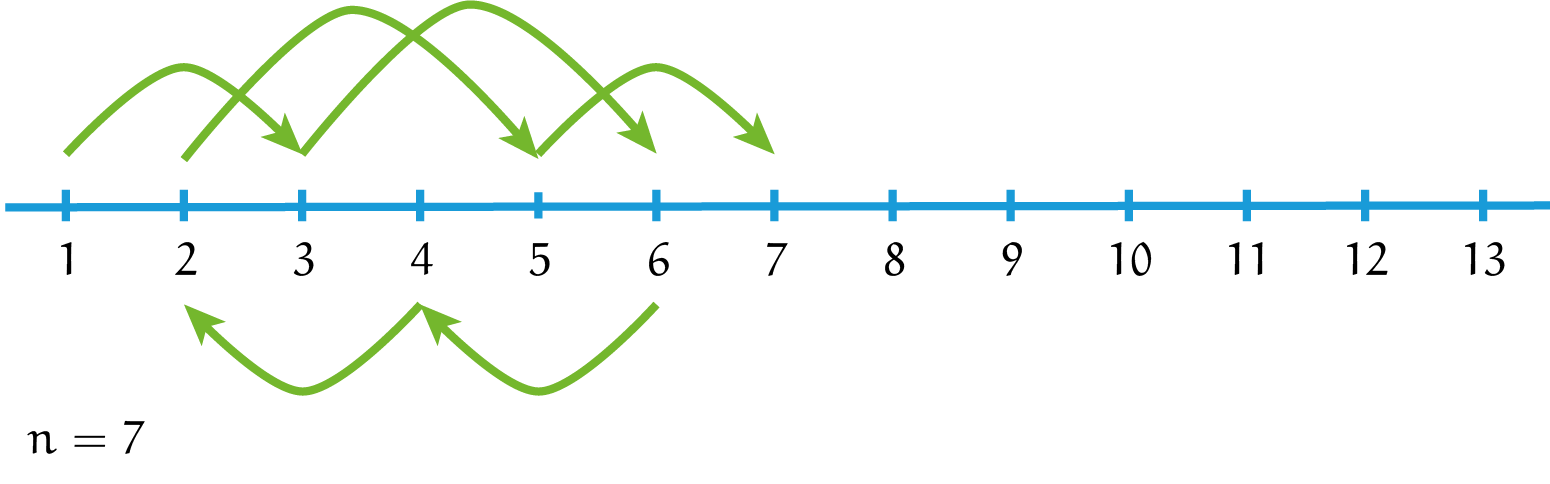
Met wat doorzettingsvermogen komen we zo aan bij het geval $n = 6$, en we vinden dan bijvoorbeeld de volgende reeks sprongen: $1-3-5-2-4-6$. In dit geval kan de sprinkhaan zijn wensen dus wel vervullen! Ook al hoeven we het alleen te bewijzen voor $n \ge 9$, blijkbaar geldt het ook voor $n = 6$. Hoe zit het met $n = 7$? Wat proberen levert dan bijvoorbeeld de reeks $1-3-6-4-2-5-7$. Opnieuw is dit geval dus mogelijk. En het geval $n = 8$? Na stug proberen lijkt het telkens maar niet uit te komen en na enige tijd komen we misschien zelfs wel tot het voorzichtige vermoeden dat dit geval, net als de gevallen $n = 2$, $3$, $4$ en $5$, niet kan! De voorwaarde $n \ge 9$ in de opgave lijkt ook te suggereren dat dit het geval zal zijn. Laten we dit geval daarom voor nu even overslaan, maar we zullen er later nog op terugkomen.

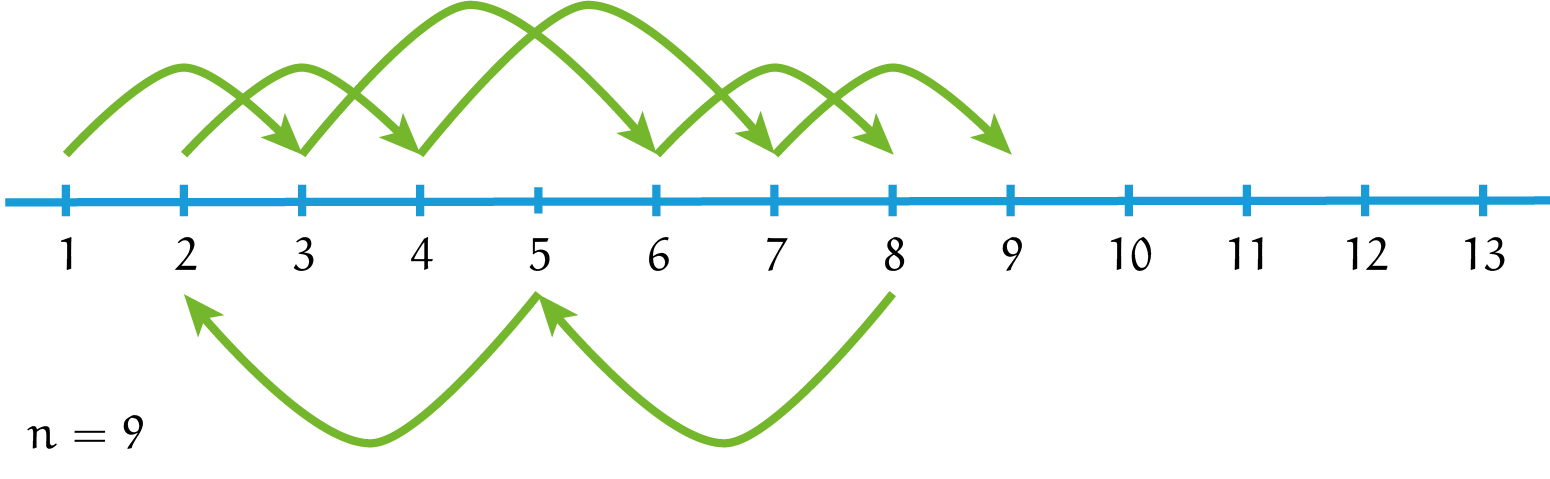
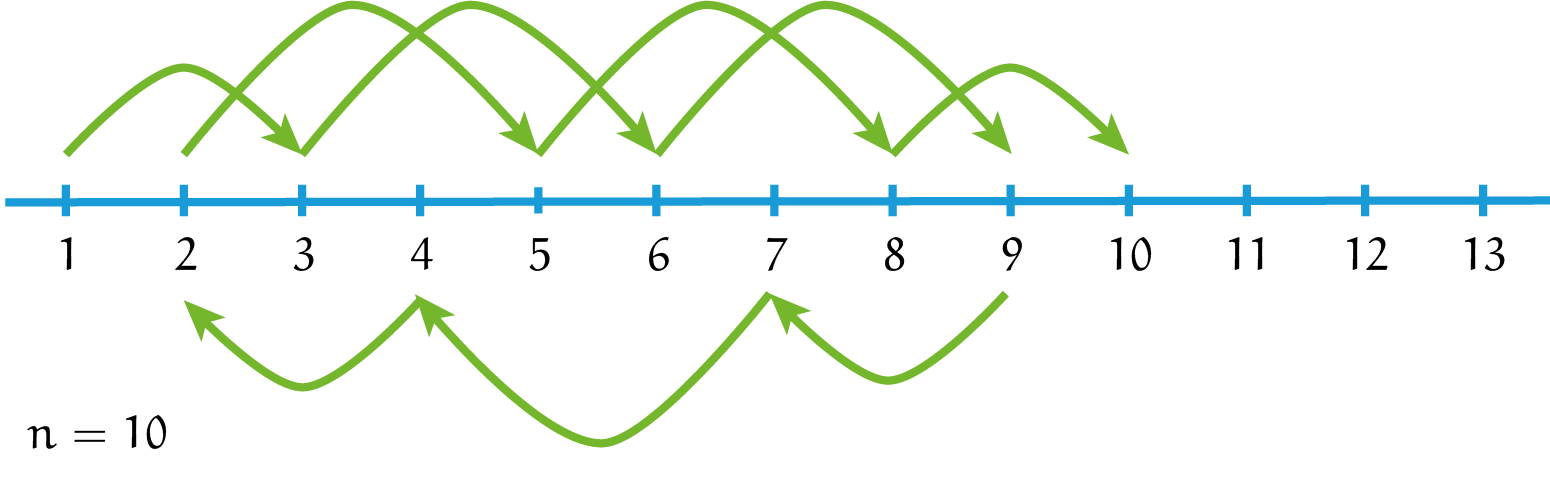
Met inmiddels wat meer gevoel voor het probleem komen we dan eindelijk bij het eerste geval waar de opgave naar vraagt: $n = 9$. Met wat proberen vinden we dan bijvoorbeeld $1-3-6-8-5-2-4-7-9$. Hoe zit het met $n = 10$? Meer proberen levert dan al snel $1-3-6-9-7-4-2-5-8-10$; het ziet er goed uit voor de sprinkhaan!

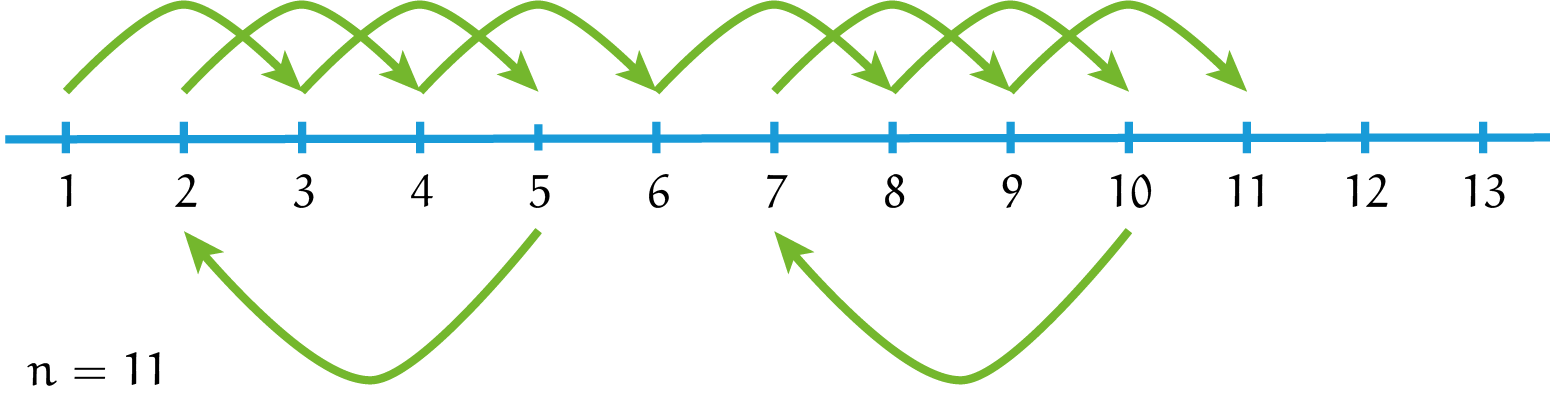
Bij $n = 11$ gebeurt er iets interessants. Als we beginnen met proberen, dan valt ons oog plots op ons eerder gevonden geval voor $n = 6$, namelijk $1-3-5-2-4-6$. De sprinkhaan is nu al bij het getal $6$, dus hoeft hij enkel nog naar $11$ te springen zonder getallen over te slaan. Maar we weten al hoe dit moet! Dit is namelijk precies het probleem voor $n = 6$, maar dan met iets andere getallen. Als we de reeks $6-8-10-7-9-11$ vastplakken aan onze eerdere reeks, vinden we $1-3-5-2-4-6-8-10-7-9-11$.

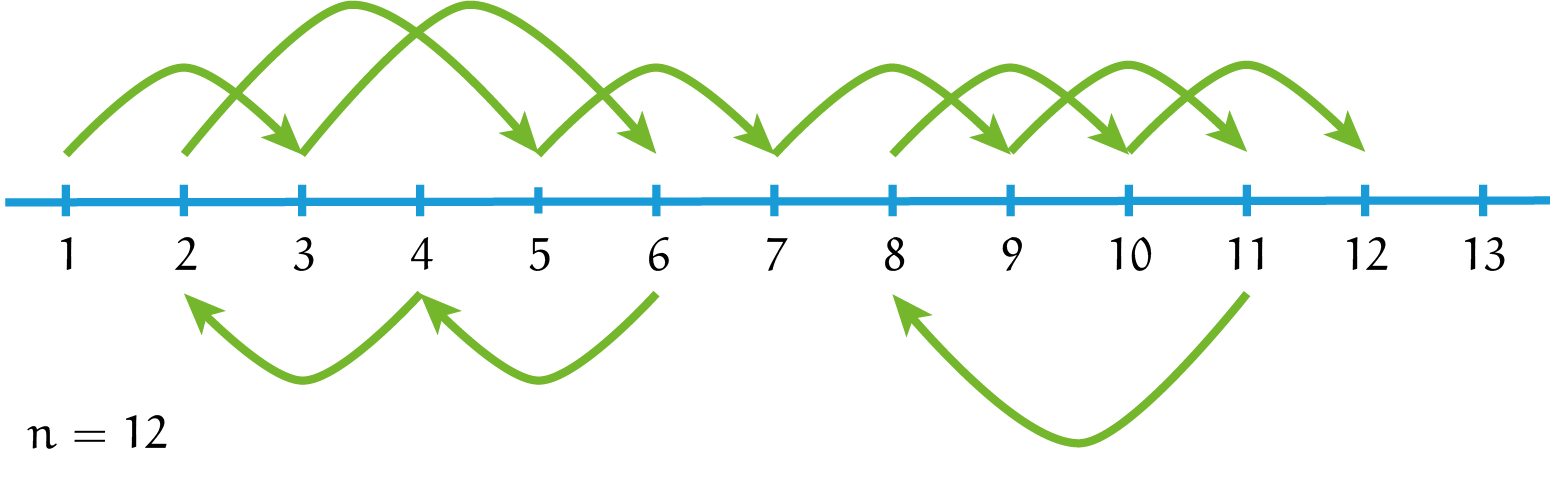
Voor $n = 12$ kunnen we dan iets soortgelijks doen. We kunnen eerst onze oplossing voor $n = 7$ herhalen, en daar dan onze enigszins verschoven oplossing voor $n = 6$ aan vast plakken! Dit levert het rijtje $1-3-6-4-2-5-7-9-11-8-10-12$.

Kunnen we deze strategie in het algemeen toepassen? Stel dat de sprinkhaan een reeks sprongen kan maken van $1$ naar een zeker getal $m$ zonder tussenliggende getallen over te slaan. Door een verschoven versie van onze oplossing voor $n = 6$ hier achter te plakken, vinden we zo altijd een reeks sprongen van de sprinkhaan van $1$ naar $m+5$, opnieuw zonder ook maar iets over te slaan!

Stel dan nu dat we oplossingen hebben voor vijf getallen op een rij; zeg $m$, $m+1$, $m+2$, $m+3$ en $m+4$. Met bovenstaande observatie vinden we dan een oplossing voor $m+5$, en als we hetzelfde idee toepassen op onze oplossing voor $m+1$, $m+2$, $m+3$ en $m+4$, vinden we een oplossing voor $m+6$, $m+7$, $m+8$ en $m+9$. Zo kunnen we doorgaan; onze oplossingen voor $m+5$ tot en met $m+9$ geven weer nieuwe voor $m+10$ tot en met $m+14$, et cetera. Zo vinden we uiteindelijk dus oplossingen voor alle getallen vanaf $m$.

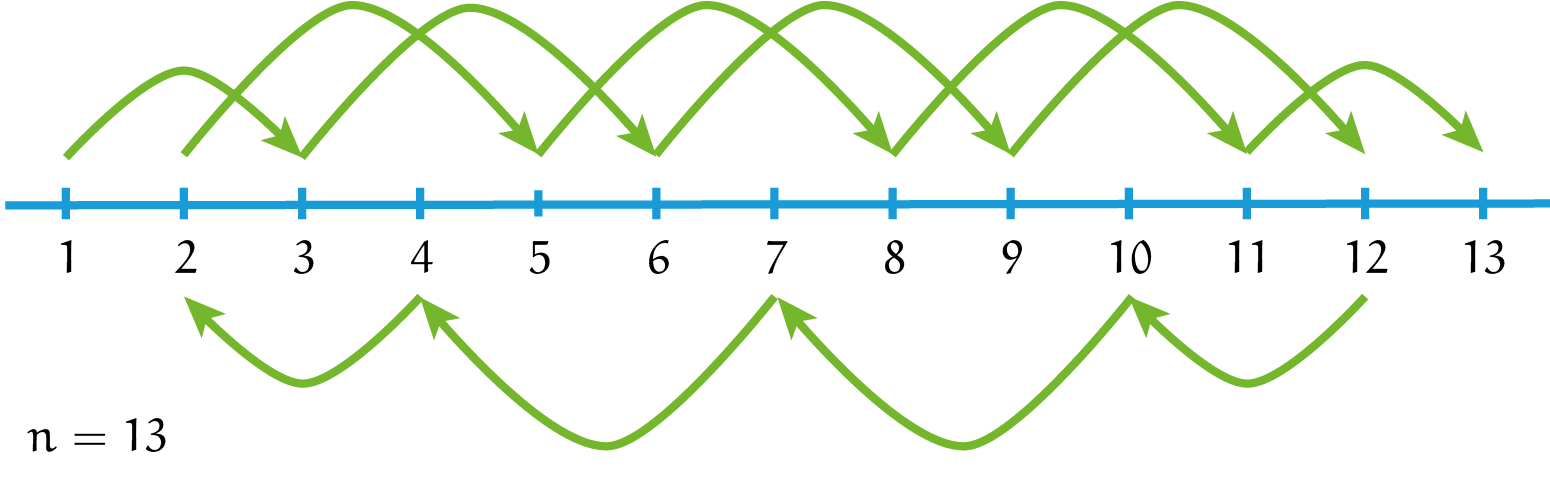
Het volstaat dus om oplossingen te hebben voor $n = 9$, $10$, $11$, $12$ en $13$. De eerste vier hebben we al gedaan, dus resteert nu enkel $n = 13$. Wat proberen levert dat deze inderdaad kan, bijvoorbeeld middels $1-3-6-9-12-10-7-4-2-5-8-11-13$. Zo hebben we de opgave opgelost!

Toch leiden er vaak meerdere wegen naar Rome. Het zou je misschien opgevallen kunnen zijn dat er een soort patroon lijkt te zitten in onze oplossingen voor $n = 9$, $10$ en $13$. Eerst gaan we van $1$ naar $3$ en dan in sprongen van $3$ richting het einde. Dan doen we een sprong van $2$, alvorens met sprongen van $3$ terug te gaan naar $4$ of $2$. Na nog een sprong van $2$ springen we zo met sprongen van $3$ weer terug richting het einde om na een laatste sprong van $2$ ten slotte precies op $n$ uit te komen. Werkt dit ook altijd?

Het begin is altijd hetzelfde; we springen van $1$ naar $3$, en dan via alle drievouden richting $n$. We weten alleen niet precies waar we dan eindigen; dit kan op $n-3$, $n-2$ of $n-1$ zijn, afhankelijk van of $n$ een drievoud plus $3$, $2$ of $1$ is. We moeten dus drie gevallen onderscheiden.

Als we op $n-3$ geland zijn (en $n$ dus een drievoud is), dan springen we eerst nog $2$ naar voren naar $n-1$, zodat we uitkomen op een drievoud plus $2$. Als we dan terugspringen met stappen van $3$, blijven we op drievouden plus $2$ landen, tot we uiteindelijk bij $2$ uitkomen. We springen dan naar $4$, een drievoud plus $1$, en dan vooruit met sprongen van $3$ tot we uitkomen op $n-2$. Dan kunnen we naar $n$; klaar! Omdat we zo langs alle drievouden, alle drievouden plus $1$ en alle drievouden plus $2$ gekomen zijn, moeten we alle getallen wel gehad hebben, dus deze strategie werkt altijd.

Als we op $n-1$ landden ($n$ is nu een drievoud plus $1$), dan springen we juist eerst naar $n-3$; dit is dan een drievoud plus $1$. Terugspringen met sprongen van $3$ brengt ons dan uiteindelijk terug bij $4$. Dan gaan we naar $2$ en met sprongen van $3$ weer vooruit naar $n-2$. Dan kunnen we netjes eindigen op $n$.

In het laatste geval, waarin $n-2$ een drievoud is, werkt een vergelijkbare strategie niet direct; voor $n = 11$ zou je $1-3-6-9-7-4-2-5-8-11$ krijgen, maar dan is het getal $10$ niet bezocht. Stellen we echter even $m = n-5$, dan is $m$ een drievoud, dus kunnen we middels de eerste strategie alle getallen van $1$ tot en met $m$ bezoeken. We sluiten dan af met een verschoven oplossing voor $n = 6$, om zo alle getallen tot en met $n$ te bezoeken. Dit alles samennemend hebben we de opgave nu ook op een heel andere manier opgelost!

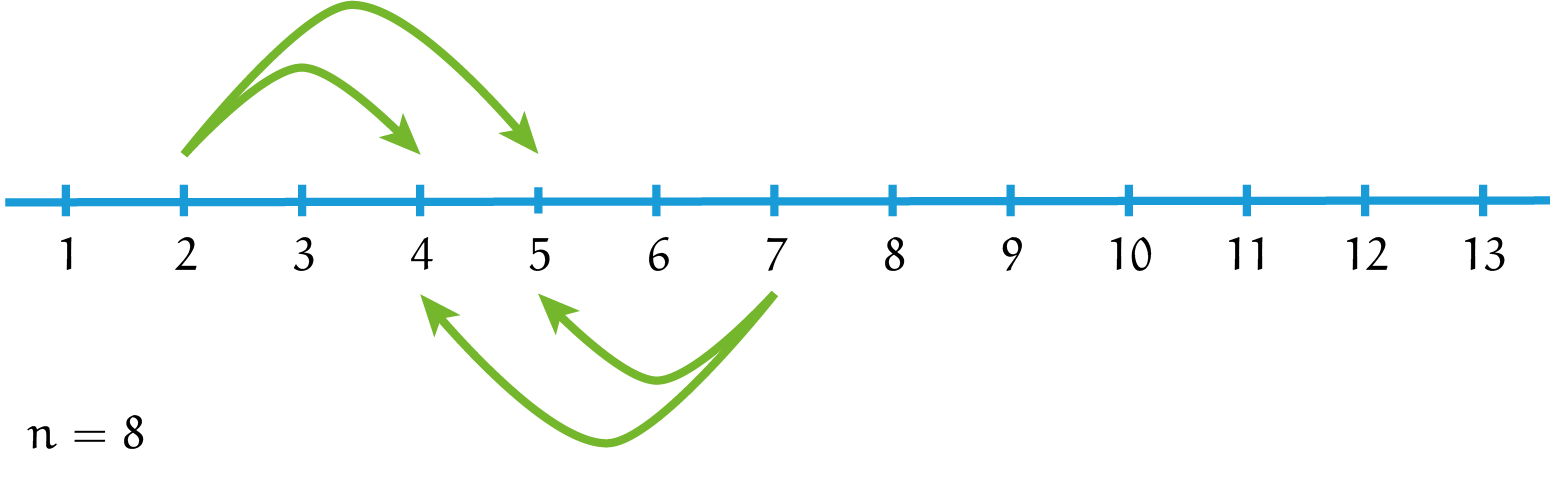
En hoe zit het nu met het geval $n = 8$? Dit leek onmogelijk, maar waarom zou dat zo zijn? Beschouw eens het getal $2$. Vanaf hier kan de sprinkhaan enkel van en naar de getallen $4$ en $5$ springen, en dit geldt hier ook voor het getal $7$. Maar dat is een probleem! Stel dat de sprinkhaan nog bij zowel $2$ als $7$ moet langskomen. Hiervoor moet hij eerst naar $4$ of $5$. Als hij dan naar $2$ gaat en weer terug naar $5$ of $4$, dan moet hij wel naar $7$, maar dan kan hij niet meer terug, want hij is op zowel $4$ als $5$ al geweest! De sprinkhaan kan dus onmogelijk zowel $2$ als $7$ bezoeken; het geval $n = 8$ kan dus niet, en zo weten we nu dus precies voor welke waarden van $n$ de tocht van de sprinkhaan wel mogelijk is, en wanneer dat niet zo is. Dat is zelfs nog meer dan de opgave van ons vroeg!

We hebben nu dus twee verschillende manieren gezien om deze opgave aan te pakken, en beide ideeën kwamen voort uit het doen van veel kleine gevalletjes en het zoeken naar patronen en slimme observaties om ons leven wat makkelijker te maken. Dit zijn belangrijke technieken om in het achterhoofd te houden bij dit soort olympiadesommen, dus onthoud ze goed! Wie weet heb jij dan de volgende keer zo'n lastige C-opgave binnen een mum van tijd opgelost!