De toevalsfactor in priemgetallen
Priemgetallen liggen onregelmatig verdeeld tussen de overige (uit priemgetallen samengestelde) getallen; ze zijn niet in een formule te vangen. Maar als je heel grote getallen bekijkt, kun je wel voorspellingen doen over het aantal en het formaat van de priemfactoren waaruit ze bestaan.
Stel, je neemt een groot, willekeurig getal, en je wilt dit in priemfactoren ontbinden. Is vooraf iets zinnigs te zeggen over het aantal priemfactoren dat dit getal zal hebben? En wat is waarschijnlijker, dat het getal `uiteenvalt' in een heleboel kleine priemfactoren en één grote, of zijn de factoren ongeveer even groot? Sommige dingen liggen voor de hand: de kans dat je getal even is is gelijk aan $\frac12,$ dus de factor $2$ zul je heel vaak tegenkomen. Met iets meer moeite kun je ook wel iets zeggen over het aantal factoren $2$ dat je kunt verwachten. Overigens: vanaf nu schrijven we kortweg ‘factor’ als we ‘priemfactor’ bedoelen; dat scheelt wat tikwerk.
Je kunt zo'n probleem op een paar manieren aanpakken. We doen eerst een experiment. We trekken een steekproef van honderd getallen van achttien cijfers. Ik liet mijn laptop honderd willekeurige getallen van achttien cijfers kiezen (negen getallen begonnen met $0,$ één getal met $00$), en de factoren bepalen. De factoren werden geteld en van elke factor werd ook het aantal cijfers bepaald.
Zo is bijvoorbeeld $709.600.529.873.993.215$ gelijk aan $5 \times 46.993 \times 1.584.169 \times 1.906.379$ dus dit getal heeft één factor van één cijfer, één van vijf cijfers, en twee factoren van zeven cijfers, vier factoren in totaal.
Al dat telwerk leverde deze twee grafieken op.
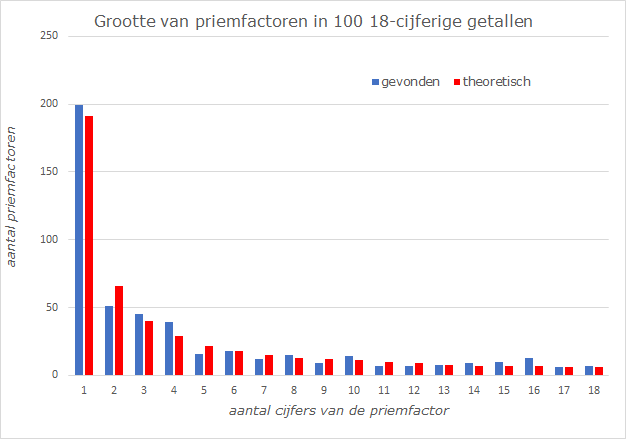
Grafiek 1 |
De aantallen priemfactoren met $1, 2, 3, \dots$ cijfers. In rood de theoretisch verwachte waarden die hieronder uitgerekend worden. |
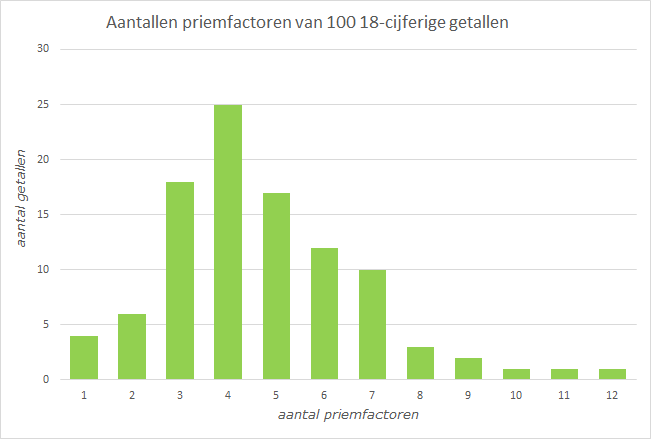
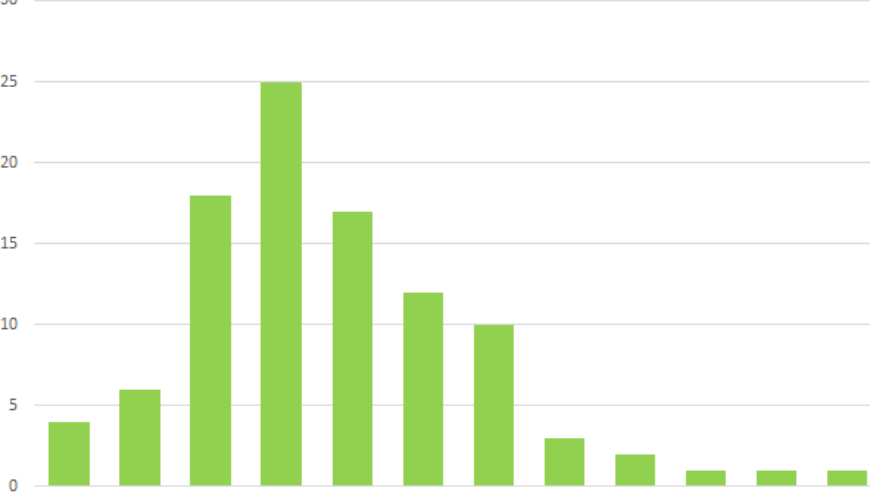
Grafiek 2 |
De aantallen priemfactoren van honderd willekeurige getallen van $18$ cijfers. |
Opgave 1
Voor wie de Pythonlessen volgt: programmeer dit zelf. Schrijf een programma dat $M$ willekeurige getallen van $N$ cijfers kiest, die getallen factoriseert en de bovengenoemde tellingen uitvoert.
Laat het programma ook grafieken als hierboven maken.
Opgave 2
Als je een werkend programma hebt en honderd getallen van achttien cijfers hebt laten verwerken kun je waarschijnlijk wel schatten hoe lang het zou duren om alle getallen van achttien cijfers langs te lopen. Hoe lang heeft jouw computer nodig?
Schattingen
Aannemend dat dit een representatieve steekproef was uit de getallen van achttien cijfers, zijn deze resultaten dan ook theoretisch te verklaren?
Stel je een getallenlijn voor, waarop alle 18-cijfergetallen liggen, van $0$ (dus eigenlijk $000.000.000.000.000.000$) tot $999.999.999.999.999.999$. Onze steekproef is tot stand gekomen door honderd keer ergens op die lijn willekeurig een getal aan te prikken. We bekijken nu hoe de priemgetallen over de getallenlijn verdeeld liggen, waarbij we natuurlijk beginnen met het kleinste priemgetal 2.
We maken een tabel, met boven de getallenlijn genoteerd hoeveel factoren $2$ elk getal bevat. Alle andere factoren negeren we:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
…
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
2
|
…
|
|
|
|
|
2
|
|
|
|
2
|
|
|
|
2
|
|
|
|
2
|
…
|
|
|
2
|
|
2
|
|
2
|
|
2
|
|
2
|
|
2
|
|
2
|
|
2
|
…
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
De oneven getallen hebben geen factor $2$, alle even getallen hebben één of meer factoren $2.$ Je ziet van links naar rechts de ‘torentjes’ van factoren twee steeds hoger worden. Het grootste aantal factoren $2$ dat een 18-cijfer getal kan hebben is $59,$ want $2^{59} = 5{,}76 \times 10^{17}$, iets meer dan de helft van $999.999.999.999.999.999$.
Lagen tweetjes
Als je alleen dit stukje van de getallenlijn bekijkt, kun je gewoon tellen dat de eerste $16$ getallen samen $15$ factoren $2$ hebben, dus gemiddeld heeft een getal op dit lijnstuk $15/16 \approx 0{,}94$ factoren $2$. Wat is het gemiddelde voor een heel lang lijnstuk?
Dat is makkelijker dan het lijkt: de onderste laag tweetjes in de tabel zorgt voor gemiddeld een halve factor $2$, de laag daarboven voor een kwart factor $2$, de derde laag voor een achtste, enzovoort. Gemiddeld zal een getal dus
$$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots$$
factoren $2$ hebben. Waar die som ophoudt, hangt van de lengte van het lijnstuk af; als we doorgaan tot $999.999.999.999.999.999$, dan is de laatste term gelijk aan $2^{-59}$. Wie wel eens een meetkundige rij heeft gezien weet dat de som dat gelijk is aan
$$1-\frac{1}{2^{59}}$$
Opgave 3
Voor wie dit nog niet gezien heeft: noem die som eens $S$ en bekijk wat er gebeurt als je de hele som eerste met $2$ vermenigvuldigt en dan de som zelf daarvan aftrekt. Als dat er te lastig uitziet probeer het dan eerst eens met
$2\times(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16})$ en $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}$.
Maar die som is dus bijna gelijk aan $1$; we doen voor het gemak of hij gelijk is aan $1$. We noteren ons resultaat als $t_2$, dus $t_2=1$. De eerste conclusie is dus als je willekeurige een groot getal pakt is het verwachte aantal factoren $2$ gelijk aan $1$.
Hoe zit het met de factoren $3$?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
…
|
|
|
|
3
|
|
|
3
|
|
|
3
|
|
|
3
|
|
|
3
|
|
…
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Die zijn een stuk dunner gezaaid (pas bij $27$ komen we op de derde laag). De berekening gaat hetzelfde: de eerste laag geeft nu $\frac13$, de tweede geeft $\frac19$, de $k$-de laag geeft dus $3^{-k}$. Omdat $3^{37} = 450.283.905.890.997.363$ stopt onze som bij $3^{-37}$. Met dezelfde methode als eerst kun je uitrekenen dat de som gelijk is aan
$$\frac{1}{2}\left(1-\frac{1}{3^{37}}\right)$$
(reken nu $3^S-S$ uit). Dit scheelt maar weinig van $\frac12$; we concluderen dat de verwachting van het aantal factoren $3$ in een groot willekeurig getal gelijk is aan $t_3=\frac12$.
Dezelfde berekening werkt voor elk priemgetal $p.$ De onderste laag geeft $\frac{1}{p}$, de tweede geeft $\frac{1}{p^2}$, enzovoort. De som wordt nu gelijk aan
$$\frac{1}{p-1}\left(1-\frac{1}{p^k}\right)$$
waarbij $k$ dus zo is dat $p^k\le 10^{18} < p^{k+1}.$
De algemene conclusie is dat voor grote willekeurige getallen het verwachte aantal factoren $p$ gelijk is aan $t_p=\frac{1}{p-1}$.
In ons geval, waar we niet verder gaan dan $10^{18}$ kunnen we nu een schatting maken van het verwachte aantal factoren van een getal van $18$ cijfers:
| $t_2+t_3+t_5+t_7+\dots+t_p$ | ($*$) |
waarbij $p$ het grootste priemgetal onder $10^{18}$ is.
Opgave 4
Voor de Pythonprogrammeurs: schrijf een programma dat dat laatste priemgetal vóór $10^{18}$ bepaalt.
Nu laat de wiskunde het een beetje afweten. Er is geen mooie korte formule voor ($*$), zoals we wel hadden bij de meetkundige rijtjes. Er is nog een verschil: bij de meetkundige rijtjes was er een bovengrens aan de sommen en we zaten al heel dicht bij die grens. Daarom namen we die grens als onze verwachtingswaarde. Bij de som ($*$) is zo'n grens er niet: ook al worden de breuken $\frac{1}{p-1}$ steeds kleiner, de som blijft doorgroeien. Voor elk positief getal $M$ (hoe groot ook) is er een priemgetal $q$ zó dat
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{10}+\cdots+\frac{1}{q-1} > M.$$
Het bewijs, van de wiskundige Leonhard Euler, is niet makkelijk maar met wat volhouden wel te volgen; we komen er nog wel eens op terug in Pythagoras.
We vergelijken wat deelresultaten met onze steekproef. Met een eenvoudig rekenmachientje (of zelfs met de hand) is het verwachte aantal factoren met één cijfer snel bepaald:
$$E_1=t_2+t_3+t_5+t_7=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{6}=\frac{23}{12}\approx1{,}9167.$$
Volgens de eerste grafiek is het gemiddelde voor onze steekproef gelijk aan $199/100 = 1{,}99$. Dat klopt redelijk.
Voor factoren met twee cijfers is het meer werk:
$$E_2=t_{11}+\cdots+t_{97}=\frac{1}{10}+\cdots+\frac{1}{96}\approx0{,}6575.$$
Volgens de eerste grafiek heeft onze steekproef gemiddeld $51/100 = 0{,}51$ factoren van twee cijfers.
En voor drie cijfers krijgen we $143$ termen:
$$E_3=t_{101}+\cdots+t_{997}=\frac{1}{100}+\cdots+\frac{1}{996} ≈ 0{,}397.$$
In de steekproef hebben we gemiddeld $45/100 = 0{,}45$ factoren van drie cijfers.
Als we die aantallen bij elkaar optellen komen we in de steekproef op gemiddeld $1{,}99 + 0{,}51 + 0{,}45 = 2{,}95$ factoren met ten hoogste drie cijfers. De theorie komt op $E_1 + E_2 + E_3 = 2{,}97$. Voor een steekproef van honderd uit $10^{18}$ is dat best goed.
Het met de hand-en-rekenmachine bepalen van $E_4$ is al een heel werk want er zijn $1061$ priemgetallen van vier cijfers. Voor $E_5$ en verder kunnen we niet zonder de computer. Daarom laten we het hier nu bij. In een volgend artikel laten we zien hoe je op een statistische manier, maar zonder computer, toch iets kunt zeggen over het gemiddeld aantal factoren van een groot getal $N$.
Opgave 5
Schrijf een programma dat $E_4, E_5$ en $E_6$ berekent. Laat Python de tijd bijhouden. Bij welk aantal cijfers gaat het te lang duren?
