Een leuke variant op het trekken van ballen uit een vaas is het trekken uit een vaas van Pólya. György Pólya was een Hongaarse wiskundige die leefde van 1878 tot 1985. Pólya was een man met vele interesses. Hij studeerde eerst rechten, daarna literatuur en filosofie, maar uiteindelijk kwam hij uit bij de wiskunde. Naar eigen zeggen raakte hij geïnteresseerd in de wiskunde door een wiskundeblad voor middelbare scholieren, de Középiskolai Matematikai Lapok. Een Hongaarse versie van Pythagoras dus, en het is daarom logisch dat er in dit blad aandacht wordt besteed aan György Pólya en de naar hem genoemde vaas.

Laten we beginnen met een simpel voorbeeld. We hebben een vaas met 8 rode en 5 zwarte ballen.

Trekken zonder teruglegging

We nemen twee keer een bal uit deze vaas en leggen de bal daarna niet terug meer in de vaas. Dit is dus het normale trekken zonder teruglegging.

 

Opgave 1 Wat is de kans dat er na twee keer trekken nog $7$ rode ballen in de vaas overblijven?   Antwoord Als er na twee keer trekken nog 7 rode ballen overgebleven zijn betekent dat dat er één keer een rode bal is getrokken. Dat kan op twee manieren: eerst rood, dan zwart (RZ) of eerst zwart, dan rood (ZR).  De kans op RZ wordt gegeven door  $P({\rm RZ}) = \frac{8}{13}\cdot \frac{5}{12}$. De kans $P({\rm ZR})$ is even groot (de tellers van de breuken kun je immers van plaats verwisselen zonder dat het product van de twee breuken verandert). De totale kans op 7 ballen na twee keer trekken is de som van beide kansen, dus  $P(7$ rood na twee keer trekken$) = 2\cdot\frac{8}{13}\cdot\frac{5}{12}\approx 0{,}513$.

 Voor grotere getallen is de afleiding gelijk, maar het is dan beter om systematischer te werk te gaan, zoals het volgende voorbeeld laat zien.

Opgave 2 Wat is de kans dat we na vier keer trekken nog $6$ rode ballen hebben?   Antwoord Na vier keer trekken nog $6$ rode ballen betekent dat er twee keer een rode bal is getrokken en de twee andere keer een zwarte bal. Op hoeveel verschillende manieren kan dat? Een vergelijkbare situatie is dat je een aantal letters hebt, en met die letters probeer je woorden te vormen. Stel je voor dat je de letters R, R, Z en Z hebt. Hoeveel verschillende "woorden" van 4 letters kun je daarmee maken als je elke letter maar één keer mag gebruiken? Na enig nadenken is in te zien dat je voor de eerste letter van het woord kan kiezen uit 4 letters. Voor de tweede letter kun je kiezen uit de drie overgebleven letters, Voor de derde letter kun je kiezen uit de twee letters die dan nog over zijn en voor de laatste letter gebruik je dan de laatst overgebleven letter. Dat zou betekenen dat je $4 \cdot 3 \cdot 2 \cdot 1 = 4! = 24$ woorden kan vormen. Maar pas op! Omdat je twee keer de letter R en twee keer de letter Z hebt zijn sommige van die $24$ woorden gelijk. Het juiste aantal verschillende woorden krijg je door het totale aantal $24$ te delen door het aantal $R!$ ($R$ is het aantal letters "R" dat we hebben, $2$ in dit voorbeeld) en het getal wat je dan krijgt nog een keer te delen door $Z!$ ($Z$ is het aantal letters "Z" dat we hebben, $2$ in dit voorbeeld). Terugvertalend naar ons probleem betekent dat dus dat je op $\frac{4!}{2!2!}=6$ manieren twee rode ballen kan trekken als je vier keer een bal trekt. Volledig uitgeschreven is dat op de volgende manieren: RRZZ  RZRZ  RZZR  ZZRR  ZRZR  ZRRZ De kans op elk van die 6 keer is weer gelijk. Nemen we bijvoorbeeld de kans op de reeks RRZZ, dan is die kans gelijk aan $P({\rm RRZZ})=\frac{8}{13}\cdot\frac{7}{12}\cdot\frac{5}{11}\cdot\frac{4}{10}$. De totale kans op 6 rode ballen op het eind is dan $P($6 rood na 4 keer trekken$)=\frac{4!}{2!2!}\cdot\frac{8}{13}\cdot\frac{7}{12}\cdot\frac{5}{11}\cdot\frac{4}{10}\approx 0{,}392$.

Teruglegging volgens Pólya 

Een andere mogelijkheid is dat we na de eerste trekking de bal weer terugleggen, samen met nóg een bal van dezelfde kleur. Dus als we bij de eerste trekking bijvoorbeeld een zwarte bal trekken, leggen we twee zwarte ballen terug in de vaas, en als we een rode bal trekken leggen we twee rode ballen terug. Dit is het principe van de vaas van Pólya. Dit is feitelijk het tegenovergestelde van trekken zonder teruglegging.

Een eerste verschil met trekken zonder terugleggen is dat met deze manier het aantal ballen van een kleur nooit minder kan worden, alleen maar meer. We kunnen dus eindeloos blijven trekken uit deze vaas. Het wordt dan interessant om te kijken wat er gebeurt als je bv. 100 keer een bal trekt uit een vaas met een klein aantal ballen ($\ll 100$ : veel kleiner dan $100$).

Laten we weer uitgaan van een vaas met $8$ rode en $5$ zwarte ballen.

Opgave 3 Wat is de kans dat we na twee keer trekken precies $9$ rode ballen in de vaas hebben?   Antwoord Op welke manieren kunnen we na twee keer trekken $9$ rode ballen hebben? Dat kan als we het volgende doen:eerst rood, dan zwart (RZ) of eerst zwart, dan rood (ZR). Deze kans P(RZ) wordt gegeven door $P({\rm RZ}) = \frac{8}{13}\cdot\frac{5}{14}$. Zoals we zien is deze kans ook weer gelijk aan $P({\rm ZR})$. De totale kans op $9$ rood na twee keer een bal trekken is dus $P(9$ rood na 2 keer trekken$) = 2\cdot\frac{8}{13}\cdot\frac{5}{14}\approx 0{,}440$.

Laten we als laatste oefening nog berekenen hoe groot de kans is op 10 rode ballen na vier keer trekken.

Het is duidelijk dat we van de vier keer dan twee keer rood moeten hebben getrokken. De andere twee keer moet dan zwart zijn. We hebben dus weer de letters RRZZ waar we verschillende "woorden" mee moeten maken. Op dezelfde manier als bij trekken zonder teruglegging vinden we

$P(10$ rood na 4 keer trekken$) =\frac{4!}{2!2!}\cdot\frac{8}{13}\cdot\frac{9}{14}\cdot\frac{5}{15}\cdot\frac{6}{16}\approx 0{,}297$.

Vergeleken met trekken zonder teruglegging zien we dat naarmate er vaker getrokken wordt uit de vaas de verhoudingen tussen rood en zwart na een trekking steeds minder veranderen. Met andere woorden: de verdeling rood en zwart wordt steeds stabieler. Juist in het begin kan de verhouding rood/zwart nog sterk wijzigen, en dat betekent dat bij deze manier van trekken kleine verschillen in het begin sterk uitvergroot worden naarmate we vaker trekken. Dit kan mooi geïllustreerd worden met een online simulatietool, te vinden op Pólya Urn Model.

Als we bijvoorbeeld 100 keer trekken kan de verdeling er uit komen te zien als in figuur 1.

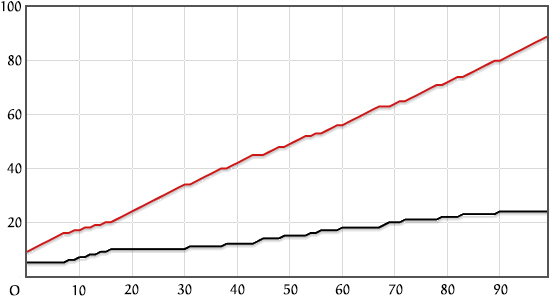
Als je meerdere keren deze simulatie draait zul je dit vaak zien. Aangezien er in het begin al meer rode dan zwarte ballen zijn, is de eerste keer de kans op rood groter dan op zwart. En na het trekken van rood zal de kans op rood alleen maar groter worden. Na honderd keer trekken zullen er in de vaas $8 + 5 + 100 = 113$ ballen zitten waarvan het grootste deel rood.

Toch zal het af en toe ook gebeuren dat toevallig in het begin zwart de overhand krijgt, waarna na $100$ keer trekken zwart in de meerderheid zal zijn. Dat zien we gebeuren in de volgende simulatie in figuur 2.

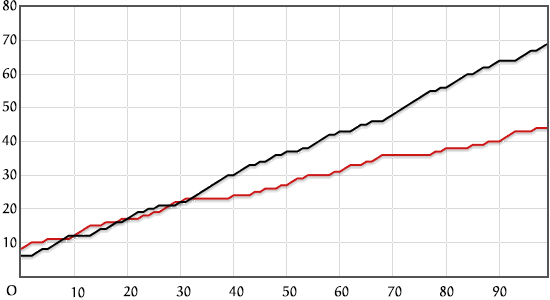
Het is leuk om zelf deze simulaties te doen op de genoemde website.

Het is ook mogelijk om op bovengenoemde website meerdere kleuren in de vaas te hebben. Vul in hoeveel ballen we van elke kleur hebben en kijk wat er gebeurt als je honderd keer uit deze vaas trekt.

De methode van terugleggen bij de vaas van Pólya is te simpel om als model te dienen voor enige realistische situatie. Maar er zijn varianten te bedenken die wel praktische toepassingen kennen. Een manier van terugleggen die er erg op lijkt is bijvoorbeeld het Moranproces. We nemen een bal uit de vaas, leggen hem weer terug samen met nog een bal van dezelfde kleur, net als bij Pólya. Maar daarnaast kiezen we nóg een bal uit de vaas die we definitief verwijderen. Het totale aantal ballen blijft dus constant. Dit kan bijvoorbeeld als model dienen voor een klomp cellen, waarbij een cel zich splitst in tweeën en tegelijkertijd een cel afsterft. Ook uit zo'n vaas kunnen we eindeloos blijven trekken en het is interessant om te zien hoe de inhoud van de vaas zich ontwikkelt. Misschien dat in een volgend artikel hier dieper op kan worden ingegaan.

		Frank Brandse is docent Toegepaste Wiskunde bij Hogeschool InHolland. Bij de opleiding Toegepaste Wiskunde leer je op een wiskundige manier naar vraagstukken te kijken. De wiskundige kennis en vaardigheden die je op de middelbare school hebt geleerd, worden flink uitgebreid. Verder leer je hoe je het aangeleerde kunt toepassen in verschillende domeinen zoals de logistiek en techniek. Afhankelijk van de Hogeschool waar je de opleiding volgt is er naast wiskundevakken als calculus en lineaire algebra aandacht voor statistiek, kansberekening, operations research, data science en artificial intelligence. Gedurende de hele opleiding werk je naast de theorievakken aan projecten waarin je het geleerde direct in de praktijk brengt en word je getraind in professionele vaardigheden als presenteren en projectmatig werken. Van de vier jaar die de opleiding duurt loop je ongeveer een jaar stage buiten school. Je kunt de opleiding op vijf HBO's volgen: bij Fontys in Eindhoven, de Haagse Hogeschool in Delft, bij de Hogeschool van Amsterdam en InHolland in Amsterdam en bij NHL Stenden in Leeuwarden.