Bij darts gooi je om de beurt drie pijlen op een dartbord. In figuur 1 kun je zien hoe een dartbord eruit ziet en hoeveel punten je krijgt afhankelijk van waar je gooit. Een dartbord bestaat uit 20 delen, en een enkele en dubbele Bullseye. De dubbele of binnenste Bullseye is 50 punten waard, de enkele 25. Voor de zwarte en witte vakjes geldt dat je de score tussen 1 en 20 krijgt. De buitenste gekleurde ring verdubbelt het aantal punten, de binnenste gekleurde ring verdriedubbelt het aantal punten. Je krijgt dus de meeste punten als je de triple 20 raakt. Topdarters zoals Michael van Gerwen en Raymond van Barneveld mikken daar bijna altijd op.

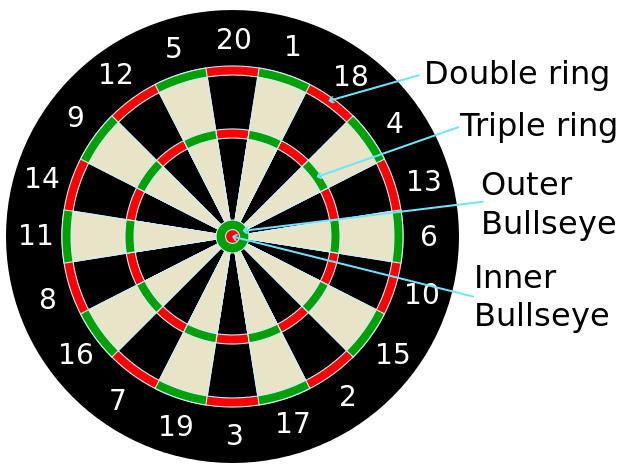
Figuur 1a: Een dartbord

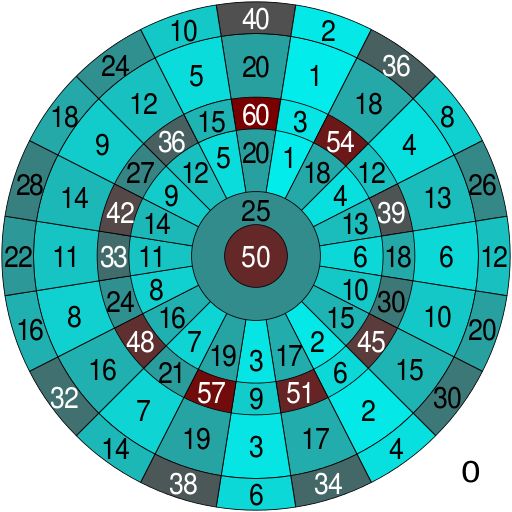
Figuur 1b: De score die je krijgt afhankelijk van waar je gooit

Het doel bij darts is om zo snel mogelijk een score van 501 te halen, dan heb je één leg gewonnen. Je moet altijd eindigen met een pijl in de buitenste ring, een “dubbel”. In theorie is het mogelijk om in 9 darts uit te gooien, maar dat gebeurt bijna nooit. Op televisie is dat sinds 1984 51 keer voorgekomen. Je kunt een 9-darter gooien door bijvoorbeeld zeven keer triple 20 te gooien, één keer triple 19, en te eindigen met dubbel 12.

Opgave

Kun je nog een manier verzinnen om met 9 darts 501 te gooien? Hoeveel mogelijkheden zijn er in totaal?

(Zie nl.wikipedia.org/wiki/9-darter)

Stel nu dat je de eerste pijl gooit. Je wil een naar verwachting zo hoog mogelijke score gooien. Waar moet je dan mikken? Ryan Tibshirani, Andrew Price en Jonathan Taylor van de universiteit van Stanford zochten dat uit in hun artikel A statistician plays darts. Dit hangt af van hoe nauwkeurig je kunt gooien. In eerste instantie gaan ze er vanuit dat je mikt op een plek $\mu$ met coördinaten $\mu_x$ en $\mu_y$. Ze nemen aan dat de afwijking in de $x$-richting en $y$-richting normaal verdeeld is met een gemiddelde van $0$ en een standaardafwijking $\sigma$. De verwachte score hangt af van $\mu$ (waar je mikt) en $\sigma$ (hoe nauwkeurig je kunt gooien). Ze berekenden de verwachte score voor drie standaarddeviaties: $5$ mm, $26{,}9$ mm en $64{,}6$ mm. De laatste twee standaarddeviaties zijn inschattingen van de nauwkeurigheid van twee van de schrijvers van het artikel. Een standaarddeviatie van $5$ mm is heel nauwkeurig. In figuur 2 is een simulatie te zien van 30 pijlen van iemand die mikt op het midden van de triple 20 ($\mu_x = 0$ mm, $\mu_y = 103$ mm) met een standaarddeviatie van $26{,}9$ mm.

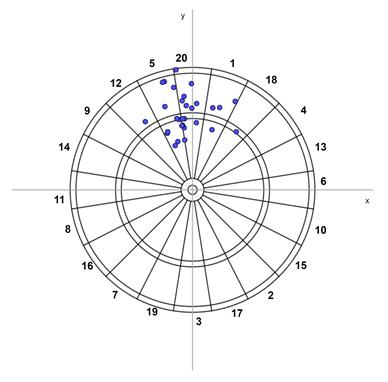
Figuur 2: Simulatie van 30 pijlen

Een dartbord heeft een straal van $170$ mm, de straal van de binnenste Bullseye is $6{,}35$ mm. Stel dat een darter met een standaarddeviatie van $5$ mm op het midden van het bord mikt. De kans dat hij de binnenste Bullseye raakt is dan ruim $55\%$. Daar zou Michael van Gerwen best tevreden mee zijn!

Op basis van deze aannames hebben de auteurs voor elk punt op het dartbord berekend wat de verwachte score is als een darter daar op mikt. Dat hebben ze gedaan door het dartbord op te delen in hele kleine stukjes, bijvoorbeeld van een vierkante millimeter. Voor elk van die vakjes hebben ze de kans dat de pijl in dat vakje terecht komt benaderd, vermenigvuldigd met de score in dat vakje, en al die waardes bij elkaar opgeteld. Het resultaat is te zien in figuur 3. Voor de drie standaarddeviaties is met een kleur aangegeven wat de verwachte score is afhankelijk van de plek waar de darter op mikt. We noemen dit ook wel een heatmap. Een lichtere kleur geeft een hogere verwachte score aan. De balk links in de figuur geeft aan welke kleur met welke verwachte score overeenkomt. De kleurschaal verschilt in de drie situaties.

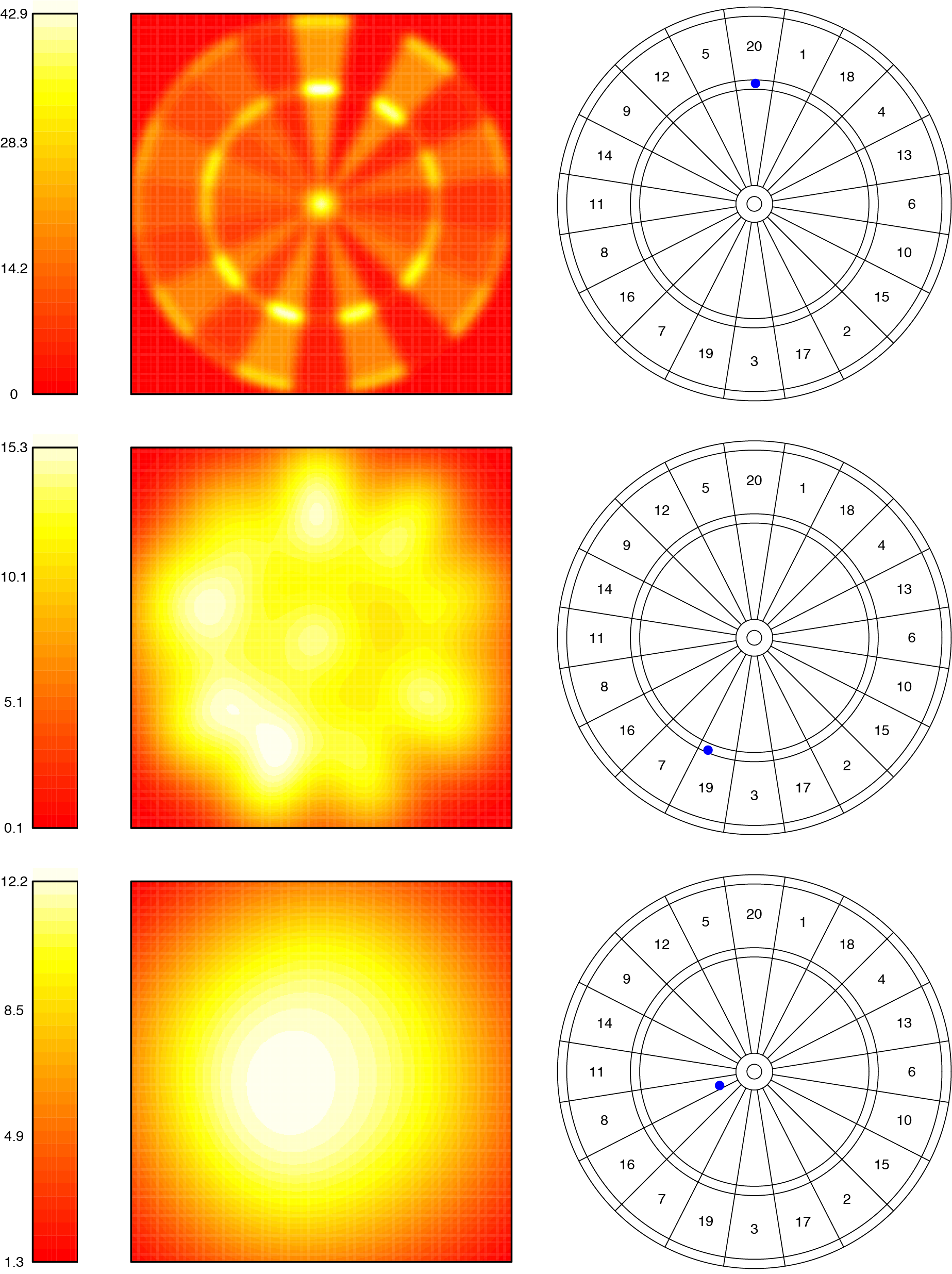
Figuur 3: Links: Heatmap van verwachte score van één pijl bij een standaarddeviatie van 5mm (a), 26,9 mm (b) en 64,6 mm (C). Een lichtere kleur geeft een hogere verwachte score aan. Rechts: Plek met de hoogste verwachte score.

Bij een standaarddeviatie van $5$ mm ligt de verwachte score per pijl tussen de $0$ en $42,9$. De triple 20 geeft de hoogste verwachte score. Voor 3 pijlen komt dat neer op een verwachte score van bijna $129$. Topspelers halen zelden een gemiddelde boven de $120$. Dat is geen hele eerlijke vergelijking, want spelers mikken niet altijd op de triple 20, maar het geeft wel aan dat een standaarddeviatie van $5$ mm een soort ondergrens is. De maximale verwachte score bij een standaarddeviatie van $26{,}9$ mm ligt een stuk lager. De optimale plek om te mikken is dan de triple 19, met een verwachte score van $15{,}3$ per pijl. De scores rondom de triple 19 zijn gemiddeld hoger dan die om de triple 20. Als je je doel mist haal je toch nog wat meer punten, waardoor de verwachte score hoger is dan wanneer je op de triple 20 mikt. Als je nog onnauwkeuriger gaat gooien kun je het beste iets links onder het midden mikken. Dit is ook wel te begrijpen. Stel dat je heel erg onnauwkeurig gooit, zo erg dat je moeite hebt om het bord te raken. Dan kun je het beste in het midden mikken, omdat de kans dan het grootst is dat je het bord raakt. In figuur 4 is voor alle standaarddeviaties tussen $0$ en $100$ mm te zien wat de optimale plek is om op te mikken.

Figuur 4: Plek met de hoogste verwachte score afhankelijk van de standaarddeviatie tussen 0 en 100mm. De optimale plek start in de triple 20 bij σ = 0, springt bij σ =16,4 naar de triple 19, en gaat dan richting de Bullseye.

Tot nu toe namen we aan dat de afwijkingen in de $x$-richting en de $y$-richting normaal verdeeld zijn met dezelfde standaarddeviatie. Alleen de afstand tot het mikpunt $\mu$ is belangrijk. Als je dat aanneemt komen afwijkingen in alle vier de kwadranten, linksboven, linksonder, rechtsboven en rechtsonder $\mu$, gemiddeld genomen even vaak voor. In de praktijk blijkt dit vaak net wat anders te liggen. De meeste spelers hebben een grotere afwijking in de $y$-richting dan in de $x$-richting. Ook komt de pijl van rechtshandige spelers vaker linksboven en rechtsonder het doel terecht dan linksonder en rechtsboven. Een voorbeeld van zo’n patroon is te zien in figuur 5. Bij andere verdelingen kun je nog steeds dezelfde methode gebruiken om de verwachte score te berekenen. De heatmaps uit figuur 3 veranderen dan een beetje, maar de conclusies blijven ongeveer hetzelfde. Het is bijna nooit voordelig om op de triple 20 te richten. En als je heel onnauwkeurig gooit, kun je het beste op de Bullseye mikken. Wellicht kun je deze informatie gebruiken als je zelf eens een potje darts speelt!

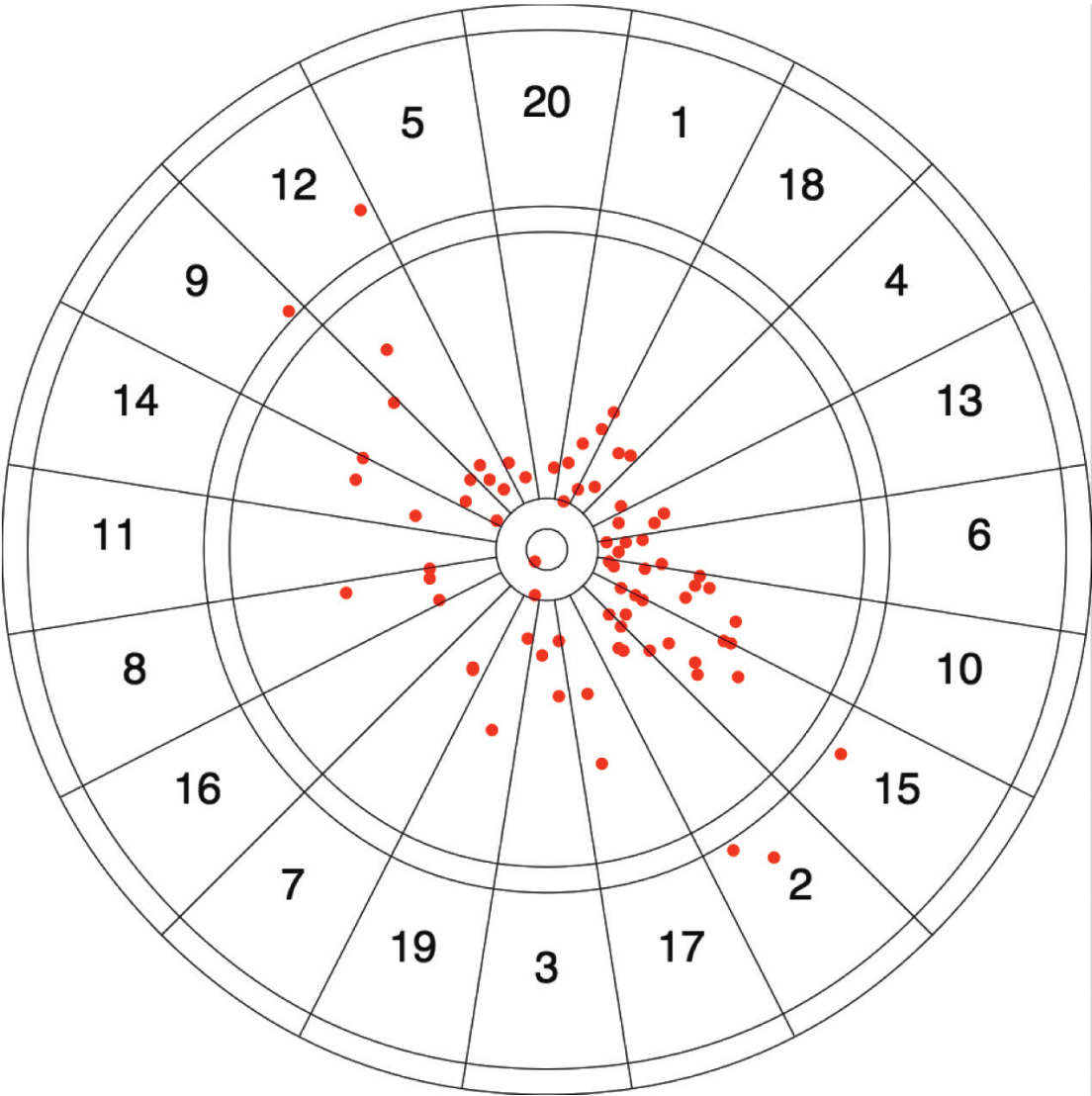
Figuur 5: Darts van een typische rechtshandige speler die mikt op de Bullseye. Afwijkingen linksboven en rechtsonder het doel komen vaker voor dan linksonder en rechtsboven. De afwijking in de y-richting is groter dan de afwijking in de x-richting.

 

Bronnen:

Peacock, J., Maxey, J., & Tymms, V. (2015). Left out?. Significance, 12(2), 36-39.

Tibshirani, R. J., Price, A., & Taylor, J. (2011). A statistician plays darts. Journal of the Royal Statistical Society: Series A (Statistics in Society), 174(1), 213-226.