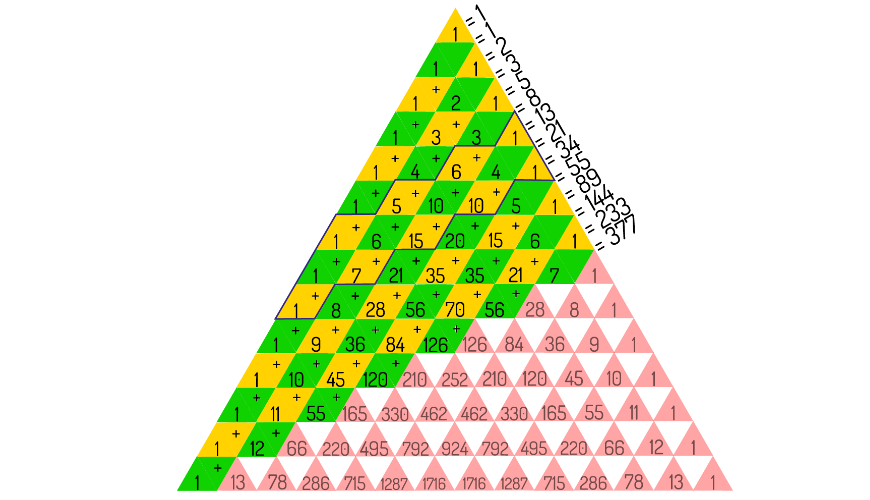
Driehoek van Pascal 57-5/6
De rij getallen 1, 1, 2, 3, 5, 8, 13, 21, … die begint met twee keer 1 en waarvan het volgende getal steeds de som van de twee vorige is, is de bekende getallenrij van Fibonacci. Je vindt die rij terug in de driehoek van Pascal als je de getallen in de driehoek diagonaalsgewijs optelt – de kleuren geven aan hoe.
De verklaring hiervoor wordt gegeven in onderstaand detail:
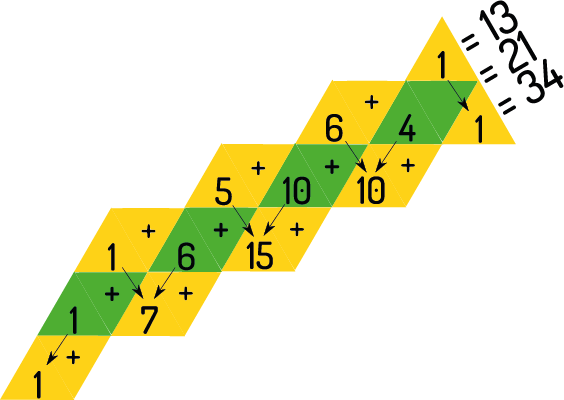
Je ziet dat de som van de getallen op de onderste diagonaal gelijk is aan de som van alle getallen op de twee vorige, een gevolg van de definiërende eigenschap van de driehoek van Pascal: elk element niet op de rand is gelijk aan de som van de twee getallen die erboven staan. Dus de volgende diagonaalsom is gelijk aan de som van de twee vorige, en bovendien zijn de eerste twee beide gelijk aan 1, precies wat je moet hebben voor de rij van Fibonacci.
