De eerste ronde van afgelopen januari bestond zoals elk jaar uit acht meerkeuzevragen, de A-vragen, en vier open vragen, de B-vragen. Normaliter loopt de moeilijkheidsgraad gedurende de toets op, maar dit jaar bleek de een na laatste opgave, opgave B3, het lastigst. Slechts 3% van alle deelnemers wist hier het goede antwoord neer te zetten. Laten we eens zelf voor de opgave gaan zitten en een poging wagen.

Eerste ronde 2022 opgave B3 Op een congres zijn alle aanwezigen wiskundige of bioloog en is er niemand zowel wiskundige als bioloog. De wiskundigen kennen elkaar allemaal en kennen elk vier van de biologen. De biologen kennen elkaar allemaal en kennen elk negen van de wiskundigen. Het blijkt dat elke wiskundige precies twee keer zoveel mensen kent als elke bioloog. (Als persoon A persoon B kent, dan kent persoon B ook persoon A.) Hoeveel wiskundigen zijn er op het congres?

Zoals je ziet krijg je in de eerste regels een flinke hap informatie voorgeschoteld. Pas in de laatste zin wordt het duidelijk dat je het aantal wiskundigen moet uitrekenen. Misschien heeft dat je verrast, omdat je helemaal nog niet de intuïtie had dat dat aantal vastlag. Je zou niet de enige zijn geweest: het is ook helemaal niet eenvoudig om te weten hoe je met zo'n opgave zou beginnen.

Allereerst hebben we een manier nodig om alles over zo’n congres weer te geven. We zouden iedereen op het congres een 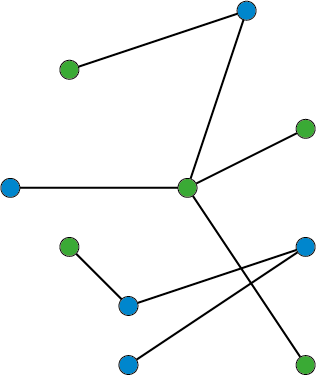naam kunnen geven en per persoon lijstjes kunnen maken met al zijn kennissen, maar dat is duidelijk erg veel werk en bovendien onoverzichtelijk. Een veel betere manier om een congres te visualiseren is een graaf: een aantal punten die al dan niet verbonden zijn door lijnstukken. We zetten voor elke persoon een stip op het papier. Omdat niemand zowel wiskundige als bioloog is, maken we die van de wiskundigen blauw en die van de biologen groen. Als twee mensen elkaar kennen, dan trekken we een lijntje tussen hun stippen. Zo kunnen we alles in een oogopslag zien. 

Dat ziet er al mooi uit, maar hoe nu verder? Hoe komen we erachter wat voor congres aan de eisen voldoet? Het antwoord op die vraag is simpel: gewoon proberen. Als we proberen een graaf te tekenen die aan de eisen voldoet, kunnen er twee dingen gebeuren. Als we geluk hebben, voldoet de graaf. Anders voldoet de graaf niet, maar dat kan ons dan inzicht geven in waarom bepaalde grafen wel of niet voldoen!

Dat is makkelijer gezegd dan gedaan. Hoeveel stipjes moeten we tekenen en hoeveel lijntjes? Dat kun je van tevoren natuurlijk helemaal niet weten. Laten we eens terugkijken naar de opgave. Er staat dat elke wiskundige vier biologen kent en elke bioloog negen wiskundigen. Dat betekent dat er minimaal vier biologen en minimaal negen wiskundigen zijn. Laten we die situatie eens tekenen.

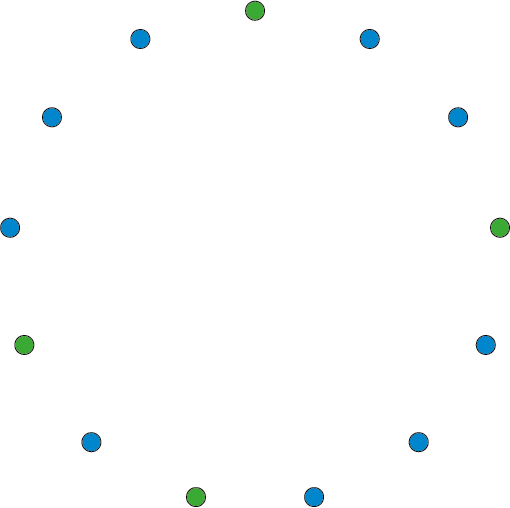
De stipjes waren natuurlijk makkelijk, maar waar moeten we nu de lijntjes trekken? Elke wiskundige kent de vier biologen, maar ook de andere acht wiskundigen. Net zo kent elke bioloog de negen wiskundigen en de overige drie biologen. Kortom, iedereen kent iedereen.

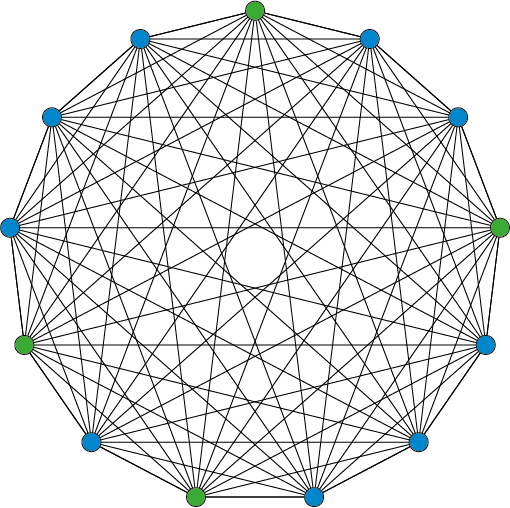
Zijn we dan nu al klaar met de opgave en is het antwoord negen? Nee; hoewel elke wiskundige precies vier biologen kent en elke bioloog precies negen wiskundigen, moeten we nog kijken naar de andere eis: elke wiskundige kent precies twee keer zoveel mensen als elke bioloog. Dit is hier duidelijk niet zo, want iedereen kent precies de andere twaalf mensen.

We merken dat het combineren met die laatste eis nog knap lastig is. Hoe zouden we kunnen garanderen dat elke wiskundige twee keer zoveel mensen kent als elke bioloog? Hiervoor moeten we eerst maar eens tellen hoeveel mensen een bioloog of wiskundige überhaupt kent. Dit aantal hangt natuurlijk af van hoeveel mensen er zijn. Laten we het aantal biologen $b$ noemen en het aantal wiskundigen $w$. Op het congres kent een bioloog alle overige $b - 1$ biologen, plus nog $9$ wiskundigen, dus een bioloog kent $b + 8$ mensen. Een wiskundige kent juist $w - 1$ wiskundigen en $4$ biologen, dus in totaal $w + 3$ mensen. Omdat dat aantal twee keer zo groot moet zijn, zien we dat $w + 3 = 2(b + 8)$, wat we kunnen vereenvoudigen tot $w + 3 = 2b + 16$, dus $w = 2b + 13$.

Die vergelijking is een prachtig inzicht, maar we weten nog niet genoeg. We gaan onze nieuwe informatie gebruiken om een graaf te tekenen die meer kans maakt. Er moeten minimaal vier biologen zijn, dus laten we nemen dat $b = 4$. Dan geldt $w = 21$. Dat is natuurlijk wel een tegenvaller, want bij zo’n enorme graaf wil je eigenlijk helemaal geen lijntjes gaan trekken. In dit geval kunnen we het gelukkig nog slim aanpakken, zonder te tekenen. Omdat elke wiskundige precies vier biologen moet kennen en er nu maar vier zijn, kent elke wiskundige elke bioloog. Dat betekent dat elke bioloog ook precies alle $21$ wiskundigen kent! Dat is veel meer dan de vereiste negen, dus ook dit congres blijkt niet te voldoen.

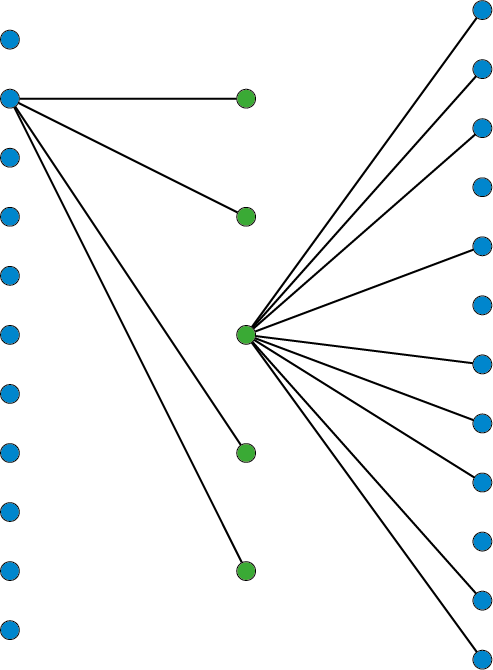Nu we weten dat er moet gelden dat $w = 2b + 13$, blijkt het ineens moeilijk om ervoor te zorgen dat inderdaad elke wiskundige het juiste aantal biologen kent en andersom. We moeten beter zien te begrijpen hoe we de lijntjes tussen wiskundigen en biologen moeten trekken en hoeveel daarvan nodig zijn. Om dat te proberen moeten we toch kijken naar het volgende kleinste geval, $(b, w) = (5, 23)$. Deze keer moeten we echt de graaf tekenen en de juiste lijntjes tussen wiskundigen en biologen gaan trekken. We gaan systematisch en overzichtelijk te werk: we scheiden de wiskundigen van de biologen en we gaan alleen nog maar lijntjes tussen een wiskundige en een bioloog tekenen. Van de rest weten we toch al dat ze elkaar kennen.

Het is een redelijke strategie om gewoon maar te beginnen met lijntjes trekken en zo lang mogelijk de eisen in stand te houden, dus dat elke wiskundige vier biologen kent en elke bioloog negen wiskundigen. Hoe doe je dat? Je kunt beginnen met vanuit elke wiskundige vier lijntjes te trekken naar vier biologen en zo evenredig mogelijk de lijntjes over de vijf biologen te verdelen. Zo garandeer je dat elke wiskundige vier biologen kent. Je kunt ook juist telkens negen lijnen vanuit een bioloog trekken om ervoor te zorgen dat elk negen wiskundigen kent. We zouden klaar zijn als we met beide strategieën precies dezelfde lijnstukken zouden krijgen.

Ik raad je aan die strategie maar eens te proberen op onze tot nu toe onvolledige graaf. Je merkt dat het niet gaat lukken. Als je vanuit elke wiskundige vier lijnen trekt krijg je namelijk $23 \cdot 4 = 92$ lijnen, maar als je er vanuit elke bioloog negen trekt krijg je er slechts $5 \cdot 9 = 45$. Dit kunnen dus nooit dezelfde lijntjes worden!

We kunnen deze lijntjes tussen een bioloog en een wiskundige natuurlijk ook algemeen tellen. Als er $b$ biologen zijn die elk negen wiskundigen moeten kennen en $w$ wiskundigen die elk vier biologen moeten kennen, dan moeten er vanuit de wiskundigen gezien $4w$ lijntjes getrokken worden, vier per wiskundige. Vanuit de biologen gezien krijgen we juist $9b$ lijntjes, negen per bioloog. Omdat dit bij een congres dat aan alle eisen voldoet gewoon dezelfde lijntjes moeten zijn, moet het aantal natuurlijk gelijk zijn, dus geldt $4w = 9b$, ofwel $b=\tfrac{4}{9}w$. Dat blijkt precies het tweede inzicht dat we nodig hadden.

We hebben nu de twee lineaire vergelijkingen $b=\tfrac{4}{9}w$ en $w = 2b + 13$. Substitueren we die eerste in de laatste, dan krijgen we $w=2\cdot\tfrac{4}{9}w+13=\tfrac{8}{9}w+13$ , dus $\tfrac{1}{9}w = 13$. We concluderen dat $w = 9 \cdot 13 = 117$. De enige mogelijkheid voor het aantal wiskundigen is dus $117$, met als aantal biologen $b=\tfrac{4}{9}w=\tfrac{4}{9}\cdot 9\cdot 13=4\cdot 13=52$.

Als je een deelnemer aan de Wiskunde Olympiade was, zou je nu natuurlijk snel $117$ invullen en doorgaan. De vraag geeft immers al weg dat het überhaupt mogelijk is zo’n congres te vormen. Strikt genomen weten we echter alleen dat er maximaal één mogelijkheid is. We zouden eigenlijk nog moeten verifiëren dat we de lijntjes tussen de $117$ wiskundigen en $52$ biologen daadwerkelijk kunnen trekken. Het is een leuke oefening om dit zelf te proberen, maar ik geef nu weg dat dit makkelijk kan. Maak dertien groepjes van elk vier biologen en negen wiskundigen. Als je er nu voor zorgt dat elke wiskundige precies de $4$ biologen uit zijn groepje kent, plus de overige $116$ wiskundigen en dat elke bioloog precies de $9$ wiskundigen uit zijn groepje kent, plus de $51$ overige biologen, dan kennen de wiskundigen en biologen respectievelijk $120$ en 60 mensen. Zo wordt dus aan alle eisen voldaan. We zijn klaar!

Laten we eens terugblikken op het proces. Hoe zijn we hier gekomen? We moesten eerst bedenken hoe we überhaupt konden werken aan deze opgave. Daarna hebben we gewoon doorgezet: telkens als we het ene geval volledig uitgewerkt hadden, begonnen we aan het volgende. Telkens hebben we de nieuwe informatie gebruikt om strategischer en efficiënter te werken. Door zelfs aan het veel te groot lijkende geval $(b, w) = (5, 23)$ te beginnen, kregen we het inzicht om de opgave op te lossen. We hebben dat geval niet eens afgemaakt! Als je niet opgeeft, komt het meestal vanzelf en vaak sneller dan je denkt. We hebben simpelweg door helder te blijven en niet op te geven de opgave overmeesterd!

Hopelijk ben je er ook van overtuigd geraakt dat jij ook deze opgave had kunnen kraken. Als dat zo is en je nog middelbaar scholier bent die niet in de zesde klas zit, kun je aankomende januari ook proberen de allermoeilijkste opgave van de volgende eerste ronde te kraken. Er is maar één probleem: dan staan er in de twee uur die je hebt nog elf andere opgaven op je te wachten.