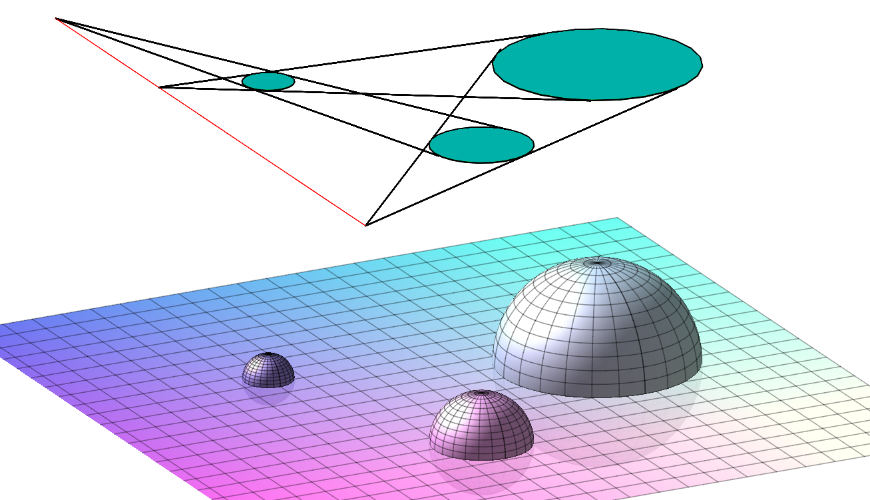
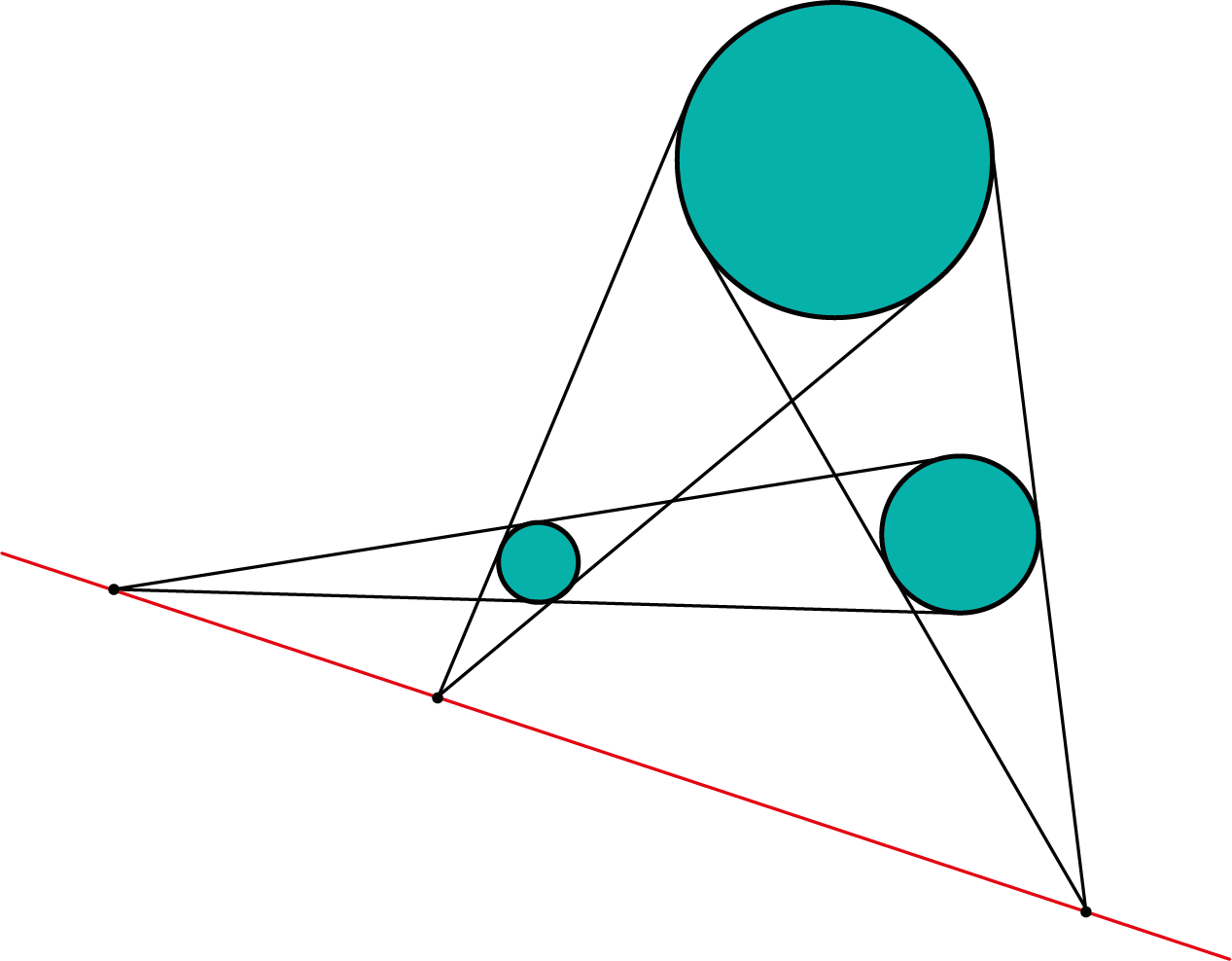
Zo luidt de cirkelstelling van Monge: gegeven zijn 3 cirkels in het vlak met verschillende straal, en zo gelegen dat er geen cirkel volledig in een andere ligt. Voor elk paar cirkels zijn er dan twee rechten die uitwendig raken aan beide cirkels, en die elkaar snijden in een punt. Indien we de cirkels twee per twee samennemen, dan vinden we zo drie punten. De stelling van Monge zegt dat deze drie punten op een rechte liggen. Zie figuur 1.

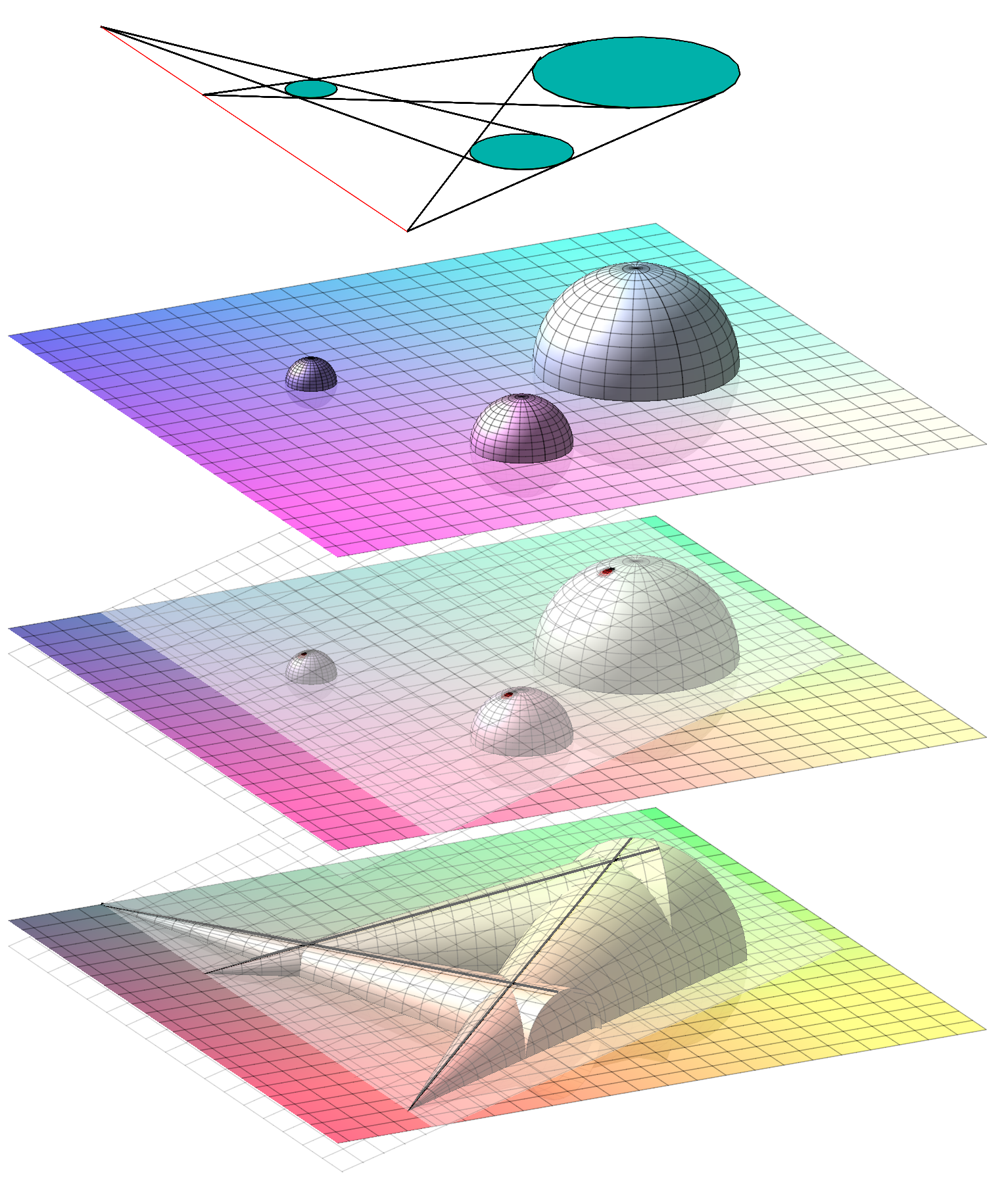
Gaspard Monge publiceerde zijn resultaat in 1798 in zijn Géométrie Descriptive. Het onderstaande bewijs staat ook zo in dat boek. Het bewijs is grafisch, en vereist een derde dimensie. Stel je voor dat de drie cirkels de evenaars zijn van drie bollen. Leg op die drie bollen een vlak. Als je nu die bollen twee per twee samenneemt en er telkens een kegel omheenwikkelt, dan ligt dat vlak ook mooi op die drie kegels. De twee vlakken, het vlak van de stelling en dit vlak, snijden elkaar volgens een rechte, en de toppen van de kegels liggen alledrie op die rechte. Maar de drie kegels snijden het oorspronkelijke vlak precies volgens de raaklijnen aan de drie cirkels! Zie figuur 2.

In het volgende nummer bekijken we hoe de extra dimensie kan helpen om de stelling van Desargues te bewijzen.