Een dimensie meer helpt: de stelling van Desargues
Soms helpt het bij het bewijzen van een stelling in de vlakke meetkunde om de situatie te bekijken vanuit een derde dimensie. In het vorige nummer lieten we zien hoe de derde dimensie bij de tweedimensionale stelling van Monge een bijzonder elegant bewijs opleverde. Deze keer de stelling van Desargues, waarbij de extra dimensie ook meer inzicht geeft.
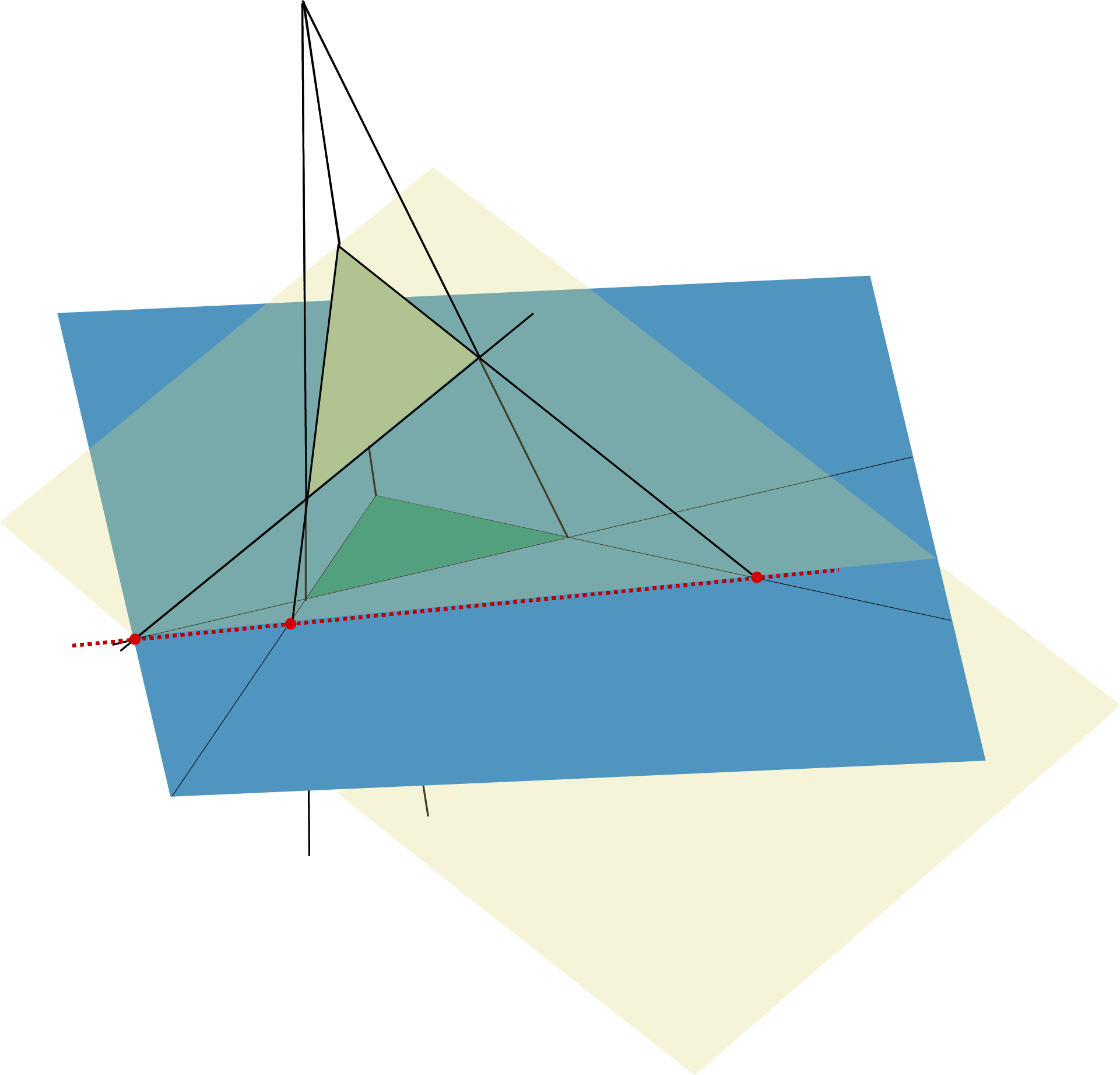
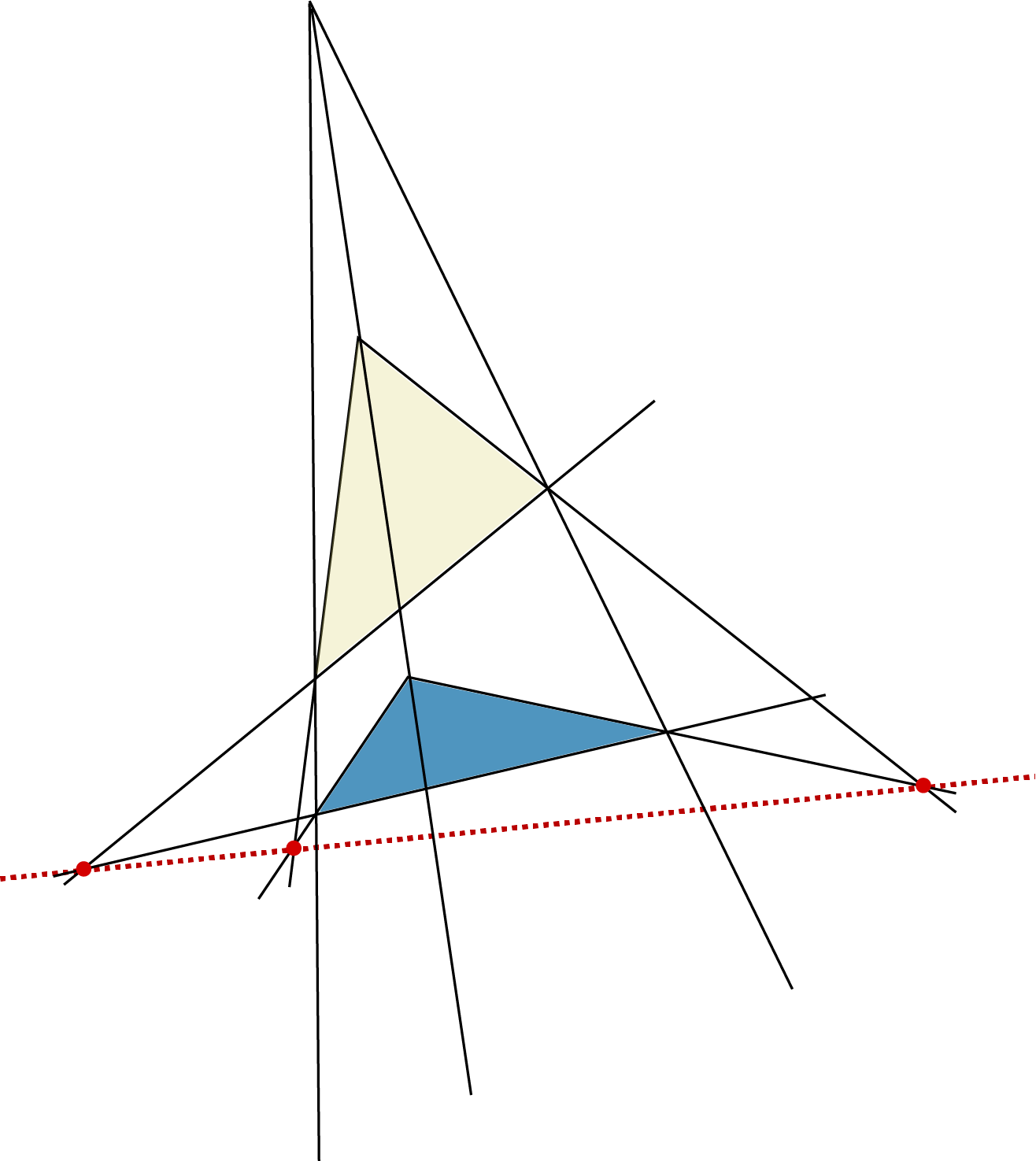
De stelling van Desargues luidt: als van twee driehoeken de drie verbindingslijnen van de corresponderende hoekpunten door één punt gaan, dan liggen de drie snijpunten van corresponderende zijden op één lijn. Zie figuur 1. Als die zijden evenwijdig zijn, dan is die lijn wat men noemt de rechte op oneindig.
De stelling wordt toegeschreven aan Girard Desargues maar werd voor het eerst gepubliceerd door Abraham Bosse in 1648. Voor het (grafische) bewijs bekijken we de tekening in figuur 1 in drie dimensies waarbij we de drie verbindingslijnen van de corresponderende hoekpunten samen met de blauwe driehoek opvatten als een piramide waarvan het grondvlak deel uitmaakt van het blauwe vlak in figuur 2. De drie hoekpunten van de gele driehoek bepalen een vlak, en dat snijdt het blauwe vlak volgens een rechte.