Ken je iemand die binnenkort 36 jaar wordt? Geef hem dan de bijzondere taart die je hierboven ziet.

Tel maar eens de getallen in een rij, een kolom, of één van de twee diagonalen bij elkaar op. Dan zie je gauw genoeg waarom deze vierkante taart leuk is voor een kersverse 36-jarige. Er zijn zelfs nog meer mogelijkheden om op de magische som 36 uit te komen, namelijk in elk van de volgende zeven 2 × 2-deelvierkanten:

Je ziet: opnieuw is de som van de getallen 36.

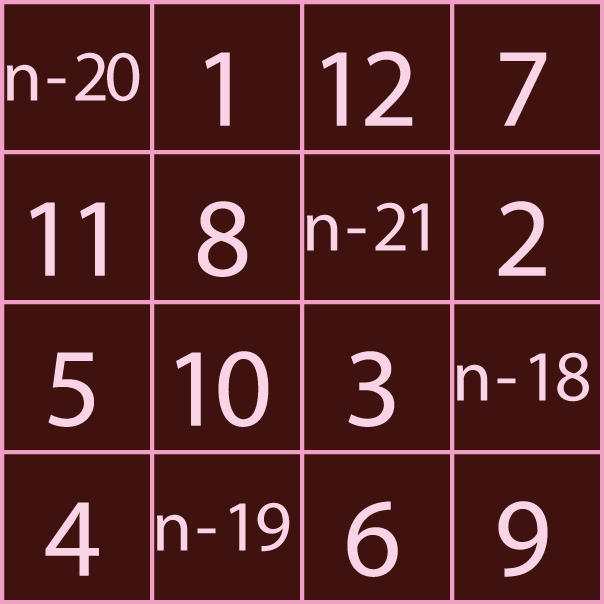Deze ‘36-eigenschap’ is toe te schrijven aan een variabele die in het vierkant verstopt zit. Bekijk maar eens het, algemene, vierkant hiernaast.

Kies je $n=$36, dan krijg je de tabel waarmee we begonnen. Waarom komt er opgeteld steeds dezelfde waarde uit? In elk van de vier rijen, vier kolommen, twee diagonaal en zeven deelvierkanten is er maar één vakje met de variabele $n$. De getallen in de vakjes waarin géén $n$ staat, zijn zo gekozen, dat de som van die getallen een bepaalde waarde geeft die er in de vakjes mét een $n$ vervolgens af wordt gehaald.

Neem bijvoorbeeld het deelvierkant linksboven ($n–$20, 1, 11, 8). De som van 1, 11 en 8 is 20. In het resterende vakje wordt deze waarde van $n$ afgehaald. Hierdoor komt er altijd het getal uit dat je voor $n$ had gekozen.

Grotere getallen

Viert iemand zijn 62ste verjaardag? Dan kun je $n=$62 kiezen:

 

De grote getallen springen nu ineens erg in het oog. Kan dit mooier? Jazeker. Neem als basis het vierkant met als magische som 34 (dus kies $n=$34).

Je ziet: nu staan precies alle getallen van 1 tot en met 16 in de zestien vakjes. In dit vierkant heb je in elke rij en in elke kolom de som (1+ 2 + 3 + … + 16)/4 = ½ × 16 × (1 + 16)/4 = 34.

Het vierkant met de variabele $n$ krijgen we op de volgende manier uit het laatste vierkant:

 

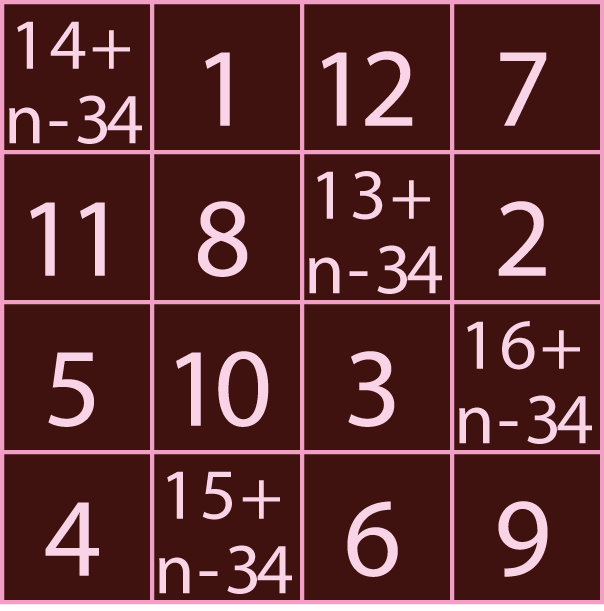
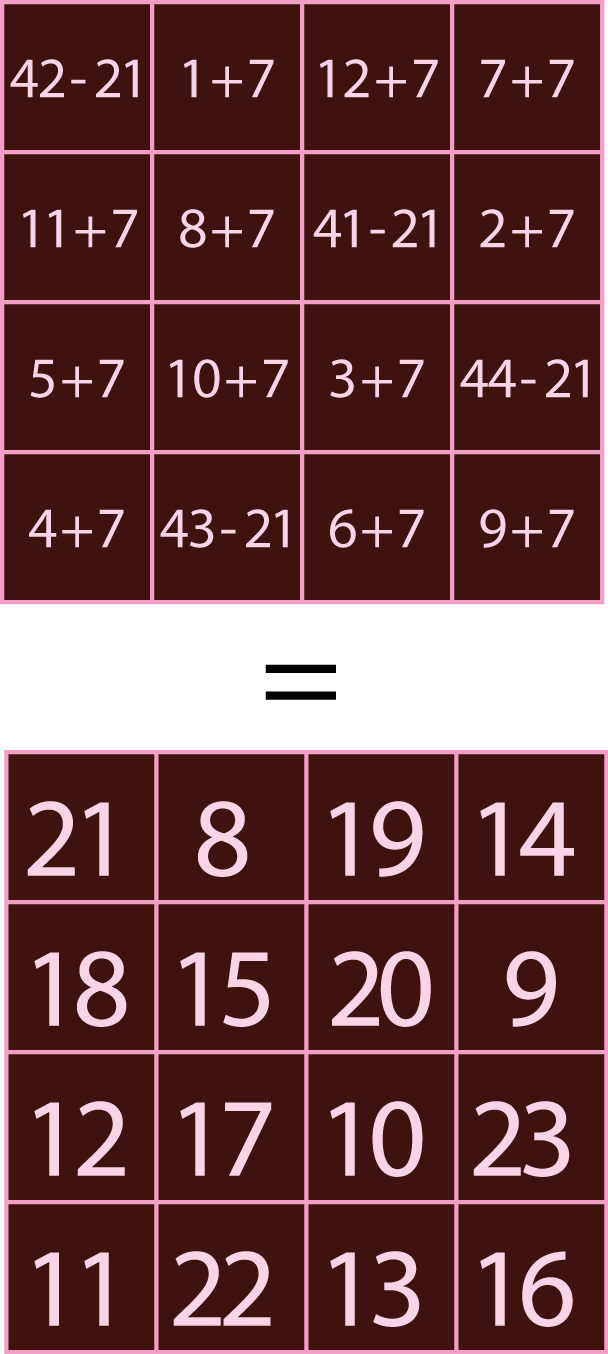Hoe kunnen we ons vierkant voor de 62-jarige nu aanpassen, zónder dat er vier grote getallen in het oog springen? Het verschil tussen de getallen 62 en 34 is 28, en dat is een veelvoud van 4. In totaal zijn er zeven veelvouden van 4 (immers, 28/4 = 7). Gebruik die veelvouden van 4 om de getallen in het magische vierkant op elkaar te laten aansluiten. In elk vakje zónder $n$ tel je 7 op, en in elk vakje mét $n$ haal je er 3 × 7 = 21 van af, om de eerste bewerking te corrigeren.

In dit magische vierkant lopen de getallen van 8 tot en met 23 netjes op, met stapgrootte 1. Rare uitschieters zijn er niet meer. En toch is de som in alle rijen, kolommen, diagonalen en deelvierkanten nog steeds 62.

Moet de magische som een getal zijn waarvoor geldt dat het verschil met 34 géén viervoud is? Haal dan het grootst mogelijke veelvoud eruit. De getallen zullen niet meer geheel oplopend zijn, maar de verschillen tussen de getallen zullen nauwelijks opvallen.

Nu ben je ook zelf in staat om een verjaardagsvierkant met leeftijd naar keuze te maken!