
Een vierkant vullen met vierkanten
Hierboven zijn twee figuren afgebeeld (van het omslag van de papieren Pythagoras). Links staat een vierkant dat is opgevuld met kleinere vierkanten. Daar omheen is een vlakvulling getekend met vierkanten.
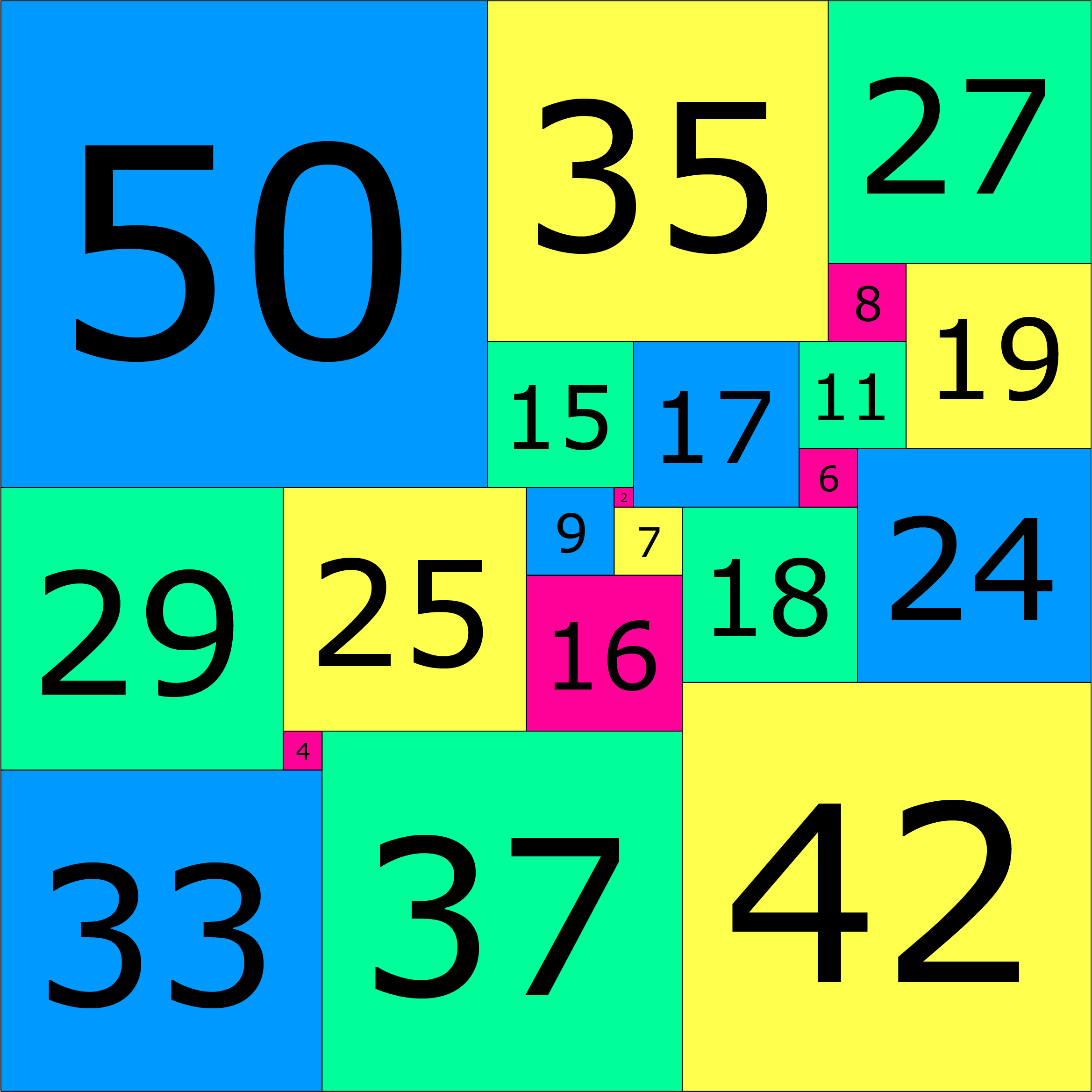
Figuur 1
In 1978 vond de Nederlander Arie Duijvestijn het kleinste vierkant dat gevuld kan worden met vierkanten met verschillende afmetingen. In figuur 1 staat hetzelfde vierkant, maar dan met de afmetingen van de zijden.
Om een dergelijk vierkant te berekenen kun je in principe een computer de zijden van de vierkanten als invoer geven en vervolgens de computer alle combinaties van die vierkanten laten berekenen. Dit is echter een zeer omslachtige en tijdrovende manier van werken. Er zijn twee manieren die veel efficiënter zijn: netwerken en algebraïsch. Hieronder ga ik dieper in op de algebraïsche methode. Netwerken is wat natuurkundiger.
Om via de algebraïsche methode een vierkant (of rechthoek) te vinden dat gevuld is met vierkanten met verschillende afmetingen maak je eerst een schets van zo'n vierkant of rechthoek. Ik ben in figuur 2a uitgegaan van vierkanten met afmetingen $1, 3, 4, 5, 7, 8, 11, 12, 13, 15, 16$ en $17.$

Figuur 2a
Vervolgens wis ik alle afmetingen en vul ik het de figuur aan met een aantal vierkanten, zodat er een rechthoek ontstaat. (Geheel rechts zijn een blauw, geel en groen vierkant toegevoegd.) We noemen één van de zijden $a$ (oorspronkelijk afmeting $1),$ en een andere $b$ (oorspronkelijk afmeting $3).$ Het blijkt dat we alle zijden van de andere vierkanten in figuur 2b kunnen uitdrukken in $a$ en $b.$ In het algemeen starten we met meerdere zijden als onbekenden.

Figuur 2b
Maar uiteindelijk zijn er evenveel vergelijkingen als onbekenden en kan het stelsel worden opgelost. In dit geval vinden we a = 11 en b = 34. De afmetingen van de rechthoek zijn 656 × 371. We hebben geluk: alle 15 gebruikte vierkanten hebben verschillende afmetingen (zie figuur 2c). Helaas hebben we niet het geluk om een vierkant te vinden. Daarvoor moeten we dit procedé een aantal keren herhalen met verschillende schetsen. Op de webpagina squaring.net kun je deze rechthoek terugvinden onder tiling by squares, squared rectangles, SPSR's order 15.

Figuur 2C
Vlakvulling en betegeling
Eerst moet er iets gezegd worden over het begrip vlakvulling, ook wel betegeling.

Figuur 3a
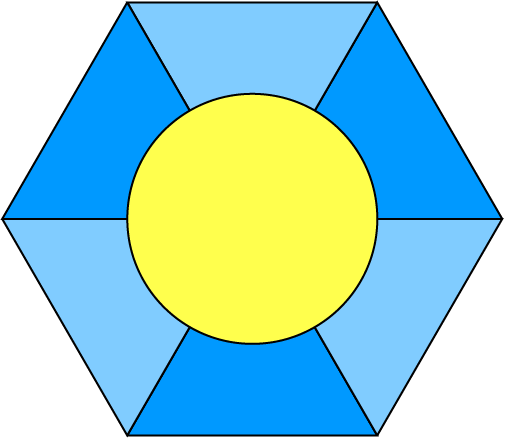
Figuur 3b

Figuur 3C
We bekijken eerst een voorbeeld. In figuur 3a zijn een trapezium, waarbij een lijnstuk is vervangen door een cirkelboog (blauw) en een cirkel (geel) getekend. Door 6 trapezia en een cirkel te combineren ontstaat een zeshoek, zoals getekend in figuur 3b. Met deze zeshoeken kan figuur 3c worden gelegd.
Nu volgen de definities. De trapezium en cirkel noemen we de stempeldelen. De zeshoek noemen we het stempel. In figuur 3c stempelen we met het stempel van figuur 3b het totale oppervlak. Figuur 3 heet een betegeling. Er geldt
Elk stukje van het oppervlak is bedekt.
Geen enkel stukje oppervlak is dubbel bedekt.
Het stempel bevat slechts een eindig aantal stempeldelen
Het stempel heeft een eindige oppervlakte
De laatste twee eisen zijn alleen maar toegevoegd om een aantal ongewenste situaties uit te sluiten, zoals het plaatsen van evenwijdige lijnen op een vlak.
Pythagoreïsche betegeling en generalisatie.

Figuur 4a
|

Figuur 4b
|

Figuur 4C
|
We gaan uit van vierkante tegels. Als alle tegels dezelfde afmeting hebben, dan kun je een betegeling maken zoals in het figuur hiernaast. Maar als je twee verschillende maten vierkante tegels hebt, dan kun je een verrassend patroon leggen, waarbij je evenveel van beide tegels gebruikt. Deze betegeling heet de Pythagoreïsche betegeling. We kunnen ook met drie soorten tegels werken (voor het gemak afmetingen $1, 2$ en $3).$

Figuur 5
Hierboven staan de stempels die gebruikt worden voor de betegelingen voor respectievelijk twee en drie verschillende vierkanten. Wat valt op? In beide gevallen heeft het stempel de vorm van een rechthoek waar een andere rechthoek uitgeknipt is. Het is inderdaad mogelijk om met een dergelijk stempel een betegeling te maken. Zie de figuren 6a en 6b.

Figuur 6a
|

Figuur 6b
|
De achtergrond op de achterkant bevat het stempel in figuur 7:
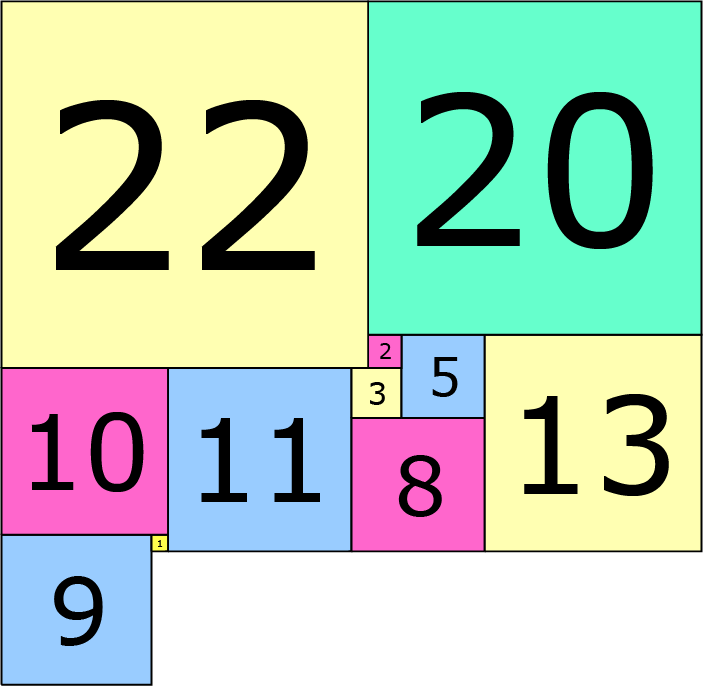
Figuur 7
Hiermee kan de achtergrond worden gecreëerd.

Figuur 8
Het is veel eenvoudiger om een betegeling te maken met een stempel bestaande uit verschillende vierkanten, dan een rechthoek te maken met verschillende vierkanten. Probeer zelf eens een betegeling te maken!
In 1917 werd de volgende puzzel van Henry Dudeney gepubliceerd.
Mevrouw Perkins krijgt met Kerstmis een patchwork (een handwerk bestaande uit kleine lapjes stof) met afmeting 13 × 13. Wat is het kleinste aantal lapjes stof als alle lapjes vierkant zijn, en gehele afmeting hebben?
De puzzel werd beroemd, en door de puzzel ging men zich afvragen of een groter vierkant patchwork van Mevrouw Perkins misschien zou kunnen bestaan uit allemaal verschillende vierkante lapjes.
Zbigniew Moroń vond in 1925 de eerste rechthoek die gevuld was met vierkanten.
