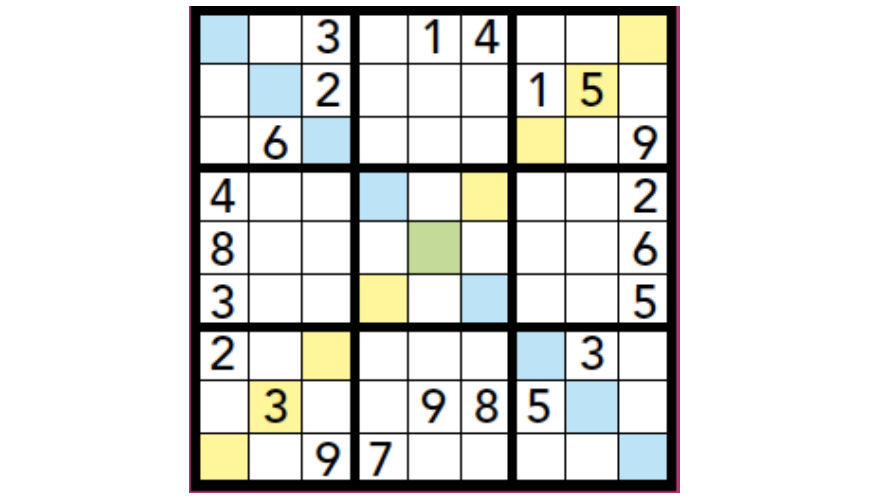
Exotische sudoku’s
Behalve de gebruikelijke sudoku-regels geldt hier ook nog dat de twee diagonalen alle cijfers 1 tot en met 9 moeten bevatten.
Aad van de Wetering en Aad Thoen, Exotische sudoku’s, 175 pagina’s, € 16.
De sudoku is een bekende puzzel waarbij op speciale wijze negen keer de cijfers 1 tot en met 9 in een diagram moeten worden ingevuld. De puzzel werd een enorme rage en heeft nog steeds een vaste plaats in allerlei kranten en tijdschriften.
Al werd de puzzel eind jaren 70 van de vorige eeuw geïntroduceerd, pas deze eeuw hebben allerlei wiskundigen zich over vragen omtrent de puzzel gebogen. Zo zijn er studies gemaakt naar het kleinste aantal cijfers dat nodig is om de puzzel nog uniek oplosbaar te laten zijn, en er zijn allerlei varianten bedacht om de puzzel aantrekkelijk te houden. Puzzelontwerper Aad van de Wetering en wiskundige Aad Thoen hebben sinds 2009 allerlei, vooral wiskundige, varianten van de puzzel bedacht.
Van de Wetering en Thoen hebben nu een boek geschreven: Exotische sudoku’s. Wat zij in dit boek presenteren, is van een heel andere orde dan de meeste varianten die in kranten te vinden zijn. Hier hebben twee fanatici de grenzen van het sudoku-design opgezocht.
In de loop der jaren werden Van de Wetering en Thoen specialisten op het gebied van de reeds ingevulde sudoku en analyseerden zij allerlei regelmatigheden van de getallenpatronen. Dit blad besteedde daar in jaargang 51 aandacht aan. In de afgelopen jaren hebben ze bij hun onderzoek een groot aantal sudoku-puzzels ontwikkeld, gebaseerd op dergelijke wiskundige eigenschappen. Deze enorme arbeid is nu in Exotische sudoku’s gebundeld.
Wild en inventief
De bedoeling van een sudoku is het invullen van een $9 \times 9$-rooster met de cijfers 1 tot en met 9. Op elke horizontale en elke verticale lijn moeten alle cijfers één keer voorkomen. De sudoku is verdeeld in 9 vierkanten van $3 \times 3$ en elk van deze vierkanten moet ook nog eens gevuld worden met alle cijfers 1 tot en met 9. Het is de kunst van de puzzelontwerper om de sudoku nét genoeg startcijfers te laten bevatten om de puzzel uniek te kunnen te oplossen.
In het nieuwe puzzelboekje worden allerlei wiskundige voorwaarden aan de sudoku opgelegd. Hierdoor zijn de puzzels een stuk gecompliceerder. Zo zijn er heel veel puzzels, waar de diagonale buren niet gelijk mogen zijn, waar pentominofiguren steeds dezelfde cijfers moeten bevatten, er gewerkt wordt met paardensprongen uit het schaakspel, en er is een variant waarbij op de diagonalen ook nog eens negen verschillende cijfers moeten staan.
De puzzels worden steeds wilder en inventiever. Er zijn rekenkundige voorwaarden (die ook wel eens in andere sudoku’s verschijnen), er zijn spiegel- en draaisymmetrische hints en een groot aantal varianten met magische deelvierkanten. Aan het einde van het boek staan allerlei interessante vormsudoku’s, $10 \times 10$-varianten en andere curiosa.
In één sudoku vormen de gegeven cijfers de eerste 22 cijfers van π, prachtig in het rond door de puzzel heen gedrapeerd. (De eerste 22 cijfers van $π$ bevatten dan ook geen 0; dat gebeurt pas in de 32ste decimaal!) Het is een wonder hoeveel van dit soort dingen de auteurs weten te bedenken.
Zelf doen
Ik ben geen specialist in het oplossen van sudoku’s. Ik weet dus ook niet hoeveel mijn bewering waard is als ik zeg dat de meeste vreselijk moeilijk zijn. Hierboven zie je één sudoku (die met de $π$-decimalen), om je een indruk te geven. Hoe dan ook staat dit creatieve hoogstandje garant voor maandenlang puzzelplezier!
