In figuur 1 wordt in detail uitgelegd hoe je in een patroon vlechtwerk aanbrengt door van alle lijnstukken strookjes te maken, en bij de snijpunten de juiste lijnstukjes uit te wissen. In figuur 2 is een patroonontwerp uit de vorige Pythagoras gebruikt om te laten zien welk resultaat deze weeftechniek geeft. Hierbij wordt een patroon omgetoverd tot een versie waarbij alle lijnen in elkaar gevlochten lijken te zijn, wat een ruimtelijk effect geeft.

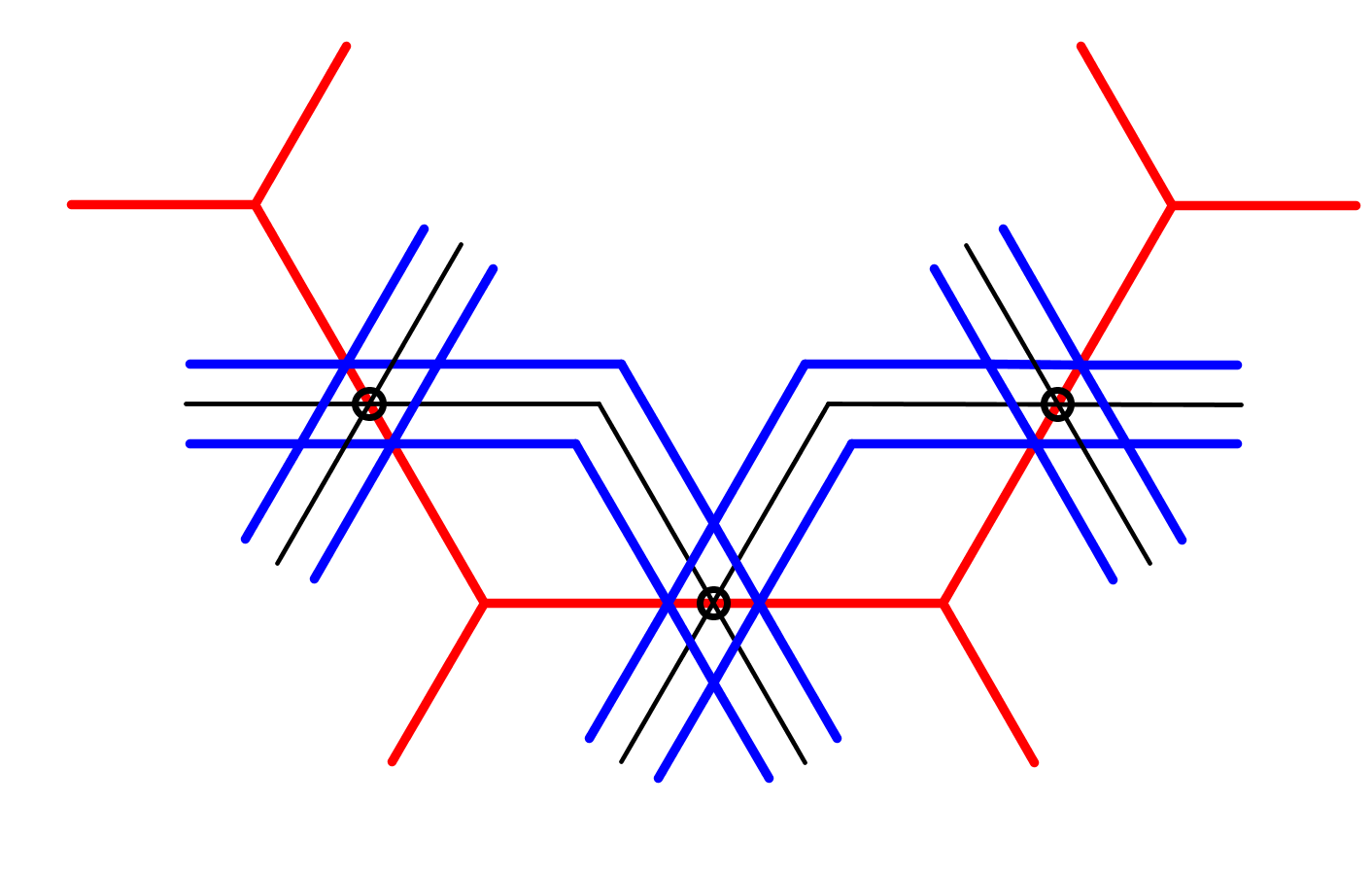
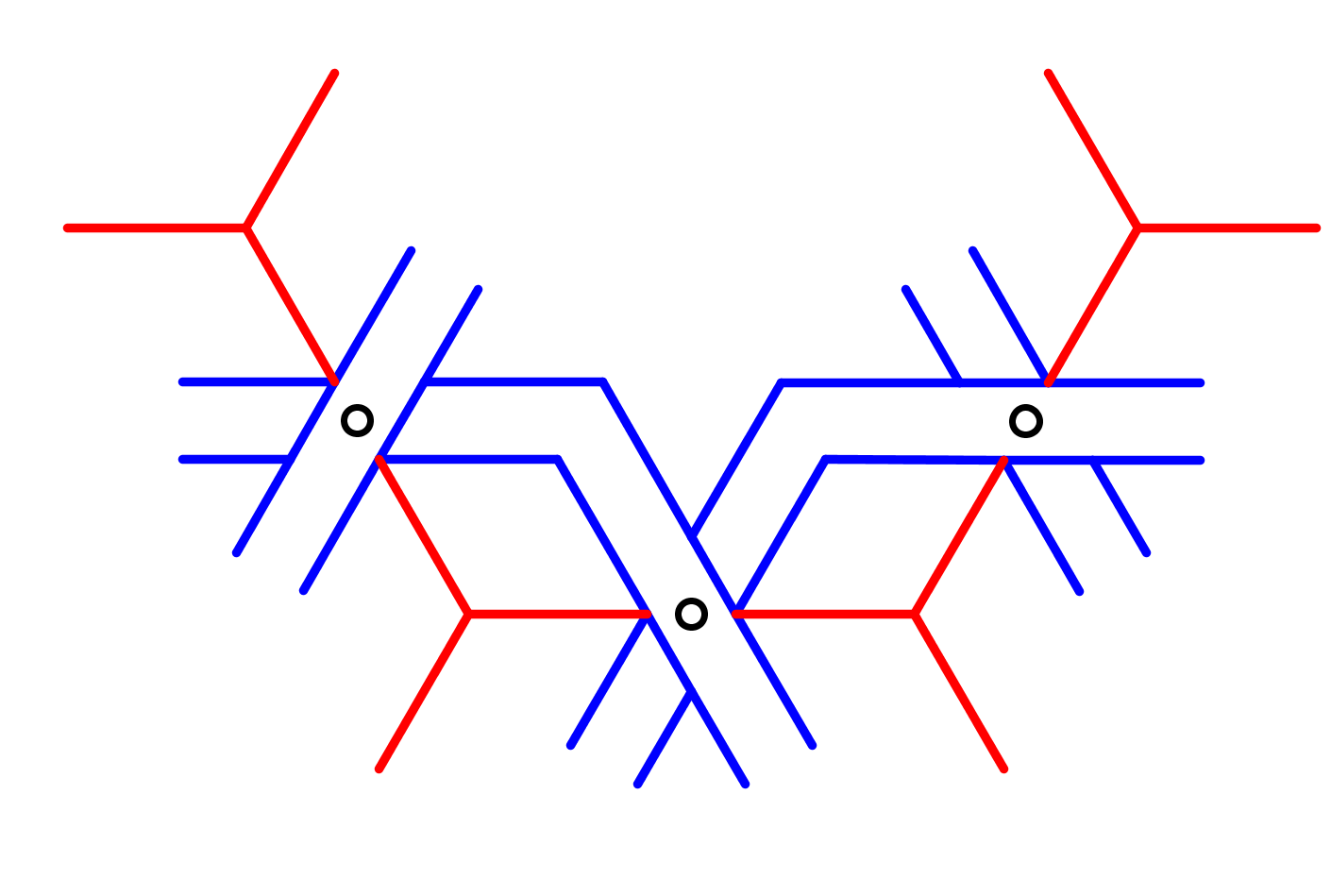
Je gaat uit van een ontwerp dat met de gireh-methode is getekend. Hier zie je daar een detail van: Op enkele rode lijnstukjes van het raster zijn zwarte lijntjes geconstrueerd die elkaar op de middens van de rode lijnstukjes snijden. Teken vervolgens langs al deze zwarte lijnstukjes van het basisontwerp aan weerszijden, op vaste afstand, evenwijdige lijntjes (hier in het blauw getekend). Zo ontstaan allemaal strookjes.

Wis bij alle kruisingen van de strookjes telkens twee lijnstukjes. Vergelijk het met een wegennet: Er ontstaan, in plaats van gelijkwaardige kruisingen, viaducten. Zorg ervoor, dat een strook beurtelings boven en dan weer onder een andere strook lijkt te gaan. Zo ontstaat het juiste vlechtwerk. Wis ook alle lijntjes van het basisontwerp.

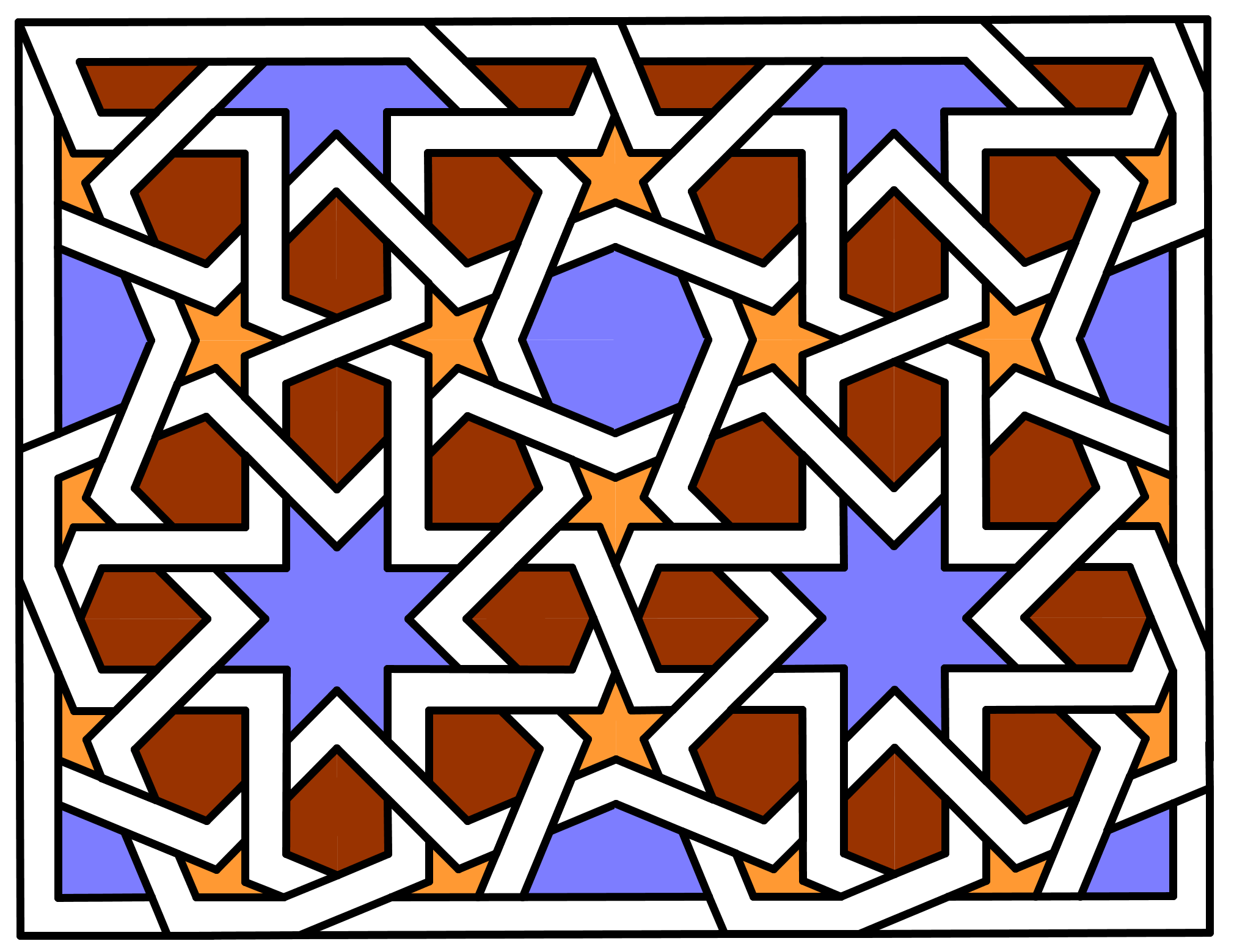
Het resultaat bij het toepassen van deze techniek op het ontwerp van figuur 5 uit Pythagoras 59-1. Verschillende strookbreedtes en lijndiktes geven een heel ander beeld. Worden heel grote strookbreedtes gekozen, dan verdwijnen de kleinste vormen uit het oorspronkelijke ontwerp bijna helemaal.

In figuur 3 zie je hoe je, door bij elke zijde van het raster niet één, maar twee punten te gebruiken, andere varianten op een patroon kunt maken waarin geometrische vormen elkaar gaan overlappen. Door vervolgens de weeftechniek weer toe te passen lijkt het alsof deze vormen in elkaar grijpen, niet zoals bij een ketting in één richting, maar over het hele vlak. Zie figuur 4. Beide technieken kunnen in principe op elk patroon dat met rasters is ontworpen worden toegepast. Hiervan zijn schitterende voorbeelden bekend.

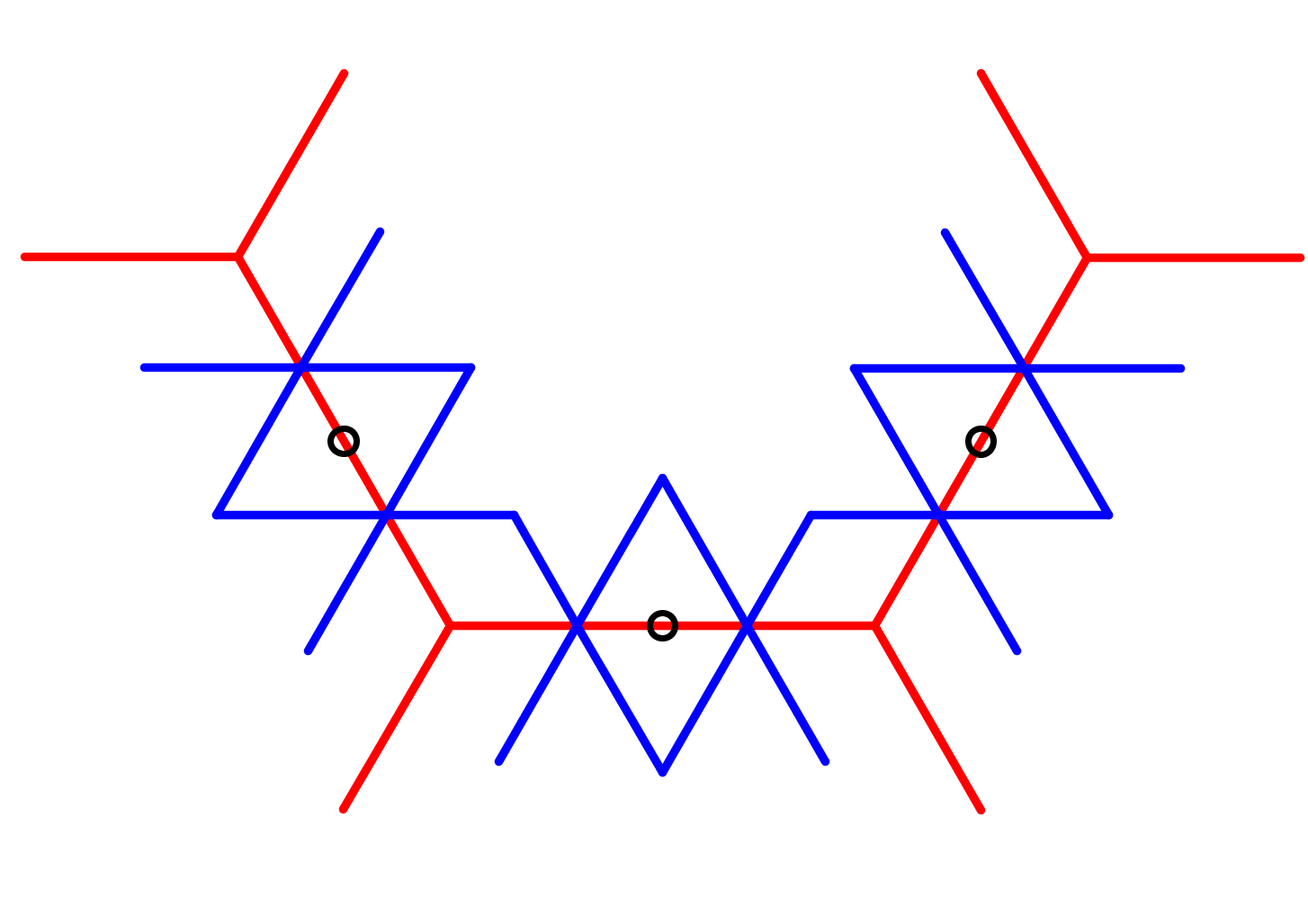
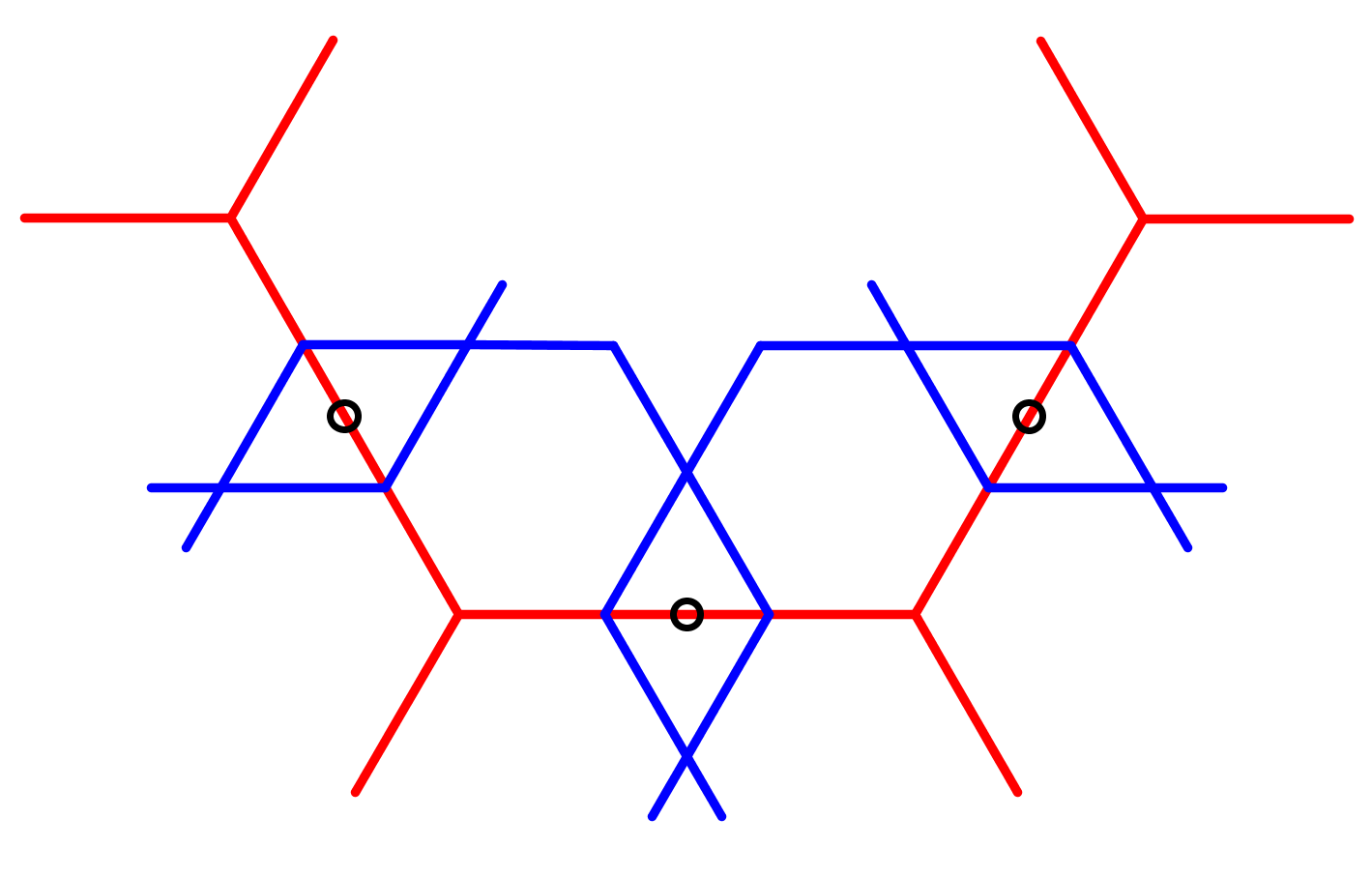
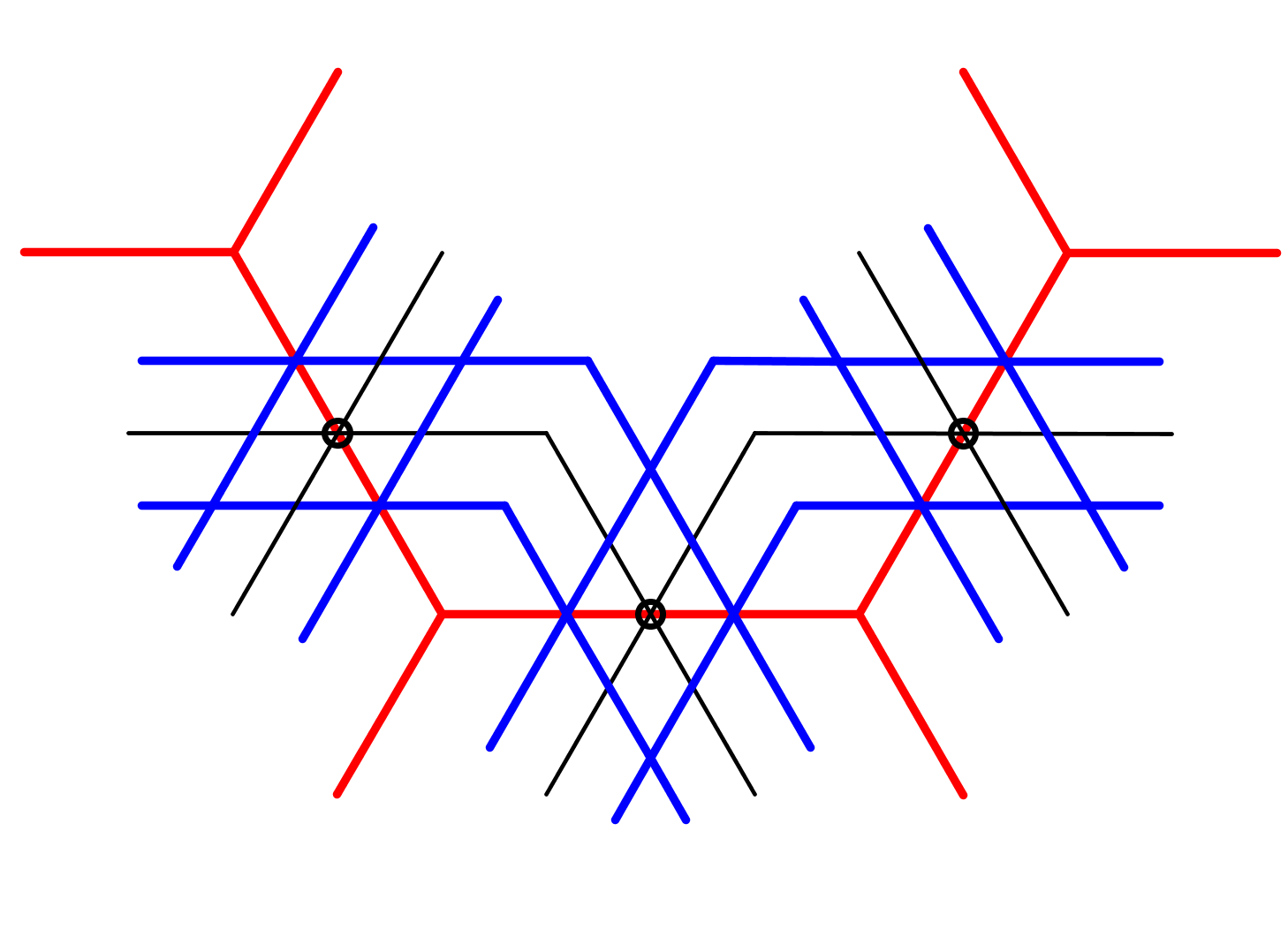
	Anders dan bij de weeftechniek wordt van de blauwe ruiten niets gewist, maar wel de helft van de andere blauwe lijnstukjes. Dit kan op twee manieren: boven variant 1, en onder variant 2. Om verwarring te voorkomen zijn ook de zwarte lijntjes gewist.
Bij de tweepuntsmethode worden op gelijke afstand van de middens van de rode lijnstukken snijdende lijnen getekend. Merk op dat deze eerste stap sterk lijkt sterk op stap 1 van de weeftechniek.
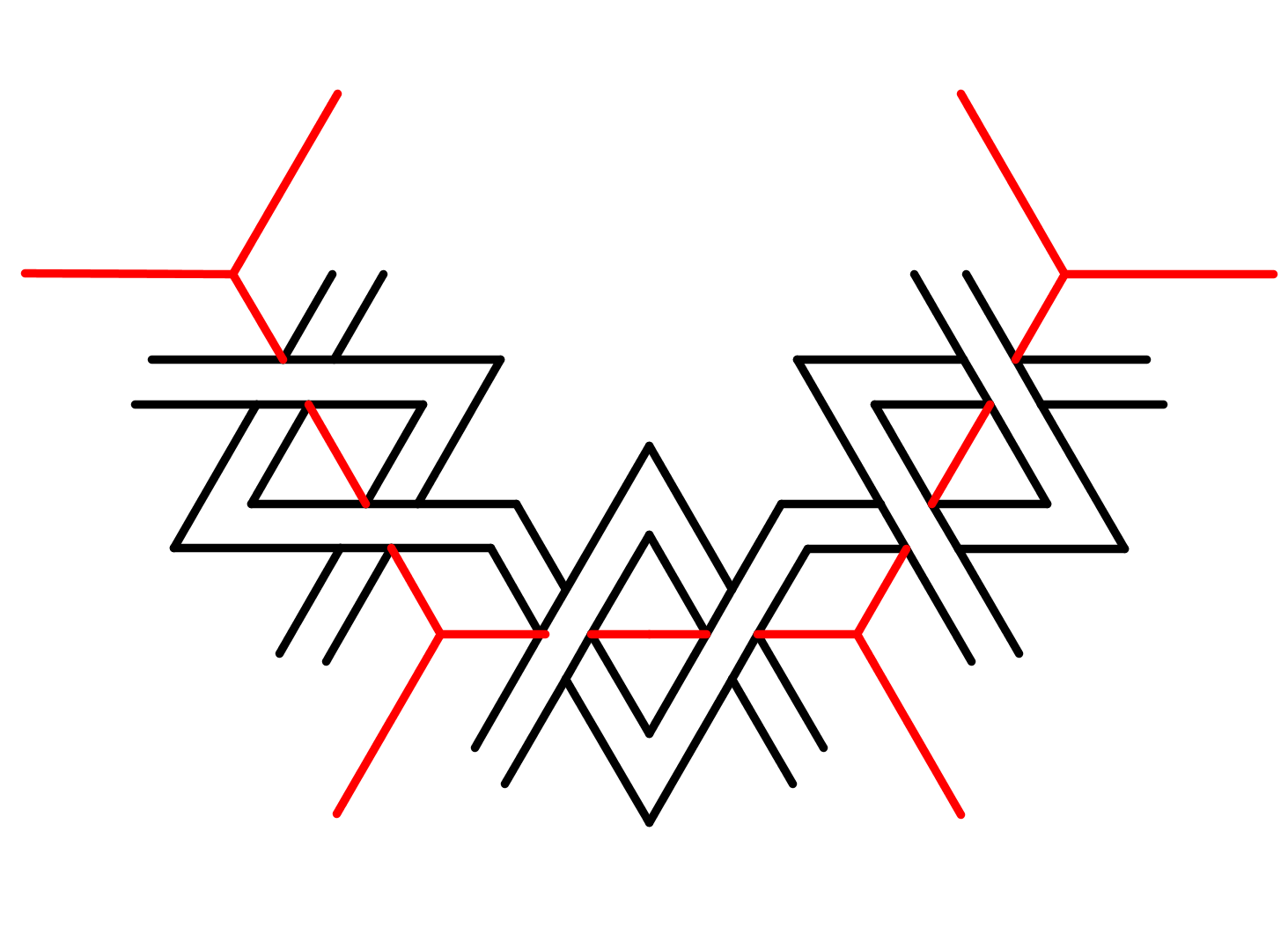
Vervolg op variant 1: Nu wordt op de blauwe lijnstukjes weer de weeftechniek toegepast, vergelijk met stap 1 en 2 van figuur 1. De blauwe lijnstukjes worden ook weer gewist. De stroken lijken nu in elkaar te haken.

Een toepassing van stap 2 variant 1 kan bijvoorbeeld dit mozaïek opleveren. De kleuren benadrukken de suggestie van ‘in elkaar haken’. In dit geval bestaat het raster uit regelmatige zeshoeken. Voor een voorbeeld van een uitwerking van variant 2, zie figuur 8.

 

Andere rasters, van heel eenvoudig tot uiterst complex

In de loop der tijd zijn enorm veel rasters gebruikt om nieuwe patronen te ontwerpen. In figuur 5 a, b en c zie je hier drie voorbeelden van, met een keuze van patronen die deze rasters opleveren. Van veel patronen valt trouwens moeilijk te achterhalen of ze daadwerkelijk met de ‘girih’-methode zijn geconstrueerd. Immers, deze methode kenmerkt zich door het gebruik van tegen elkaar aanliggende veelhoeken waaroverheen een patroon wordt bedacht, maar die oorspronkelijke veelhoeken zijn in het eindresultaat niet meer te zien! Je kunt je dus afvragen of ze eigenlijk wel gebruikt zijn, of dat een andere methode is toegepast. Er zijn echter een paar oude manuscripten met tekeningen waarop een raster te zien is. Een beroemd voorbeeld hiervan is de Topkapirol, die bewaard wordt in Istanboel. In sommige tekeningen die hierin staan zijn niet alleen de mozaïeken zelf te zien, maar ook de gebruikte rasters, waarbij een rode inkt werd gebruikt. (Dit is precies de reden waarom in dit artikel de rasters ook rood zijn gekleurd.) Zie figuur 6.

	Een raster van regelmatige achthoeken, vierkanten en strikjes (zie de rode lijnen links) levert bij de keuze van een scherpe snijhoek het mozaïek rechts op, dat in Isfahan (Iran) is te vinden.
	Om tot het mozaïek rechts te komen zijn in de twaalf- en achthoeken van het raster links rozetten geconstrueerd. De zo ontstane vormen zijn versierd met bloemmotieven. Dit tableau is gefotografeerd door prof. J.P. Hogendijk in Naïn-Yazd, Iran.
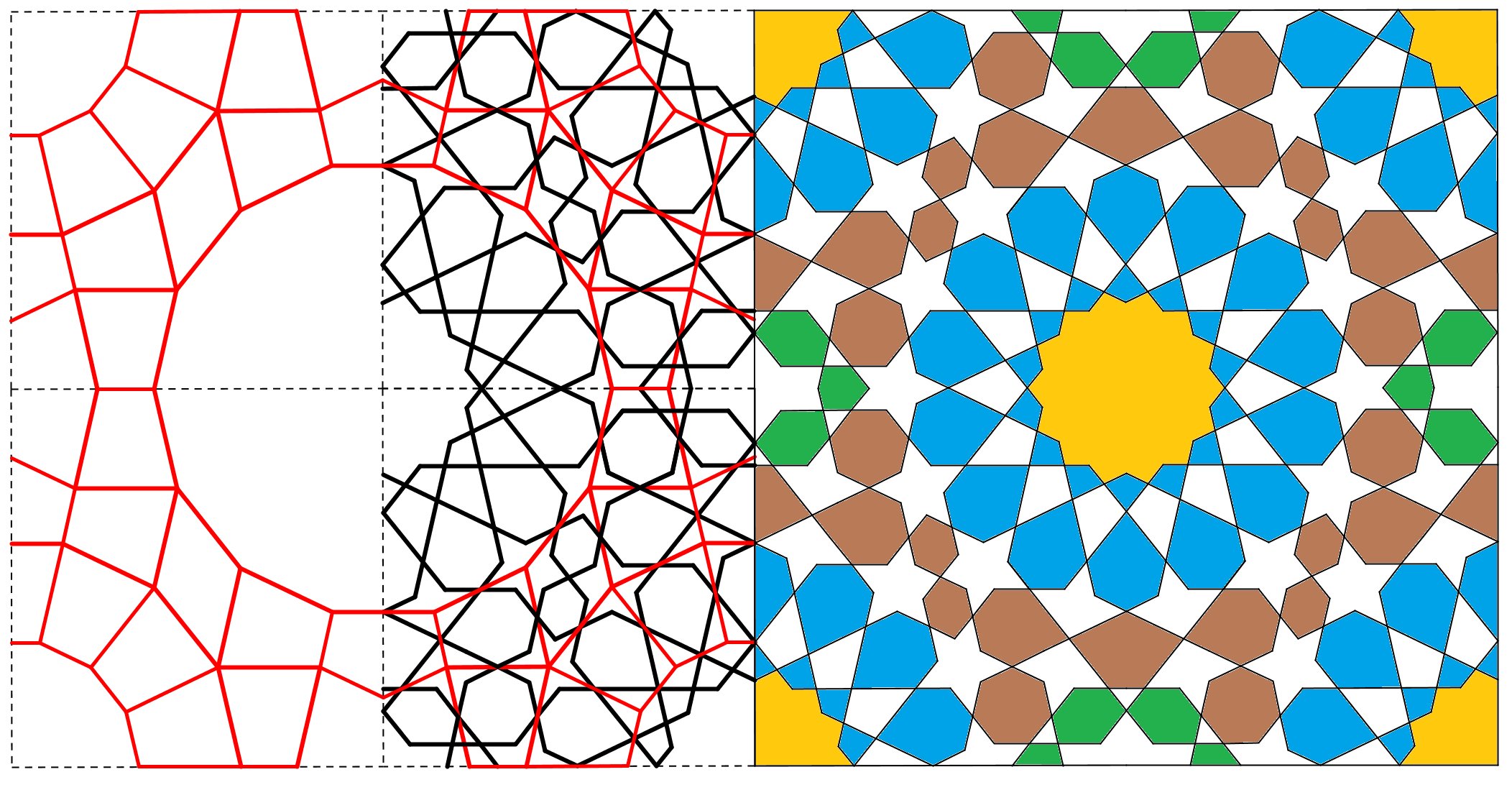
	Dit raster (links) is een stuk complexer, met regelmatige veertienhoeken en zijden van verschillende lengte. Het levert bij een keuze voor stompe snijhoeken bij de middens van de lange zijden het patroon rechts op. Dit ontwerp is ontleend aan een tekening van Joules Bourgoin, die rond 1900 tal van mozaïeken uit het Midden-Oosten reconstrueerde.

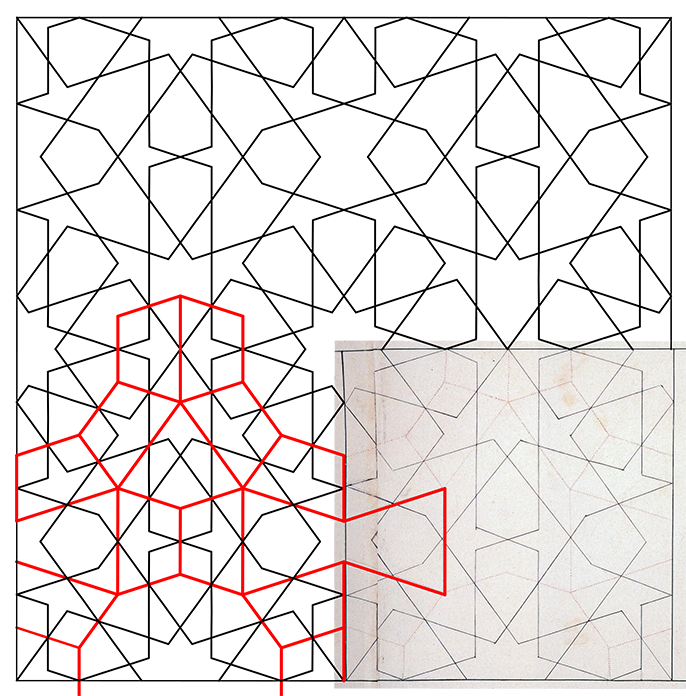
Het deel rechtsonder is een bladzijde uit de Topkapirollen. Het raster is aangegeven met dunne rode stippellijnen. Linksonder is het ontwerp digitaal gereconstrueerd. Het raster bestaat uit tienhoeken, parallellogrammen, vliegers en strikjesvormen. Wat opvalt is, dat de rode vliegervorm in de oorspronkelijke tekening niet compleet is getekend.

Van de hedendaagse patronen, die dus momenteel worden ontworpen, weten we veel beter hoe die tot stand kwamen. De ontwerper kan immers haar of zijn werkwijze zelf toelichten. Een schitterend, complex voorbeeld is het ontwerp van Jay Bonner dat hij speciaal voor dit artikel ter beschikking stelde. Zie figuur 8. Op vernuftige wijze brengt hij vijftien-, dertien- en zevenpuntige sterren samen in één patroon. Hij gebruikt hiervoor een raster van gelijkvormige uitgerekte zeshoeken waarbinnen hij een tweede, complex raster van kleinere veelhoeken construeert (figuur 7). In dit raster, dat wel iets wegheeft van een zeepbelpatroon, gebruikt hij de tweepunts-ontwerpmethode op de wijze van variant 2 in figuur 3, stap 1. Zo lukt het hem om in het eindontwerp ook regelmatige vijfhoeken binnen onregelmatige vijfhoeken van het raster te construeren.De paar tekeningen uit oude manuscripten bewijzen natuurlijk niet dat de meeste andere tekeningen ook met rasters zijn ontworpen. Voor de eenvoudiger patronen zijn rasters vaak ook helemaal niet nodig. Bij complexere patronen is er soms onenigheid tussen onderzoekers over de gebruikte methode. Dat levert interessante discussies op. Zekerheid zullen we waarschijnlijk nooit krijgen over de ontwerpmethode, wat het onderwerp ook weer een geheimzinnig tintje geeft.

Het deel rechtsonder is een bladzijde uit de Topkapirollen. Het raster is aangegeven met dunne rode stippellijnen. Linksonder is het ontwerp digitaal gereconstrueerd. Het raster bestaat uit tienhoeken, parallellogrammen, vliegers en strikjesvormen. Wat opvalt is, dat de rode vliegervorm in de oorspronkelijke tekening niet compleet is getekend.	Het mozaïek dat Jay Bonner ontwierp op basis van het raster van figuur 7 van deze tekening is te zien. Dit ontwerp is een voorbeeld van het principe van aangrenzende getallen, waarbij het aantal punten voor de twee primaire sterren één hoger en één lager is dan het aantal dat typerend is voor deze patroonfamilie. In dit geval is het typerende getal 14.

Twee fascinerende patronen met zevenvoudige symmetrie-eigenschappen

De zevenvoudige draaisymmetrie in een patroon spreekt tot de verbeelding, juist omdat die niet veel voorkomt: zowel zevenpuntige sterren als regelmatige zevenhoeken kom je zelden tegen in mozaïeken. Twee-, drie-, vier-, en zesvoudige draaisymmetrie zie je het meest. Daarnaast komt de zojuist genoemde achtvoudige draaisymmetrie veel voor, vooral in het westen van Noord-Afrika en Zuid-Spanje. Vijf- en tienvoudige symmetrie vind je juist veel in het Midden-Oosten.

Het is ook niet eenvoudig om zevenvoudige symmetrie te construeren in het platte vlak. Het is zelfs bewezen dat je alleen met een passer en een liniaal onmogelijk een perfect regelmatige zevenhoek kunt construeren! Maar er bestaan wel constructies die zevenhoeken opleveren die bijna precies regelmatig zijn. De fout is met het blote oog niet te zien.

Verder is zevenvoudige symmetrie van het complete platte vlak onmogelijk, maar dit geldt ook voor vijf- en achtvoudige symmetrie. Het is bewezen dat complete patronen op het platte vlak die schuifsymmetrie hebben alleen twee-, drie-, vier- en zesvoudig rotatiesymmetrisch kunnen zijn. Maar in patronen kunnen wel regelmatige zevenpuntige sterren of zevenhoeken worden opgenomen. Hiervoor zijn dan rasters nodig met zevenhoeken, of in ieder geval met hoeken waar zevenhoeken mooi oppassen. Van dit laatste is figuur 5c een goed voorbeeld. Als je goed kijkt, zie je dat een aantal bruine vormen regelmatige zevenhoeken zijn! Als afsluiting zie je nu nog twee andere interessante, eeuwenoude voorbeelden. Ze tonen niet alleen hoe je zevenvoudige symmetrie kunt bereiken in een patroon, maar ook meer algemeen hoe ongelofelijk veel mogelijkheden de methode met rasters biedt!

1) Een patroon in de Noordelijke Koepel van de Vrijdagmoskee in Isfahan met regelmatige zevenhoeken.

Het meest eenvoudige raster is een raster van vierkantjes. Een ander eenvoudig raster bestaat uit zeshoeken, dit noemen we ook wel honingraat. Met een honingraatraatraster zijn heel veel mozaïeken ontworpen. Zie bijvoorbeeld figuur 4.

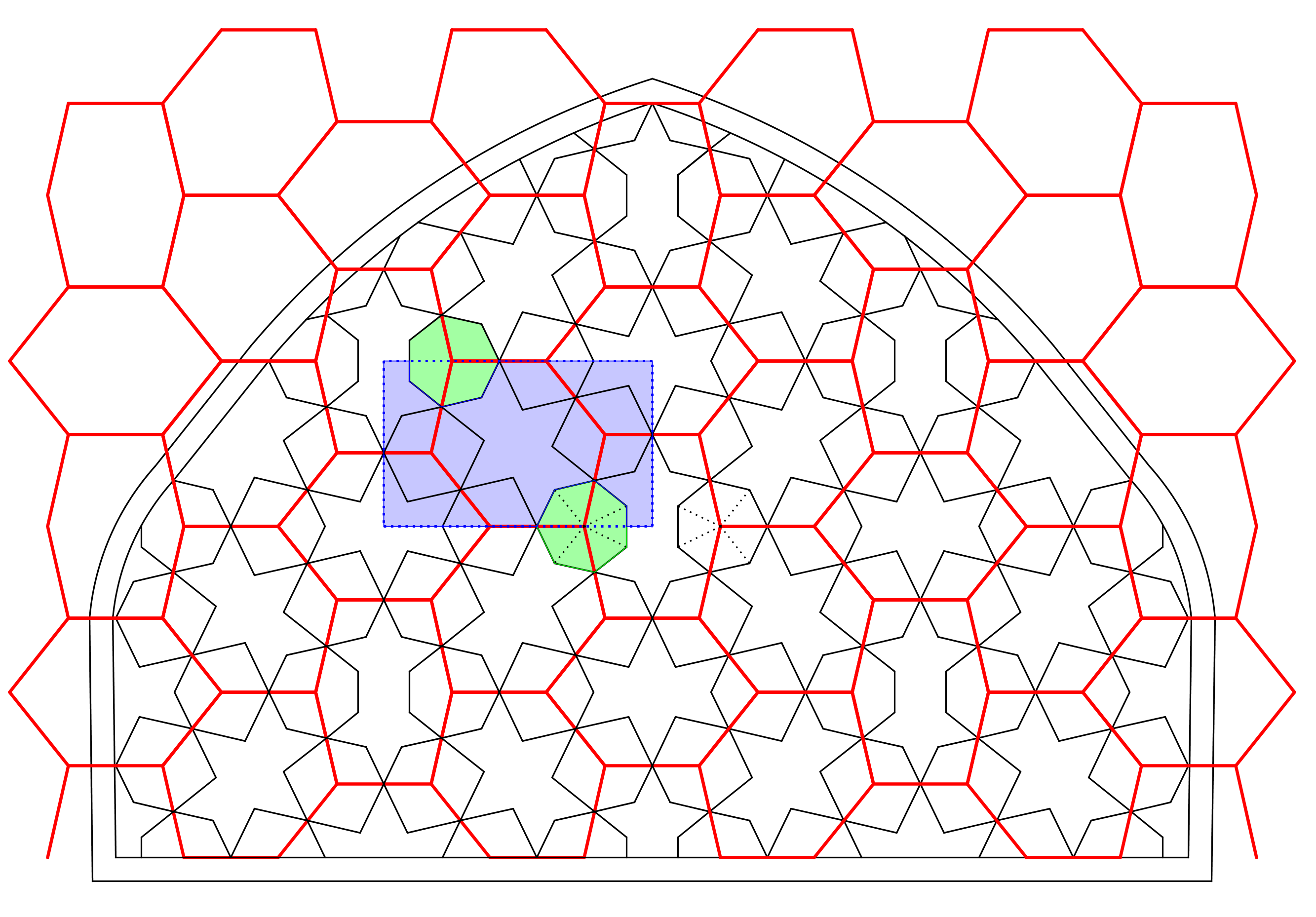
Rond het jaar 1000 bedacht iemand een variant op de honingraat. Zij of hij koos in plaats van hoeken van 120°, hoeken die allemaal een veelvoud zijn van een zevende van 180° en kon hiermee een patroon maken met regelmatige zevenhoeken. Hoe dit is gedaan zie je in figuur 9a. Dit idee is in Isfahan, in de Vrijdagmoskee, op een portaal in stucwerk uitgevoerd (figuur 9b). Professor J.P. Hogendijk uit Utrecht vond hetzelfde patroon in een Perzisch manuscript dat in Parijs bewaard wordt. In dit manuscript is de groene rechthoek uit figuur 9a getekend, inclusief het raster. Het is een bijzondere ontdekking dat een tekening van 400 jaar oud (waarschijnlijk gaat het om een handgemaakte kopie) die in Parijs bewaard wordt blijkt te gaan over een mozaïek op een moskee in Isfahan van 1000 jaar oud!

Het gestuukte mozaïek van dit patroon, te vinden in de Vrijdagmoskee van Isfahan. Foto Tom Goris.	Het rode raster is een zodanig vervormde honingraat, dat zevenhoeken kunnen worden geconstrueerd. Opvallend is, dat er twee typen zeshoeken in het raster verwerkt zijn, de meest voorkomende is zowel in ‘liggende’ als in ‘scheve’ positie gebruikt.

2) Een patroon met zevensterren op de Imam Yahyah Moskee, Mosul (vernietigd door IS)

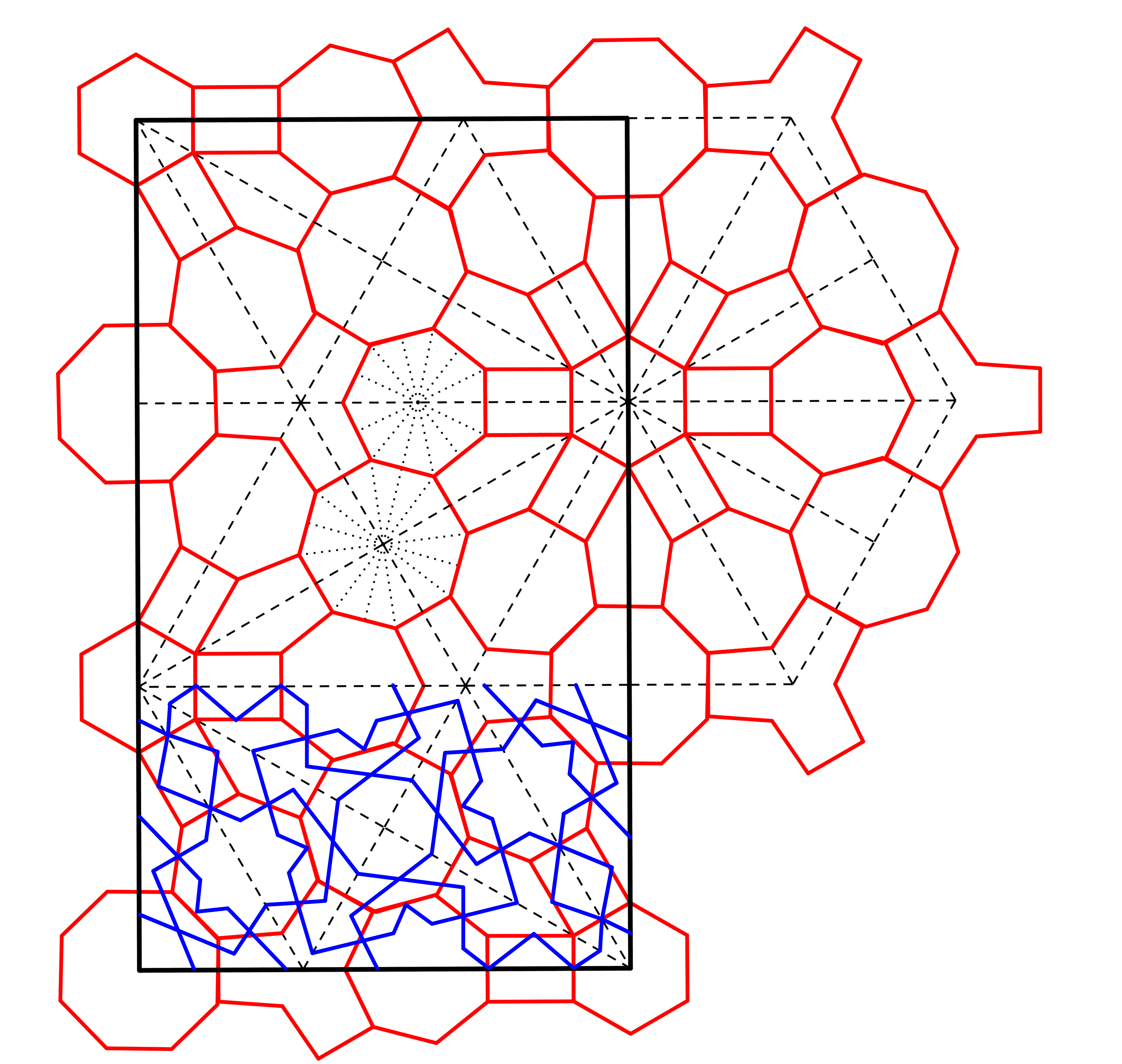
In Mosul (Irak) stond langs de rivier de Tigris een eeuwenoud mausoleum waarop reliëfs van geometrische patronen met zevenpuntige sterren waren gestuukt. Helaas is dit mausoleum in 2014 door IS vernietigd.  Er zijn wel foto’s bewaard gebleven, zie figuur 10a. Een bijpassend raster is te zien in figuur 10b. Maar of dit patroon daadwerkelijk met dit raster is ontworpen is niet zeker. Als dit wel zo is geweest, heeft de ontwerper het raster op een creatieve manier gebruikt: Door de middens van sommige zijden van de veelhoeken waaruit het raster is opgebouwd, zijn meestal wel, maar soms ook niet twee elkaar snijdende lijnen getrokken en alleen bij de achthoeken is de tweepuntstechniek toegepast. Zo zijn interessante vormen in het patroon ontstaan. Met hetzelfde raster kunnen ook andere patronen worden ontworpen, dat zou je zelf kunnen uitproberen.

Mozaïek op het Imam Yahyah Mausoleum, Mosul, Irak. Foto Archnet.	Een bijpassend grid in rood. De zwarte stippellijnen zijn symmetrieassen, die het vlak verdelen in halve gelijkzijdige driehoeken. Het is trouwens onmogelijk om hierop zowel regelmatige achthoeken als regelmatige zevenhoeken te construeren; er is een klein beetje gesjoemeld.

Tot slot

Dit is een overzicht-in-vogelvlucht van een ontwerptraditie met een eeuwenlange geschiedenis. Er valt heel veel meer over te vertellen. Dit blijkt wel uit het feit dat in 2017 een boek van 600 pagina’s uitkwam, waarin honderden mozaïeken worden gepresenteerd, en waarin het hierboven besproken mozaïek uit Mosul niet eens voorkomt. Zelfs dit enorme boek is dus niet compleet!

Hopelijk doet dit verhaal je met een meer onderzoekende blik kijken naar de geometrie die in al deze mozaïeken huist en heb je gemerkt dat er heel wat meetkundig inzicht bij komt kijken. Misschien wil je zelf aan de slag, en gaan ontwerpen met rasters? Ikzelf heb gemerkt dat dat nog het leukst is: Zelf ontwerpen, al was het alleen maar om hierdoor met nog meer bewondering te kijken naar alle schitterende, kleurrijke mozaïeken die de ontwerpers in het verleden hebben gemaakt!

Bronnen

• J.P. Hogendijk, Middeleeuwse Islamitische Geometrische Ornamentiek, http://www.jphogendijk.nl/publ/Ornamentiek.pdf

• Jay Bonner, Islamic Geometric Design