In Amerika heeft het Black-spel een korte glorietijd gekend in 1960. Het werd door de studenten van het Massachusetts' Institute of Technology zeer vaak en zeer verwoed gespeeld. Het was een uitvinding van een van hen, William L. Black. De korte duur van die glorietijd is geen gevolg van het simpele karakter van dit spel. Ieder van juUie speelt bijvoorbeeld een poosje lang het befaamde Boter-kaas-en-eieren-spel, maar lang duurt dat nooit, omdat dat spelletje in wezen te kinderachtig is. Met het Black-spel is dat beslist niet het geval. Het is een boeiend spel, dat vele intrigerende problemen opwerpt. Je zult er wel veel plezier mee kunnen hebben. Nee, die korte glorietijd is te wijten aan de spitsvondigheid van een van Black's medestudenten, Elwyn R. Berlekamp. Dat jongmens vond namelijk een verbluffend eenvoudige strategie voor het Blackspel, waardoor de uitslag van het spel eigenlijk al beshst was, zodra uitgemaakt was, wie de eerste zet mocht doen. En toen was de aardigheid eraf. Je vindt die strategie verderop in dit nummer vermeld en besproken. Neem echter een goede raad aan: kijk er niet naar (tenzij je verschrikkelijk nieuwsgierig bent). Speel het spel liever. Het is het waard. Het Blackspel wordt op een rechthoekig en in vierkantjes verdeeld veld gespeeld. De afmetingen van dat veld doen er niets toe. Je kunt bijvoorbeeld als speelveld een acht-bij-acht-vierkant kiezen, maar het mag ook wel een vijf-bij-zeven-rechthoek zijn. Maak het speelveld niet te klein als je jezelf de kans wilt gunnen om de aardige kanten van het spel te ervaren. In de figuren bij dit artikel hebben we een vier-bij-vier-veld gekozen omdat dat gemakkehjk is voor het uitleggen. Je kunt je speelveld gemakkelijk tekenen op roosterpapier (schaf er maar een flinke voorraad van aan, dat zal je wel nodig hebben, omdat het spel je niet zal loslaten). De twee spelers zetten om de beurt. Elke zet bestaat uit het plaatsen van een van de volgende tekeningetjes in een van de vierkantjes van het speelveld.

De eerste speler heeft echter geen vrije keuze: hij moet een kruis zetten in het vierkantje in de linkerbovenhoek van het speelveld. De tweede speler kiest een van de „poten" van dat kruis en,,verlengt" die door zijn` zet. Zo ontstaat een ,,pad" dat bij elke volgende zet opnieuw verlengd moet worden. In de onderstaande figuur is dat duidelijk te zien. Let daarbij vooral ook eens op de toestand, die door de derde zet van B ontstaat. Bij die zet wordt een reeds op het speelveld aanwezig lijntje, dat niet tot het pad behoorde, in het pad opgenomen.

Bij het bestuderen van deze figuur zal je merken, dat beide spelers angstvallig vermijden het pad dood te laten lopen op de rand van het speelveld. De speler, die door zijn zet het pad de rand van het veld laat bereiken, verliest namelijk (in de figuur verliest B bij zijn vijfde zet), tenzij ... het pad de rand bereikt in het grijze vakje rechtsonder; in dat geval wint hij namelijk. Ziezo, dat zijn de spelregels. En nu maar aan de slag.

De strategie

De geniale vondst van Elwyn R. Berlekamp verschaft de speler, die de eerste zet doet, een tot winst voerende strategie, indien het speelveld een oneven aantal vierkantjes bevat. Bevat het speelveld een even aantal vierkantjes, dan kan volgens Berlekamp echter de tweede speler de winst afdwingen. We bespreken beide gevallen afzonderlijk. Het eerste geval lichten we toe op een vijf-bij-vijf-veld. Nadat B zijn eerste zet gedaan heeft, brengt A in gedachten een verdeling van het speelveld aan in een-bij-twee-rechthoekjes (gemakshalve noemen we ze domino's). Omdat het totale aantal vierkantjes oneven is, moet er bij die verdeling een vierkantje over blijven. Daarvoor kiest A het grijze vakje rechtsonder. Bovendien zorgt hij ervoor, dat zijn eerste zet en die van B samen op een domino liggen.

In de bovenstaande figuur is dit aangeduid door de dikke lijnen. Het zal wel duidelijk zijn, dat zulk een verdefing altijd aan te brengen is, hoe de afmetingen van het speelveld ook zijn mogen.

De eerste zet van B leidt het pad nu naar de rand van een nieuwe domino toe. A moet nu zo zetten, dat hij B dwingt die nieuwe domino vol te maken. Daardoor voert B het pad weer naar de rand van een derde domino, die A weer zodanig begint te vullen, dat B hem verder moet vol maken, enzovoorts.

Tenslotte zal B het pad moeten voeren naar de rand van het speelveld, eventueel naar de rand van het grijze vakje. In beide situaties wint A.
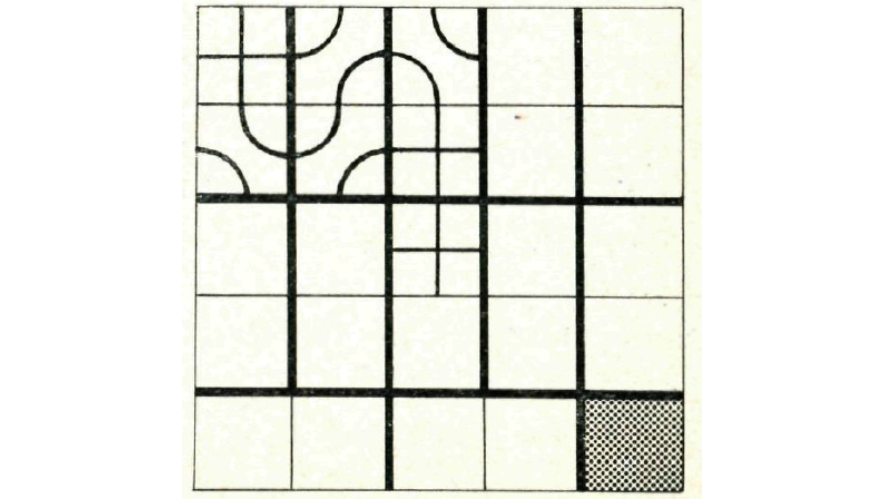
Bij een even aantal vierkantjes kan B zich zeker stellen van winst. We geven hieronder aan, hoe hij moet handelen. Dit lichten we toe op een vier-bij-vier-veld. Evenals A in het bovenstaande geval, moet ook B weer met domino's gaan werken. Nu zou je misschien denken, dat B het speelveld zodanig bedekt denkt met domino's dat alleen het startvierkantje linksboven en het grijze vierkantje rechtsonder niet tot een domino behoren. Dat is echter onmogelijk; we zullen dat eerst bewijzen. Denk je daartoe het speelveld gekleurd zoals een schaakbord of een dambord dat is, met afwisselend zwarte en witte velden. Het startvierkantje en het grijze vierkantje zijn dan aUebei zwart of aUebei wit. Bij de resterende vierkantjes zijn er dus of meer witte of meer zwarte En omdat een aantal domino's altijd evenveel witte als zwarte velden bedekken, kunnen die resterende velden niet met domino's bedekt worden. Hoe je het ook probeert, er blijven altijd twee velden over, die beide zwart of beide wit zijn. Berlekamp noemt die twee overblijvende velden een ,,gespleten domino".

Op de openingszet van A antwoordt B nu zoals in de figuren 4a, 4b en 4c getoond wordt. Daardoor moet A gaan zetten op het vierkantje, dat schuin naast het startveld ligt. Hij kan dat op drie manieren doen, die alle drie afgebeeld zijn.
B wacht dat antwoord van A af en let daarbij in het bijzonder op het lijntje van die zet van A, dat niet tot het pad behoort. Dat lijntje verbindt twee vierkantjes, die dezelfde kleur zouden hebben als het speelveld er als een schaakbord uitzag. Die twee velden beschouwt B nu als samen de ,,gespleten domino" vormend. Je zou kunnen zeggen, dat A met zijn zet zijn doodvonnis getekend heeft. Want nu B de gespleten domino gekozen heeft, verdeelt hij de rest van het speelveld in domino's op een verder volkomen willekeurige manier (het lukt altijd). En daarna wint hij op dezelfde manier als A dat in het vorige geval deed: door A te dwingen telkens een domino vol te maken.