
Het getal 60
Toen Pythagoras $50$ jaar bestond vroeg de redactie van Pythagoras aan de getaltheoreticus Hendrik Lenstra om een artikel te schrijven over het getal $50$. Hendrik reageerde op deze vraag: "Nee, dat artikel kan ik niet schrijven, want $50$ is een compleet oninteressant getal."
Verderop in deze Pythagoras wordt bewezen dat oninteressante getallen niet bestaan. Je kunt, nadat onze redacteur Matthijs Coster een paar bijzonderheden van het getal $60$ heeft opgesomd, zelf oordelen hoe interessant je $60$ vindt.
- De kleinste simpele niet-abelse groep bevat zestig elementen. Dat valt hier niet in het kort uit te leggen.
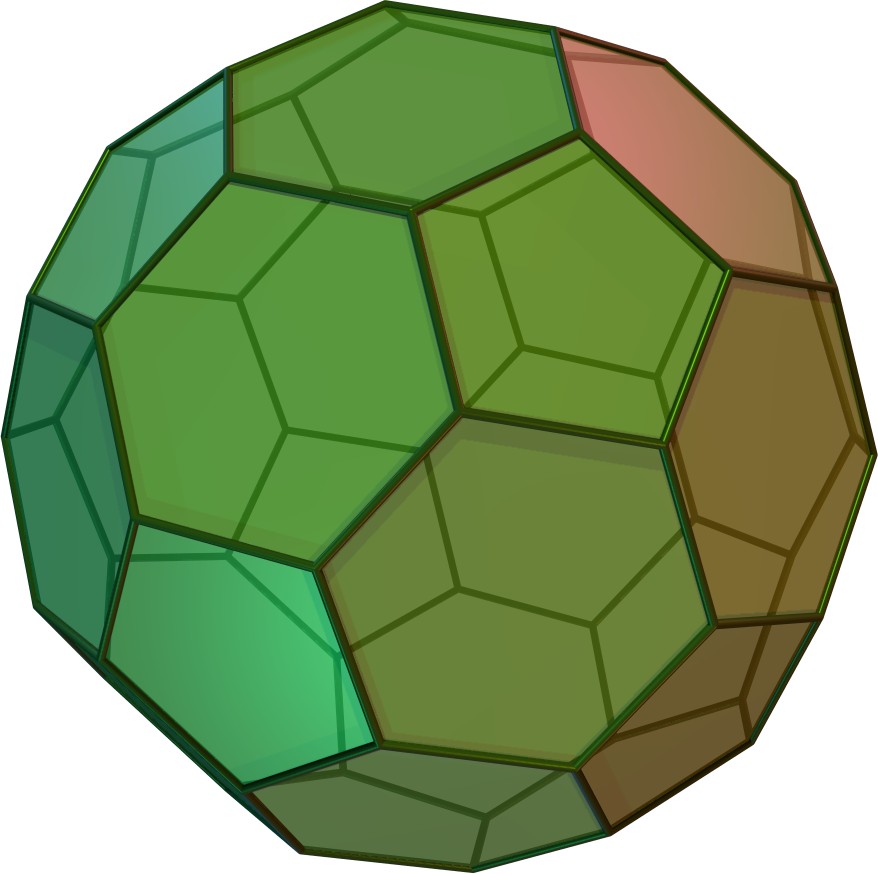
- De icosaëder (het regelmatig twintigvlak) is één van de vijf platonische lichamen. Voor de platonische lichamen wordt één vaste lengte als ribbe gebruikt. Daarmee worden regelmatige veelhoeken gemaakt. In het geval van de icosaëder zijn dat 20 (gelijkzijdige) driehoeken. De afgeknotte icosaëder kun je verkrijgen door alle hoekpunten van de icosaëder iets af te vlakken, (hier ontstaan regelmatige vijfhoeken) en zodat er regelmatige zeshoeken resteren (van de gelijkzijdige driehoeken). Het aantal hoekpunten is zestig. De afgeknotte icosaëder is ook bekend als de Buckminsterfullereen en wordt genoteerd met C60 (inderdaad op elk van de hoekpunten kan een koolstofatoom worden geplaatst). De afgeknotte icosaëder is ook bekend van de voetbal. Zie figuur 1.
- Op een vergelijkbare manier als de afgeknotte icosaëder kan ook de rhombicosidodecahedron worden gecreëerd met zestig hoekpunten. Zie figuur 2.
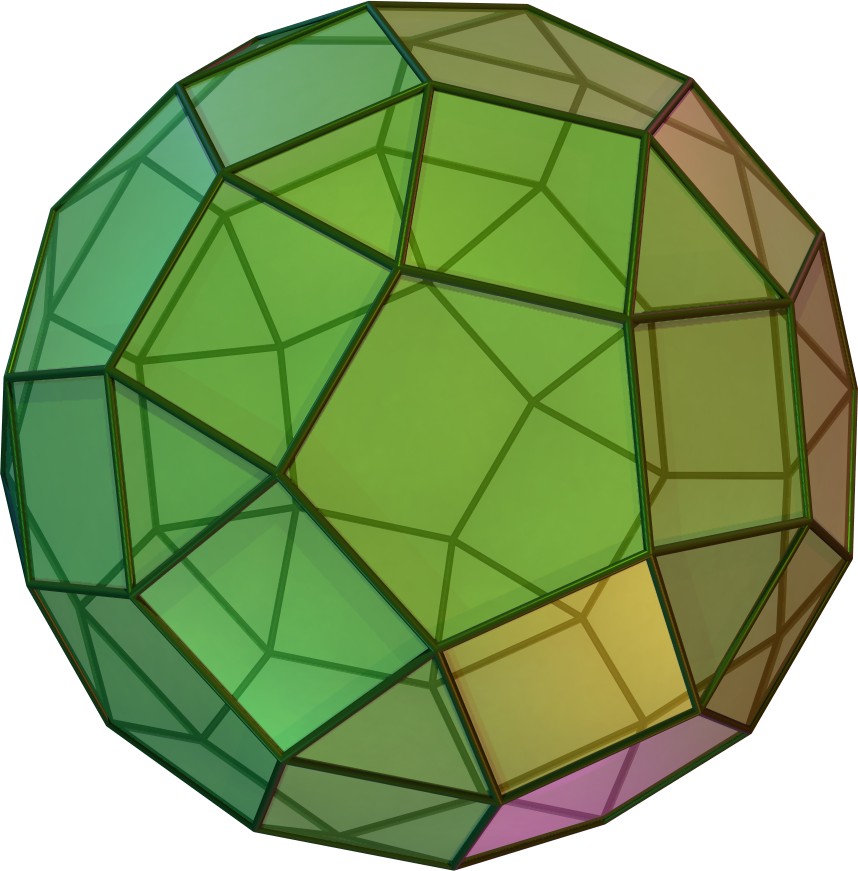
Figuur 2 - Rombische icosidodecaëder
En verder:
$60$ is het product van drie opeenvolgende getallen.
$60$ is de som van 3, 5 en 8 opeenvolgende (positieve) getallen.
$60$ ligt te midden van een priemtweeling.
$60$ is de som van een priemtweeling.
$60$ is de som van 4 opeenvolgende priemgetallen.
. . . en nog veel meer.
