Dit stond onderaan een berichtje dat ik kreeg. Er is inderdaad wel iets fascinerends aan het geheel van eigenschappen die werden opgesomd in het berichtje:

	$2025$	$=$	$45^2$
	$2025$	$=$	$9^2\times5^2$
	$2025$	$=$	$3^4\times5^2$
	$2025$	$=$	$40^2+20^2+5^2$
	$2025$	$=$	$1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3$

Als je weet dat $2025 = 45^2$, dan zijn de tweede en derde regels van dit rijtje niet echt verrassend. De derde regel was volgens het berichtje bijzonder omdat $2025$ hiermee een ontbinding in priemfactoren heeft die de getallen $2, 3, 4$ en $5$ bevat. En dat is best mooi. Veel andere getallen met deze eigenschap zijn er niet. Als je even nadenkt realiseer je je dat $4$ altijd een exponent moet zijn en kun je het hele rijtje opschrijven:

	$2^4\cdot3\cdot5$	$=$	$240$
	$2\cdot3^4\cdot5$	$=$	$810$
	$2\cdot3\cdot5^4$	$=$	$3750$
	$2^4\cdot5^3$	$=$	$2000$
	$2^3\cdot5^4$	$=$	$5000$
	$2^5\cdot3^4$	$=$	$2592$
	$2^4\cdot3^5$	$=$	$3888$
	$3^2\cdot5^4$	$=$	$5625$
	$3^4\cdot5^2$	$=$	$2025$

In $2000$ was de mensheid veel te druk met het millennium en bovendien bestonden er toen nog geen smartphones, dus gingen dit soort berichtjes niet zo gemakkelijk de wereld rond. Ik denk dat ik niet de enige ben die nu pas ziet dat $2000$ niet alleen in de verzameling duizendvouden maar ook in dit rijtje voorkomt. Of die voor het eerst over het rijtje van alle getallen met een priemontbinding die de getallen $2, 3, 4$ en $5$ bevat nadenkt. Wie weet zullen er rond de eeuwwisseling naar $2592$ weer mensen zijn die zich hierover buigen.

Hoe vaak is een jaartal een kwadraat

Lang geleden, aan het begin van onze jaartelling, maakte de gemiddelde mens meerdere 'kwadraatjaren' mee in zijn leven, zelfs al werden de mensen niet zo oud. De eerste kwadraten liggen immers dicht bij elkaar. Maar al in de vijfde eeuw werd de spoeling dunner: alleen $441 = 21^2$ en $484 = 22^2$ waren kwadraatjaren. In de tiende eeuw kwam maar één kwadratisch jaar voor: $961 = 31^2$; in de elfde eeuw waren er weer twee: $1089 = 33^2$ en $1024 = 32^2$ (en $1024 = 2^{10}$ is in een stukje over al dan niet bijzondere getaleigenschappen vast ook de moeite van het noemen waard). Sinds de zestiende eeuw heeft iedere eeuw slechts één kwadraatjaar gekend. De 25^e eeuw zal er weer twee hebben: $2401 = 49^2$ en $2500 = 50^2$. Daarna komt dan de 26^e eeuw waarin men het zonder kwadraatjaar zal moeten doen.

Hoe zit dat eigenlijk met de afstand tussen kwadraten? Als je vaak grafieken van parabolen hebt moeten tekenen op ruitjespapier, heb je wellicht een patroon herkend: "Eén hokje naar rechts, één naar boven, eentje naar rechts, drie naar boven, eentje naar rechts, vijf naar boven, etc." Dat patroon $1, 3, 5, 7, 9, \dots$ heeft alles te maken met de afstand tussen kwadraten. Immers, $1^2 = 1$, vervolgens moet je drie naar boven om in $2^2 = 4$ te komen, en dan vijf naar boven voor $3^2 = 9$ en zeven naar boven voor $4^2 = 16$. Anders geformuleerd:

	$2^2-1^2=3$	$3^2-2^2=5$
	$4^2-3^2=7$	$5^2-4^2=9$

Opgave 1 Wat merk je op aan de getallen hierboven? Wat is de relatie tussen de verschillen en de getallen die je kwadrateert en van elkaar aftrekt?

Deze relatie kun je ook heel gemakkelijk algemeen aantonen. Neem een willekeurig kwadraat en noem het $n^2$, waarbij $n$ een positief geheel getal is. Het volgende kwadraat is dan $(n + 1)^2$. Netjes wegwerken van de haakjes geeft:

$(n + 1)^2 - n^2 = n^2 + 2n + 1 - n^2 = 2n + 1$.

En een stapje verder denken geeft het resultaat dat je hierboven waarschijnlijk gevonden hebt, maar nu in algemene vorm: 

$(n+1)^2-n^2=(n+1)+n$.

Dit geeft je een makkelijke manier om een volgend of vorig kwadraat te vinden. Bijvoorbeeld, $21^2 - 20^2 = 21 + 20$, dus $21^2 = 20^2 + 20 + 21 = 400 + 20 + 21 = 441$. Of $46^2 - 45^2 = 46 + 45$, dus $46^2 = 45^2 + 45 + 46$.

Opgave 2 Wetende dat $45^2 = 2025$, gebruik dit om het volgende kwadraatjaar te berekenen. Vind op eenzelfde manier het vorige kwadraatjaar.

Een som van drie kwadraten

De volgende eigenschap, "2025 kan worden geschreven als de som van drie kwadraten", lijkt nog bijzonderder. Maar dat is hij niet. Dit heeft te maken met de Drie-kwadratenstelling van Legendre. Deze stelling zegt dat een positief geheel getal $n$ kan worden geschreven als $n = x^2 + y^2 + z^2$, tenzij $n = 4^a(8b + 7)$ voor niet-negatieve gehele getallen $a$ en $b$.

De eerste getallen die je kunt schrijven als $n = 4^a(8b + 7)$, en dus niet als de som van drie kwadraten, zijn:

$7, 15, 23, 28, 31, 39, 47, 55, 60, 63, 71$.

Sinds het jaar 2000 kon je alleen de jaren 2007, 2012, 2015 en 2023 niet schrijven als de som van drie kwadraten. Vorig jaar was bijvoorbeeld $2024 = 2^2 + 16^2 + 42^2$ en volgend jaar is, niet geheel verrassend, te schrijven als $2026 = 0^2 + 1^2 + 45^2$. Het eerstvolgende jaar dat je niet op deze manier kunt schrijven is 2031, en dan volgt meteen 2032. Ook zo'n opeenvolgend stel van jaren dat je niet als de som van drie kwadraten kunt schrijven is niet bijzonder. Ivan Neretin bewees in 2017 dat er oneindig veel van dergelijke paren zijn, bijvoorbeeld $128k + 111$ en $128k + 112$ voor ieder willekeurig geheel getal k, maar dat er geen drietallen bestaan.

Een eigenschap die ontbrak in het lijstje bovenaan, is het feit dat 2025, net als ieder kwadraat, kan worden geschreven als de som van twee opeenvolgende driehoeksgetallen. Dat zijn getallen die je krijgt als je met behulp van punten een gelijkzijdige driehoek tekent, zie de figuur. Even slim rekenen levert een standaardformule voor deze getallen.

Opgave 3 Wat merk je op aan de getallen hierboven? Wat is de relatie tussen de verschillen en de getallen die je kwadrateert en van elkaar aftrekt?

De algemene uitdrukking voor het $n$^e driehoeksgetal is $T_n = \tfrac{1}{2}n (n + 1)$. Als je nu twee opeenvolgende driehoeksgetallen optelt, krijg je m.b.v. haakjes wegwerken, vereenvoudigen en vervolgens ontbinden in factoren: 

$T_n+T_{n+1}$	$=$	$\tfrac{1}{2}(n+1)+\tfrac{1}{2}(n+1)(n+2)$
	$=$	$(n+1)\left(\tfrac{1}{2}n+\tfrac{1}{2}(n+2)\right)$
	$=$	$(n+1)(n+1)=(n+1)^2$

Voor $n = 44$ geeft dit dat $2025 = T_{44} + T_{45}$.

Een som van derdemaChten

De laatste eigenschap in het lijstje is dat 2025 kan worden geschreven als de som van opeenvolgende derdemachten. Dit is een voorbeeld van een formule die in Pythagoras 57-5/6 werd getoond als Een oud bewijs zonder woorden: 

$(1 + 2 + 3 + \dots + n)^2 = 1^3 + 2^3 + 3^3 + \dots + n^3$.

Omdat $1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45$ geeft dit $2025 = 45^2 = 1^3 + 2^3 + 3^3 + \dots + 9^3$. Het vorige jaartal dat op deze manier kan worden geschreven kun je vinden met $n = 8$, dat was het jaar $1296$. En op het volgende moeten we precies $1000$ jaar wachten.

(Waarom?)

De uitsmijters

Je kunt $2025 = 45^2$ ook nog schrijven als $2025 = (20 + 25)^2$. Visueel aantrekkelijk en bijzonder. Om jaartallen te vinden waarvoor net zoiets geldt, moet je zoeken naar positieve, gehele getallen $a$ en $b$ waarvoor $100a + b = (a + b)^2$. Er zijn twee simpele oplossingen: $(a, b) = (0, 1)$ en $(a, b) = (100,0)$, corresponderend met de jaartallen $1$ en $10\,000$. Verder zijn er nog maar twee oplossingen: $(a, b) = (30, 25)$ en $(a, b) = (98, 1)$. Ofwel, $3025 = (30 + 25)^2$ en $9801 = (98 + 01)^2$.

Paul Levrie kwam met een nog specialere eigenschap. Hij merkte het volgende op: als je $1$ optelt bij ieder cijfer in de gelijkheid $2025 = 45^2$, krijg je weer een gelijkheid die klopt:

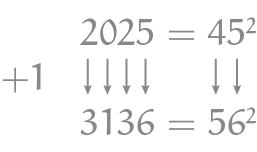
De vorige keer dat zoiets waar was, was in het jaar $25$. En aangezien de vergelijking $x^2 + 1111 = (x + 11)^2$ het getal $45$ als enige oplossing heeft, gaan we voor het jaar $10\,000$ geen jaartal meer krijgen waarvoor zoiets waar zal zijn. Al met al is 2025 dus best een bijzonder jaartal!