Het SOS-spel: analyse
[oOO]
De familie Van der Torus is een heel normale, gemiddelde familie. Voor zover een familie van wiskundigen normaal kan zijn. Ze komen allerlei alledaagse problemen tegen. Kom je zelf uit een wiskundig gezin of ben je een (mogelijk toekomstige) wiskundige, dan kun je je ervaringen, vragen en ideeën delen met de familie Van der Torus via email naar [email protected].
Sinds ze het SOS-spel leerden, spelen Milli en Mu bijna dagelijks een potje. Meestal de variant waarbij je begint met een rij lege hokjes waarin je vervolgens om de beurt een letter $S$ of $O$ zet en wint als je als eerste SOS maakt. Tijdens een van die potjes doen ze opeens een ontdekking. Heb jij ook lekker gespeeld en wat ontdekt?
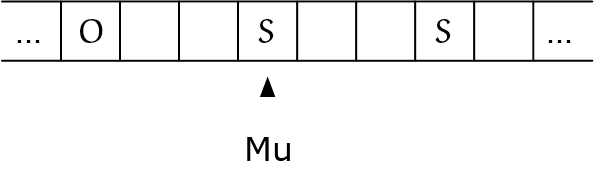
Na een paar zetten is Mu aan de beurt en schrijft een $S$ op (figuur 1). Daarbij ontstaat het patroon $S\ \_\ \_\ S$, dus een $S$, dan twee lege hokjes en daarna nog een $S$. Milli is nu aan de beurt, maar als die een letter op een van deze twee lege hokjes plaatst, gaat Mu winnen. Probeer zelf maar. Als Milli er een $S$ neerzet, dan kan Mu winnen door een $O$ in het andere lege hokje te schrijven. Maar als Milli een $O$ schrijft, dan wint Mu juist door er een $S$ naast te zetten. Met deze kennis kan je anders over het spel denken. Moet je dat patroon nu juist wel maken, of moet je zorgen dat de ander het niet kan maken? Misschien heb je daar zelf ook al over nagedacht.
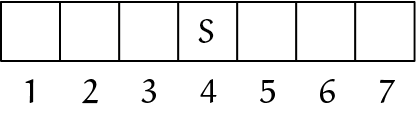
Laten we het aantal lege hokjes waarmee je begint $N$ noemen. We nummeren die hokjes van $1$ tot en met $N$. Milli en Mu hebben ook al ontdekt dat voor $N \le 6$ deze variant van het SOS-spel net zo saai is als boter-kaas-eneieren: geen van beide spelers kan dan winst afdwingen. Met andere woorden, het wordt altijd remise als de spelers geen fouten maken. Bij $N = 4$ moet je bijvoorbeeld niet beginnen met een $S$ op de rand te zetten. De ander zet dan immers een $S$ op de andere rand (figuur 2). We duiden die zetten aan met $S\ 1$ en $S\ 4$.
Voor $N \le 6$, kun je remise afdwingen door een $O$ op de rand te zetten: $O\ 1$ of $O\ N$. Dat komt omdat niemand wat heeft aan een $O$ op de rand.
Vanaf $N = 7$ hokjes wordt dat anders. Voor $N = 7$ is er maar één winnende beginzet. Probeer die eerst zelf te vinden voordat je verder leest.
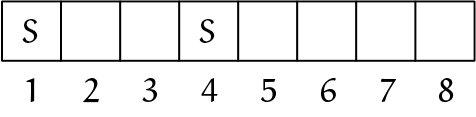
Nu is een $O$ op de rand plaatsen geen goed idee, want dan wordt het remise (bij goed tegenspel) omdat je gewoon de situatie met $6$ lege hokjes creëert. Als je een $S$ in het midden zet ($S\ 4$, figuur 3), dan kan de tegenstander niet voorkomen dat je in je volgende beurt een $S$ op een van de randen kan plaatsen en het patroon $S\ \_\ \_\ S$ maakt.
Bovendien pakt het aantal lege hokjes dat niet tussen die twee $S$-en staat, dan net gunstig uit voor de beginner. Omdat dit aantal even is, wordt de ander uiteindelijk gedwongen om de eerste zet tussen de $S\ \_\ \_\ S$ te doen.
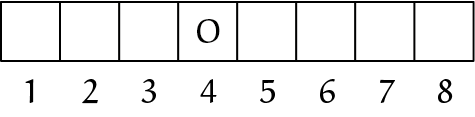
Voor $N = 8$ werkt dit niet. De beginner kan wel het patroon $S\ \_\ \_\ S$ forceren (figuur 4), maar dat pakt dan net slecht uit waardoor het tot verlies leidt. Het beste dat de beginner nu kan doen is remise houden. Maar uiteraard niet door te beginnen met een $O$ op de rand. Een $O$ op een van de twee hokjes in het midden ($O\ 4$ of $O\ 5$, figuur 5) voorkomt dat de tweede speler het patroon $S\ \_\ \_\ S$ kan maken.
Analyse door Pi en Phi
Pi en Phi spelen zelf ook weleens, maar ze zijn te lui om hard na te denken over wat nou de beste beginzet is voor een gegeven aantal lege hokjes bij de start. Ze schreven een computerprogramma dat systematisch alle mogelijkheden afgaat. Het programma probeert elke mogelijke zet voor de beginner en dan elke mogelijke zet voor de tweede speler, etc. en beoordeelt telkens de spelsituatie. Een situatie met daarin SOS is verloren voor de speler die dan aan de beurt is. Als een speler een zet kan doen die de ander een verloren situatie geeft, dan is dat een winnende zet. En als een speler geen winnende zet kan doen, maar wel een zet die niet verliest (dus remise oplevert), dan is dat de beste zet. Als een speler geen zet kan doen om te winnen of remise te houden, dan is het een verloren situatie.
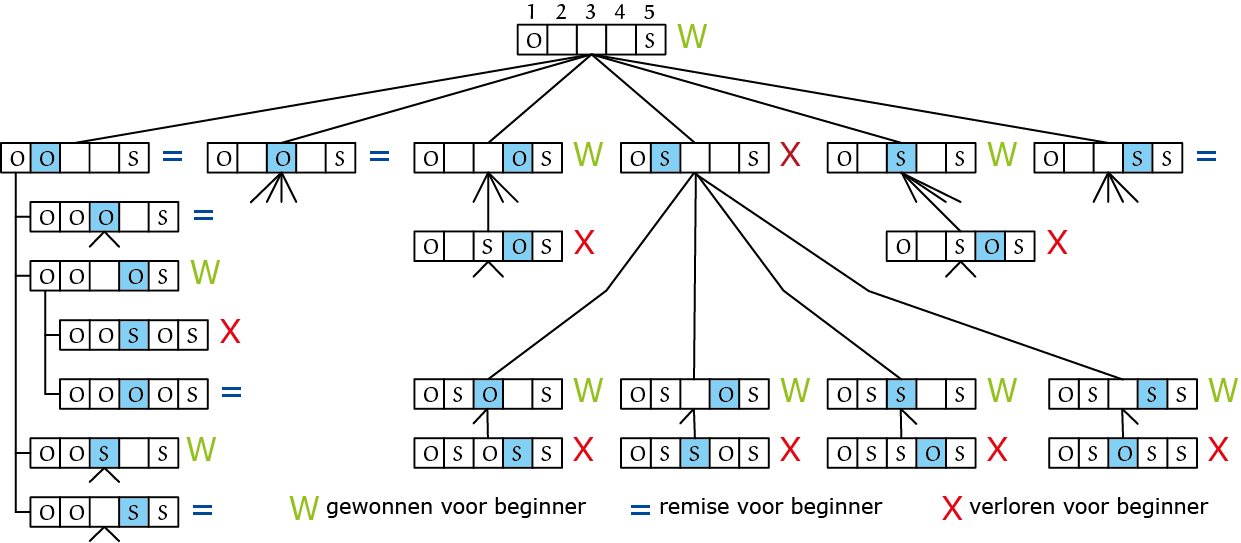
Figuur 6 toont een spelboom voor $N = 5$ vanuit de situatie $O\ \_\ \_\ \_\ S$. Dit is voor de beginner een gewonnen stand, omdat $S\ 2$ tot een verloren stand voor de ander leidt. En waarom is dat een verloren stand? Omdat elke zet van de ander dan tot een gewonnen stand leidt. Zo kun je ook inzien dat de beginzet $O\ 2$ tot remise leidt bij het beste tegenspel, omdat de tegenstander geen winnende zet heeft, maar ook niet hoeft te verliezen. Op deze manier konden Pi en Phi onderstaande tabel maken. Deze tabel toont voor $N = 1$ t/m $16$ de uitslagen (win, remise, verlies) gezien vanuit de beginner, bij het beste spel, alsmede een beste beginzet als de beginner kan winnen of remise houden (soms zijn er meer beste zetten). Snap je waarom de beginner bij $N = 16$ zelfs geen remise kan houden (zie figuur 7)?
| $\color{white}{N}$ | $\color{white}{uitslag}$ | $\color{white}{N}$ | $\color{white}{uitslag}$ | $\color{white}{N}$ | $\color{white}{uitslag}$ | $\color{white}{N}$ | $\color{white}{uitslag}$ |
| $1$ | remise $O\ 1$ | $5$ | remise $O\ 5$ | $9$ | winst $S\ 4$ | $13$ | winst $S\ 1$ |
| $2$ | remise $O\ 2$ | $6$ | remise $O\ 6$ | $10$ | remise $O\ 5$ | $14$ | remise $O\ 7$ |
| $3$ | remise $O\ 3$ | $7$ | winst $S\ 4$ | $11$ | winst $S\ 4$ | $15$ | winst $S\ 1$ |
| $4$ | remise $O\ 4$ | $8$ | remise $O\ 4$ | $12$ | remise $O\ 6$ | $16$ | verlies (!) |
Pi was aanvankelijk verrast dat de afwisseling van winst en remise, die bij $N = 7$ zo mooi begon, opeens bij $N = 16$ doorbroken werd. Phi wees er even later op dat het eigenlijk heel eenvoudig is, hoewel de computer er lang op moest rekenen. Want zodra het patroon $S\ \_\ \_\ S$ op het bord staat kan het spel niet meer in remise eindigen. Immers de enige reden dat er niet in de lege hokjes tussen die twee $S$-en gezet hoeft te worden is als het spel eerder al is beslist. Wie er dan wint hangt af van het aantal andere hokjes dat nog leeg is. Als dat oneven is, dan wint degene die aan zet is en anders verliest die. Ergens anders nogmaals $S\ \_\ \_\ S$ maken helpt niet, want het aantal "speelbare" lege hokjes neemt dan ook met een oneven aantal af. Bij $N = 16$ kan de beginner niet meer voorkomen dat de tweede speler het patroon $S\ \_\ \_\ S$ op het bord krijgt, omdat er na de eerste zet altijd minstens $7$ lege hokjes naast elkaar beschikbaar blijven.
Hoe zit het als je met een rij van $100$ lege hokjes begint? Wil je dan de eerste zet doen of toch liever niet? Bij [Bekijk Oplossing] vind het antwoord. Daar vind je ook (het verrassend korte) Python programma.
