De lijst priemgetallen maken we met behulp van de zeef van Erathostenes. We laten eerst met de rij getallen van $2$ tot en met $16$ zien hoe de zeef werkt.

We beginnen met twee lijsten: de lijst van alle getallen $Z = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]$ en de nu nog lege lijst van priemgetallen $P$.

Een aantal malen herhalen we de volgende stap: neem het kleinste getal uit $Z$. Dit is een priemgetal. Dat voegen we toe aan de lijst $P.$ We krijgen nu $P = [2]$ en $Z = [3, \mathbf{4}, 5, \mathbf{6}, 7, \mathbf{8}, 9, \mathbf{10}, 11, \mathbf{12}, 13, \mathbf{14}, 15, \mathbf{16}]$, waarbij vetgedrukte getallen, de veelvouden van $2,$ zullen worden verwijderd. Zo houden we over:

$$Z = [3, 5, 7, 9, 11, 13, 15].$$

Deze stap herhalen we voor het nu kleinste getal in de verzameling: $3.$ Dit getal voegen we toe aan $P,$ dus $P = [2, 3].$ We verwijderen alle drievouden in $Z.$ $Z = [5, 7, \mathbf{9}, 11, 13, \mathbf{15}].$

Hiermee hebben we $P = [2, 3]$ en $Z = [5, 7, 11, 13].$

In de lijst $Z$ zullen we nu alleen nog maar priemgetallen aantreffen. Het eerste veelvoud van $5$ zou $5^2$ zijn, en dat is te groot. We voegen de twee lijsten samen en zo vinden we de priemgetallen $[2, 3, 5, 7, 11, 13].$

Door te programmeren kunnen we echter veel verder komen.

1. Schrijf alle getallen op van $2$ tot en met $50.$
2. We nemen het eerste getal van de lijst, $2$, en strepen alle veelvouden van $2$ weg. Het getal $2$ bergen we op een in een andere lijst.
3. We nemen het volgende getal in de lijst: dat is $3.$ We strepen alle veelvouden van $3$ door en bewaren $3$ in de andere lijst.
4. We doen hetzelfde met het volgende getal, $5$ en daarna met $7.$

In code ziet het er als volgt uit. (De uitvoer staat onder de code.)

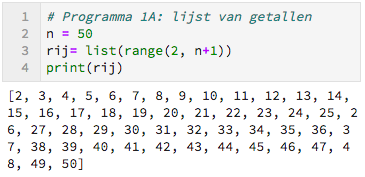
Toelichting: in regel 3 wordt de verzameling van getallen $2 \dots 50$ gegenereerd. Let op range(a,b) loopt van $a$ tot en met $b - 1.$

We halen het nulde (dus voorste) element uit de rij door middel van pop(0) en slaan het op in de variabele pr. Deze variabele voegen we toe aan de lege rij priemrij.

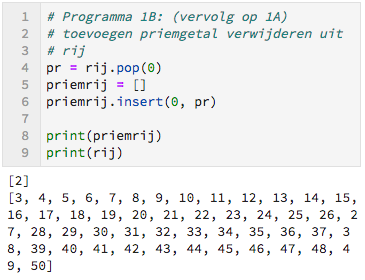
Toelichting: met rij.pop(k) wordt het $k$-de element opgeroepen en uit de list rij verwijderd. Let op dat lijsten in Python genummerd zijn vanaf $0$. Met rij.pop() wordt het laatste element opgeroepen en verwijderd van rij. Hier gebruiken we pr = rij.pop(0). In pr wordt dus de waarde rij.pop(0) geplaatst.

Nu strepen we alle veelvouden van $2$ weg uit de rij.

Toelichting: We maken nu gebruik van remove. Er zijn twee verschillen bij het gebruik van pop en remove:

1. Aan pop geef je de index mee, aan remove geef je de waarde mee die je gaat verwijderen. Met rij.remove[j] verwijder je dat element van rij waar voor de eerste keer de waarde $j$ voorkomt.
2. rij.pop(k) geeft de waarde van rij[k] terug (voordat rij[k] wordt verwijderd). remove(j) geeft geen waarde terug.

Hetzelfde doen we met het getal dat nu voorop in de rij staat.

We doen het nog twee keer, dus met $5$ en met $7.$ We krijgen de twee rijen die we samenvoegen tot één rij.

Als we deze twee rijen samenvoegen, hebben we alle priemgetallen gevonden kleiner of gelijk aan $50.$ Waarom werkt dit algoritme?

De eerste rij bevat het priemgetal $2.$ De overblijvende rij bevat getallen die geen veelvoud zijn van $2.$ Het eerstvolgende getal, $3,$ moet een priemgetal zijn, want het heeft geen kleinere echte delers dan zichzelf. We verwijderen de veelvouden van $3.$ Om dezelfde reden moeten $5$ en $7$ ook priem zijn.

Het volgende getal $11$ is ook priem. We hoeven de lijst echter niet meer na te lopen voor veelvouden van $11,$ want voor elk veelvoud $t \cdot 11$ is $t < 50/11 < 7.$ In feite hoeven we alleen maar veelvouden van priemdelers kleiner dan $\sqrt{50}$ weg te strepen.

We gaan bovenstaand proces automatiseren met een for-loop.

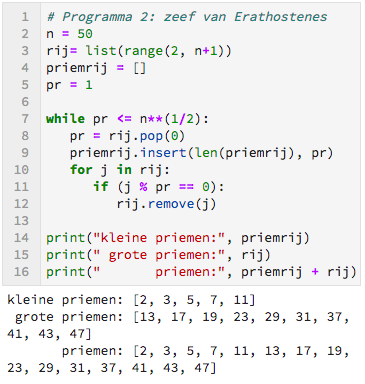
Toelichting op het programma: in regel 7 staat een while-statement. De regels die inspringen onder het while-statement worden uitgevoerd zolang de conditie achter het while-statement waar is. In het algemeen brengt het programmeren met while-statements een gevaar met zich mee, dat het programma oneindig lang blijft draaien.

Het programma heeft twee minder mooie aspecten. Het laatste priemgetal wordt wel bij de priemrij gevoegd, maar niet weggestreept in de lange rij getallen. Bij het samenvoegen van de twee rijen komt het wel precies weer goed.

Het tweede aspect is dat het programma niet werkt voor de twee waarden $n = 2$ en $n = 3.$ Dat is te ondervangen door de priemrij te laten lopen tot $\sqrt{n}+1.$

Het programma kan korter als je het wegstrepen met een zogenaamde inwendige functie doet.

Toelichting: In regel 11 worden de bewerkingen van Programma 2 (regels 10 tot 12 samengevoegd tot één regel. Deze manier om een list te creëren heet een list comprehension. Het staat uitgebreid uitgelegd op bladzijde 163 van de De Programmeursleerling van Pieter Spronck. De opdracht

rij = list(x for x in rij if (x % pr != 0))

betekent: we maken een list door steeds de uitkomst x (de eerste x) toe te voegen, waarbij de variabele x de list rij doorloopt, waarbij we x overslaan als x % pr == 0. Het is een fijne snelle techniek, die je echter niet per se nodig hebt.

Nu staat de weg vrij om willekeurig lange rijen priemgetallen te genereren.

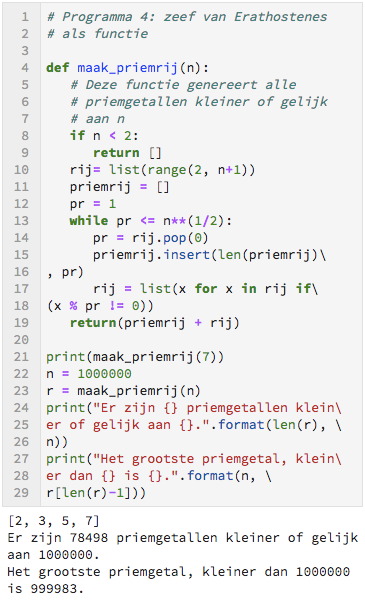
Toelichting: Regel 4 t/m 19 definiëren een functie. In de toekomst zullen we er nog veelvuldig gebruik van maken. In dit geval heet de functie maak_priemrij.

Onze functie krijgt één argument mee: n. We plaatsen onder en boven de functie een witregel. Zo zijn de functies in het programma beter herkenbaar. De regels die volgen zijn herkenbaar uit Programma 3, en springen in, net zoals we eerder hebben gezien met for-loop en if-statement.

Regel 8 en 9 zijn toegevoegd om te voorkomen dat iemand een priemrij voor $0$ of $1$ gaat uitrekenen. In regel 21 en 23 wordt de functie aangeroepen.

In regel 21 wordt de complete rij priemgetallen geprint tot en met getal $7.$ Dat is wel doenlijk. Dat is voor n = 100000 (regel 22) af te raden. Daarvoor in de plaats worden het aantal priemgetallen en het grootste priemgetal getoond.

We zien in regels 24 t/m 29 tevens hoe je efficiënt kunt printen. Op de plekken waar je in de string {} plaatst, wordt automatisch de corresponderende waarde gehaald uit het format. Er staat hetzelfde als print("Er zijn", len(r), "priemgetallen kleiner of gelijk aan", n,."."). Later zullen we toepassingen zien waarbij de printopdracht uit regels 24 en verder veel beter werkt dan die hierboven is beschreven.

We hebben dus uitgerekend dat er iets meer dan $78 000$ priemgetallen zijn onder het miljoen. Het grootste priemgetal onder het miljoen is $999 983.$

Priemgetallen met Euclides

Er zijn oneindig veel priemgetallen. Een bewijs daarvoor komt voor in De elementen van Euclides. Het bewijs geeft een constructiemethode voor nieuwe priemgetallen. We laten eerst die constructie zien en zullen daarna proberen er nieuwe priemgetallen mee te genereren met de constructie van het bewijs. Er komen interessante vragen naar voren.

Het idee achter de constructie van steeds weer nieuwe priemgetallen gaat als volgt. We gaan uit van een aantal priemgetallen, bijvoorbeeld $2, 5$ en $11.$ We vermenigvuldigen ze met elkaar en tellen er $1$ bij op. We krijgen $2 \cdot 5 \cdot 11 + 1 = 111.$ Het getal $111$ is niet deelbaar door $2,$ niet door $5$ en niet door $11,$ want bij deling houden we steeds rest $1$ over. Het getal $111$ moet dus deelbaar zijn door een ander priemgetal. Hier zijn dat $3$ en $37.$

Het factoriseren van getallen kan voor een computer een tijdrovende klus zijn. Voor kleinere getallen draait een computer zijn hand niet om. De computer kan gewoon alle priemgetallen proberen kleiner dan $\sqrt{111}.$ Een functie die een lijst van priemgetallen genereert hebben we in de vorige paragraaf laten zien.

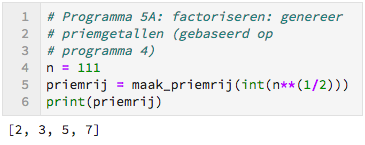
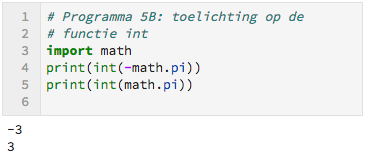
De functie maak_priemrij heeft als invoer een geheel getal, dus converteren we het kommagetal n**(1/2) naar een gehele waarde. De functie int(n) maakt van het kommagetal $n$ een geheel getal door het deel achter de komma weg te laten.

We zoeken de kleinste deler van $111$ en zoeken daarna weer de kleinste deler, totdat we het getal hebben gefactoriseerd. We weten voor $111$ dat we het zoeken van de kleinste deler tweemaal moeten uitvoeren. Daarom staat het for-statement tweemaal onder elkaar.

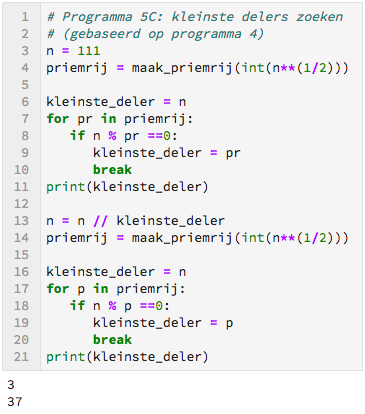
Toelichting: In regel 7 wordt een for-statement aangeroepen. In principe worden de regels die eronder inspringen uitgevoerd voor alle priemen in priemrij. Echter door gebruik te maken van break in regel 10 kan uit de for-loop gesprongen worden. De resterende priemen worden overgeslagen. Het programma is ontworpen om alle factoren $(2)$ van $111$ te vinden. Aangezien je van te voren niet weet om hoeveel factoren het gaat, moeten we daarvoor nog iets bedenken.

Dit algoritme kunnen we in een functie samenvatten.

Zoals je ziet berekenen we de priemrij elke keer opnieuw. Dit houdt de functie eenvoudig, met slechts een argument. Als je echter veel gaat rekenen met grote getallen is het veel sneller om één keer een hele lange priemlijst te maken en deze ook mee te geven aan de functie bepaal_kleinste_deler.

De functie bepaal_kleinste_deler gaan we een aantal keren aanroepen totdat we alle priemdelers hebben gevonden van het getal $n$. Dit gaat weer heel goed door gebruik te maken van een while-statement.

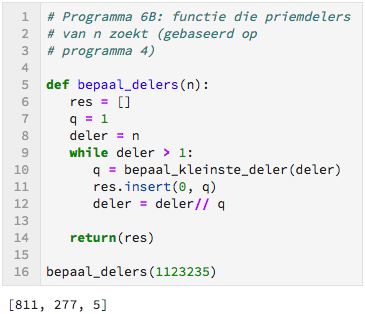
Ter controle berekenen we $811 \cdot 277 \cdot 5.$ Het klopt!

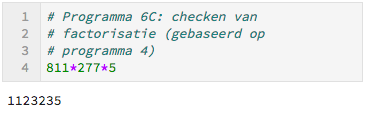
Rijen priemgetallen maken

Nu gaan we met dit Euclidisch algoritme rijen priemgetallen genereren. We starten eerst met het priemgetal $2.$ Het volgende priemgetal wordt $2 + 1 = 3.$ Daarna komt $2 \cdot 3 + 1 = 7$ en daarna $2 \cdot 3 \cdot 7 + 1 = 43.$

Hierna wordt het moeilijk uit je hoofd.

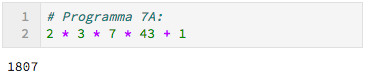
Zou 1807 priem zijn?

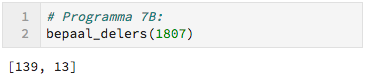
Nee, maar we vinden er wel twee nieuwe priemgetallen bij! We kunnen ze allebei, of één voor één gebruiken om weer een nieuw priemgetal te vinden. We hebben inmiddels de priemgetallen

$$2, 3, 7, 13, 43, 139.$$

Zou je alle priemgetallen op deze manier kunnen krijgen?

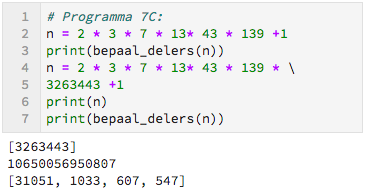
We hebben nu een aantal experimentele onderzoeksvragen.

1. Welk priemgetal kleiner dan $100$ genereert meteen de meeste priemgetallen achter elkaar? Bijvoorbeeld: het priemgetal $2$ genereert de $4$ priemgetallen $2, 3, 7$ en $43,$ daarna volgt $1807$ en dat is samengesteld. Maak hier een grafiek van.
2. Elk oneven priemgetal genereert eerst het priemgetal $2.$ Hoeveel stappen is het voor de priemgetallen onder de $100$ om voor het eerst $3$ te genereren?
3. Je kan het algoritme om nieuwe priemgetallen te maken ook anders aanpakken. Stel je hebt de priemgetallen $2, 3$ en $5.$ Dan hebben we
              $$2^n3^m5^t + 1\mbox{ en }2^n3^m5^t - 1,$$
   met $m, n, t \ge 0$ andere priemfactoren dan $2, 3$ en $5.$
   Hoeveel opeenvolgende priemgetallen kan ik achter elkaar genereren, uitgaande van deze drie priemgetallen? Uitgaande van $2, 3$ en $5$ vind je: $7 = 2 \times 3 + 1,$ $11 = 2 \times 5 + 1,$ $13 = 2^2 \times 3 + 1,$ $17 = 2^4 + 1$ enzovoort.
4. Zoek uit hoe lang het duurt om $P(n) + 1$ te factoriseren, waarbij $P(n)$ het product van de eerste $n$ priemgetallen is. Maak een grafiek van deze tijden en maak vervolgens een schatting op grond van de grafiek welke $P(n)$ je computer nog binnen een dag kan factoriseren (gebruik makende van bovenstaande functies).

Bestaande bibliotheken voor priemgetallen en factoriseren

Nu je de smaak te pakken hebt wil je natuurlijk van allerlei getallen nagaan of het priemgetallen zijn en zo niet dan wil je de getallen kunnen factoriseren. De hierboven beschreven programma's zijn vrij traag. We doen graag een beroep op de modulen math en sympy om daarmee snellere functies te kunnen gebruiken, zodat je de functies ook op grotere getallen kunt toepassen.

Priemgetallen genereren

We behandelen eerst een aantal functies om priemgetallen te genereren.

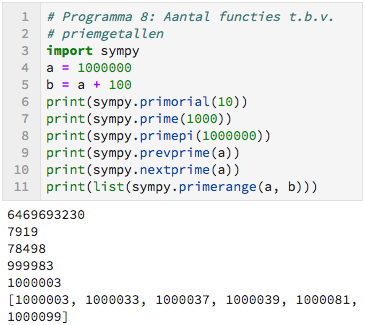
SymPy is een zeer uitgebreide getaltheoretische bibliotheek. Hieronder een beschrijving van de functies die hier worden gebruikt:

• primorial(n) is het product van de eerste $n$ priemgetallen (zie opdracht hier direct boven);
• prime(n): bepaalt het $n^\mbox{e}$ priemgetal;
• primepi(n): bepaalt het aantal priemgetallen, kleiner of gelijk $n;$
• prevprime(n): bepaalt het grootste priemgetal kleiner dan $n;$
• nextprime(n): bepaalt het kleinste priemgetal groter dan $n;$
• isprime(n): gaat na of $n$ een priemgetal is;
• primerange(a, b): maakt een lijst van alle priemgetallen tussen $a$ en $b - 1.$

(Kijk op de site van SymPy voor een volledige toelichting.)

Factoriseren en delers van een getal

Het factoriseren kan ook veel sneller worden uitgevoerd dan met ons programma hierboven. Maak opnieuw gebruik van de bibliotheek sympy.

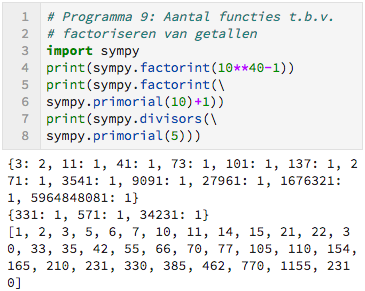
De gebruikte functies zijn:

• factorint(n): bepaalt de factorisatie van $n;$
• divisors(n): bepaalt een lijst met alle delers van $n.$

Beantwoord onderzoeksvraag 4 opnieuw met behulp van deze functies.

Wij zijn heel benieuwd of je zelf ook ideeën hebt om met de priemgetallen en het factoriseren een programma te schrijven. Laat het ons weten op het emailadres [email protected].

Bron:

Pieter Spronck, De programmeursleerling, spronck.net/pythonbook/

Voor de code behorende bij dit artikel kun je op de knop "Bekijk oplossing" hieronder klikken. 

Bekijk oplossing