Bij natuurkunde ben je ‘lenzenformule’ misschien al eens tegengekomen. Deze formule, uit de geometrische optica, beschrijft het verband tussen de voorwerpafstand ($v$), de beeldafstand ($b$) en de brandpuntafstand ($f$) van een lens. De formule luidt: $$\frac{1}{f}=\frac{1}{v}+\frac{1}{b}.$$

De formule geldt voor een ideale dunne lens. Er bestaat trouwens ook nog een overeenkomstige ‘lenzenmakersformule’: $$\frac{1}{f}\approx(n-1)\left(\frac{1}{R_1}+\frac{1}{R_2}\right).$$

Hiermee hielden zeventiende-eeuwse wetenschappers als Spinoza en Christiaan Huygens zich al bezig, om een dunne lens met kromtestralen $R_1$ en $R_2$ goed te slijpen. Maar in dit stuk beperken we ons tot de genoemde lenzenformule.

Hoe kan je die formule goed begrijpen? Hij is niet zo simpel te doorzien. Wordt bij een bepaalde lens $b$ nou groter of kleiner als $v$ groter wordt? Tot overmaat van ramp kunnen zowel $f$ als $b$ ook nog eens negatieve waarden aannemen.

Een afleiding van de lenzenformule staat in het kader hieronder. Maar in dit artikel gaat het niet zo zeer om die afleiding. Het doel is vooral om te begrijpen hoe $v$ en $b$ van elkaar afhangen.

Vaak wordt de lenzenformule ontdekt aan de hand van een practicum. Dan bepaal je een aantal waarden voor $v$ en $b$, en schrijf je die in een tabel. Daarna bereken je de waarden van $1/v$ en $1/b$. Hiervan kan je de gemiddelde waarde berekenen en deze omkeren. Uiteindelijk heb je dan heb je de brandpuntafstand $f$. Inzichtelijk is deze methode niet en bovendien is het maar te hopen dat het een goede benadering van $f$ oplevert. Kan het beter?

Met een grafiek

Stel dat een meting met een gegeven lens de volgende waarden voor $v$ en $b$ geeft:

$v$ (in cm)	$b$ (in cm)
15	48,0
20	29,4
25	20,0
30	18,0
35	16,0

 

Wij gaan $v$ en $b$ niet in een grafiek zetten, maar op de assen als punten $(v,0)$ en $(0,b)$. Vervolgens verbinden we de overeenkomstige punten met rechte lijnen. Er ontstaat dan een lijnenwaaier met een (in de praktijk) bij benadering gemeenschappelijk snijpunt, zie de figuur. Het gemeenschappelijke snijpunt geeft de coördinaten $(f,f)$, waarbij $f$ de brandpuntafstand is.

Waarom is dit zo? De verbindingslijn tussen $(v,0)$ en $(0,b)$ heeft de vergelijking $$y=-\left(\frac{b}{v}\right)x+b,$$ wat mooier te schrijven is als $$\frac{x}{v}+\frac{y}{b}=1.$$          

Als het punt waarvoor geldt dat $x=y=f$  (het punt $(f,f)$ dus) op alle lijnen ligt, dan voldoet $f$ aan de lenzenformule!

Wiskundig kan je een optimale oplossing voor zo’n snijpunt van lijnen vinden door de som van de loodrechte afstanden van dat snijpunt tot elk van de lijnen te minimaliseren. Dit wordt de methode van kleinste kwadraten genoemd. Het lijkt niet erg noodzakelijk, het is op het oog al goed te zien!

De snelle en nauwkeurige bepaling van de brandpuntafstand is de eerste winst. Zijn er nog meer voordelen van deze aanpak? Jazeker.

Ten eerste is te zien dat bij kleinere $v$ een grotere $b$ hoort, en omgekeerd. Ten tweede: voor $v=f$ is er geen snijpunt met de $b$-as, dus ook geen beeld. Ten derde: als $v<f$, dan ligt het snijpunt van de lijn door $(f,f)$ en $(v,0)$ op de negatieve $b$-as: kennelijk is er dan alleen een virtueel beeld mogelijk! En last but not least: de (absolute waarde van de) helling van de verbindingslijnen is gelijk aan $b/v$, oftewel de vergroting van de lens. Hoe steiler de lijn (dat wil zeggen hoe dichter $(v,0)$ het punt $(f,0)$ nadert), hoe groter de vergroting door de lens. Dat is helemaal in overeenstemming met wat we van een lens verwachten!

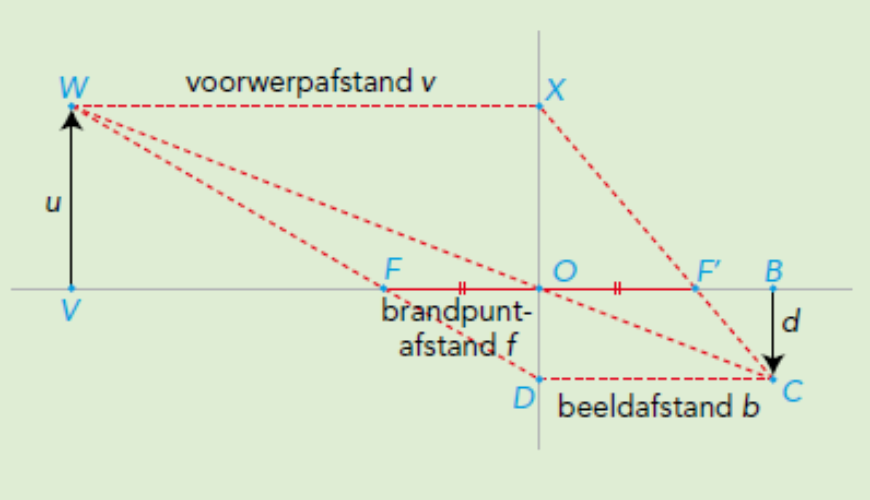
De lenzenformule voor een bolle lens Door het midden van een lens gaat een symmetrie-as. Lichtstralen die evenwijdig aan deze as de bolle lens binnenvallen, komen samen in een punt. Dit punt heet het brandpunt van de lens. In de illustratie is dit punt te vinden met de letter $F'$ van focus. Lichtstralen die evenwijdig de lens verlaten, komen allemaal uit het brandpunt aan de andere kant in de figuur. Dit punt is aangegeven met $F$. Beide punten hebben dezelfde afstand tot de oorsprong: $OF=OF'$. Op grond van de evenwijdigheid van de lichtstralen is $\angle WXD=\angle FOD$ en $\angle CDX=\angle F'OX$. Daarom zijn de driehoeken $WXD$ en $FOD$ gelijkvormig, evenals de driehoeken $CDX$ en $F'OX$. Voor de voorwerpafstand $v=WX$, de beeldafstand $b=DC$, de brandpuntafstand $f=OF=OF'$, $u=WV=XO$ en $d=CB=DO$ volgen de twee gelijkheden $$\frac{u}{v}=\frac{d}{b}$$ en $$\frac{d+u}{v}=\frac{d}{f}.$$ De tweede vergelijking is te schrijven als $$\frac{d+u}{d}=\frac{v}{f}.$$ dus $$1+\frac{u}{d}=\frac{v}{f}.$$           We gebruiken de eerste vergelijking om te komen tot $$1+\frac{v}{b}=\frac{v}{f}.$$ Delen door $v$ geeft ten slotte de lenzenformule $$\frac{1}{v}+\frac{1}{b}=\frac{1}{f}.$$