Op de middelbare school wordt heel wat wiskunde gebruikt die eigenlijk te moeilijk is om .cht goed te begrijpen hoe het zit. Op zich is dat helemaal niet erg: we kunnen ook fietsen zonder dat we de ingewikkelde mechanica van de fiets begrijpen.

In het boek Wiskunde in je vingers doen Joost Hulshof en Ronald Meester, twee hoogleraren van de Vrije Universiteit in Amsterdam, een heldhaftige poging om deze wiskunde wél begrijpelijk te maken. Ook zoeken ze vaak naar een meer eenvoudige invalshoek zonder de wiskunde geweld aan te doen.

Het boek heeft drie onderwerpen: normale getallen, het benaderen van functiewaarden zoals bij voorbeeld √2, en waarom in de kansrekening het getal e = 2,718... zo’n belangrijke rol speelt. In de volgende paragraaf geven we een voorbeeld van hun werkwijze.

Raaklijnen en benaderingen

Een vergelijking van de rechte lijn door de oorsprong met helling a wordt gegeven door de formule y = ax. Als we deze lijn p naar rechts en q omhoog verschuiven, krijgen we de vergelijking

$$y – q = a(x – p),$$

ofwel

$$y = q + a(x – p).$$

Wanneer is deze lijn raaklijn aan de grafiek van een functie f door het punt (p, q)? Hulshof en Meester nemen het prettig informele standpunt in dat deze lijn de grafiek van f raakt indien de helling a zo is, dat de lijn het beste past. Als we de grafiek van de functie samen met de raaklijn onder de loep nemen, zien we zo weinig mogelijk verschil. Dit uitgangspunt neemt een hoop moeilijkheden weg en is eigenlijk een beschrijving van de lineaire benadering van de functie bij x = p.

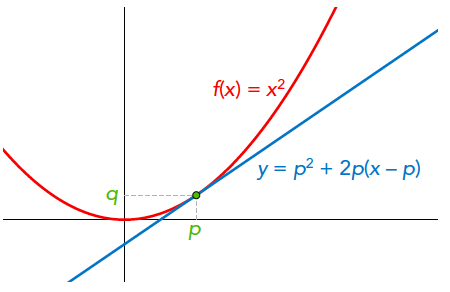
We laten hier zien hoe je de vergelijking van een raaklijn aan de parabool $y = x^2$ in $x = p$ bepaalt (zie ook de figuur rechts). Uitgaand van het merkwaardig product

$$x^2 – p^2 = (x + p)(x – p)$$

is

$$x^2 = p^2 + (x + p)(x – p).$$

In de buurt van p geldt $x + p ≈ 2p$ en door dit in te voeren staat er $x^2 ≈ p^2 + 2p(x – p),$ een benadering die beter wordt naar mate je x dichter bij a neemt. De rechte

$$y = p^2 + 2p(x – p)$$

is de raaklijn aan de parabool voor x = p. Merk op dat we de ‘afgeleide’ 2p nu hebben gevonden z.nder te differentiëren! Dit procedé wordt toegepast op allerlei functies met verrassende resultaten.

Andere onderwerpen

Bovenstaand voorbeeld is exemplarisch voor het boek. Uitgaande van eenvoudige wiskunde worden grote onderwerpen bereikt. Tot de hoogtepunten horen een begrijpelijke benadering van de faculteit en een uitstekende introductie van de normale verdeling.

Wiskunde in je vingers is zeker geen makkelijk boek en sommige opgaven zijn typisch universitaire, in middelbare-schooltaal gestelde opgaven. Dat geeft niks: ze staan meestal aan het eind van een hoofdstuk en lijken soms ingegeven door het geweten van de auteurs. (‘We hebben nog helemaal niet aangetoond waarom de methode convergeert. Convergeert? Moet je dat aantonen?’)

Gratis versie online

Volgens de auteurs is Wiskunde in je vingers bedoeld voor docenten wiskunde in het havo of vwo, voor hun leerlingen in de bovenbouw, maar ook voor liefhebbers die al jaren zoeken naar een toegankelijk, onderhoudend en inspirerend verhaal over wiskunde. Ik geloof dat dat klopt. En wat de normale verdeling betreft, het is een van de weinige echt toegankelijke bronnen.

Het boek is uit 2015, maar recent is ook een gratis online-versie verschenen: http://www.vuuniversitypress.com/wiskunde-in-je-vingers. Toch liever een gedrukte versie? De volledige opbrengst gaat naar twee goede doelen: het Orkest van de Achttiende Eeuw en de Stichting Communication Middle East.