Goed kunnen schudden bij het kaartspelen is natuurlijk al fijn om ervoor te zorgen dat er geen ruzie komt over een oneerlijk voordeel. Soms is het zelfs van levensbelang omdat mensen in het casino gigantische bedragen inzetten, en dan wil je wel zeker weten dat je tegenstander geen voordeel heeft boven jou. En als je toch graag vals wilt spelen, dan is het wel zo prettig om te weten met welke schudtechnieken dat handig kan. Iemand die zeer getalenteerd is in het schudden van kaarten (en ook in zijn eigen voordeel), is Persi Diaconis. Voordat we naar wat statistieken en wiskunde over schudden gaan kijken, zullen we eerst eens terugblikken op de carrière van Diaconis, aangezien deze vrij uitzonderlijk is en ook van groot belang bij de wiskunde van het schudden.

Persi Diaconis is een wiskundige aan de universiteit van Stanford en staat bekend om zijn werk over randomisering, oftewel methodes om iets willekeurig te maken. In het bijzonder valt daar ook het schudden van kaarten onder: we willen met schudden immers zorgen dat een dek zo willekeurig mogelijk is zodat geen speler een voordeel heeft.

Hij is opgegroeid in een muzikaal gezin en heeft zelf tot zijn veertiende viool gespeeld. Vanaf zijn vijfde begon hij zichzelf ook goocheltrucs te leren en dit werd uiteindelijk zijn grootste bezigheid. Hij was zelfs zo verzot op goochelen dat hij op zijn viertiende de middelbare school verliet zonder het aan zijn ouders te vertellen en vervolgens op tour is gegaan met een bekende goochelaar Dai Vernon, ook wel bekend als 'the man who fooled Houdini'. Dai Vernon was een expert in vingervlugheid met kaarten, wat inhoudt dat je kaarten op een kunstige manier kan schudden, maar ook dat je een stapel kan schudden in jouw voordeel. Je kunt bedenken dat Diaconis hier veel van heeft opgestoken.

Na tien jaar scheidden hun wegen en speelde Diaconis in zijn eentje nog een tijdje verder in de clubs van Chicago. Uiteindelijk ging hij terug naar zijn geboorteplaats New York en ging daar wat meer professioneel te werk met goochelen, door nieuwe trucs te bedenken, door lessen te geven over goochelen en door het verzamelen van oude boeken over goochelen. Op een dag ging Diaconis naar een boekenwinkel en kocht daar een befaamd boek van de wiskundige William Feller: Introduction to probability theory and its applications. Dit boek heeft Diaconis de wiskundewereld in getrokken en na een aantal jaar was hij professor aan de Stanford universiteit. Als wiskundige heeft hij onder andere bewezen dat door ongeveer $7$ keer te schudden met de riffle shuffle, zoals afgebeeld in figuur 1, je een stapel van $52$ kaarten willekeurig kan maken.

Statistiek van shufflen

Laten we nu eens naar wat statistieken over schudden kijken. Je kan je afvragen waarom dat nuttig is, maar we zullen bijvoorbeeld zien dat er enorme verschillen zijn in efficiëntie van veelgebruikte schudmethoden. Met kennis over die statistieken kan je dus zorgen dat je een stapel zo snel mogelijk goed kan schudden, maar het levert ook een voordeel op ten opzichte van je tegenstanders als er niet efficiënt wordt geschud: je zou kunnen proberen om de posities van de kaarten in de stapel vast te stellen.

Voor we naar wat statistieken over schudmethoden kijken, moeten we eerst weten wat we verstaan onder een willekeurige stapel kaarten. Een willekeurige stapel kaarten is een stapel kaarten waarbij elke volgorde van kaarten met gelijke kans voorkomt. Dat klinkt misschien een beetje raar, maar stel dat je bezig ben met een potje kaarten en je houdt alle kaarten bij die worden afgelegd tot de pakstapel op is. Om een nieuwe pakstapel te maken gebruik je de kaarten uit de aflegstapel. Als de kaarten uit de aflegstapel niet worden geschud, dan weet jij door het bijhouden precies de volgorde van de kaarten, dus dan is de kans op die volgorde gelijk aan $1$ en de kans op andere volgorden gelijk aan $0$. Door te schudden kan er echter voor worden gezorgd dat je de volgorde helemaal kwijt bent en dan komt elke volgorde voor jou met gelijke kans voor.

Dan nu de vraag: hoe krijg je een willekeurige stapel? Er zijn diverse manieren. De meest eenvoudige manier, ook de manier die wordt gebruikt in pokertoernooien, is die waarbij je de kaarten op de tafel verspreidt en ze vervolgens door elkaar wrijft. Niet erg geavanceerd dus, maar na ongeveer 1 minuut heb je wel een stapel die met heel grote kans volledig willekeurig is. Deze methode staat bekend als smooshing. Een tweede manier van schudden staat bekend als de overhand shuffle. Dit is de veelgebruikte methode waarbij je vanaf de bovenkant van de stapel steeds een klein groepje kaarten pakt en die stapelt in je andere hand, zie figuur 2. Deze is echter niet aan te raden want bij een stapel van $52$ kaarten kan het $10\,000$ keer schudden kosten om een willekeurige stapel te krijgen.

Een derde methode is de al genoemde riffle shuffle. Hierbij verdeel je een stapel kaarten in twee en laat je kleine groepjes kaarten van de twee stapels om en om op elkaar vallen. Deze methode vergt bij $52$ kaarten ongeveer $$7 keer schudden om een willekeurige stapel te krijgen. Dit is al veel beter! Wat hier ook interessant is: als je de riffle shuffle perfect uitvoert, dus als de kaarten van de twee stapels precies om en om op elkaar komen, dan krijg ja na $8$ keer schudden de originele stapel terug. Als je tegenstander dat niet weet heb je natuurlijk een geweldig voordeel. Om dit te bewijzen kun je algebra gebruiken, zie ook het kader onderaan hierover.

Als laatste beschouwen we nog de top-torandom shuffle. Hierbij pak je de bovenste kaart van de stapel en stopt die willekeurig terug in de stapel (wellicht zonder te kijken). Je mag de kaart ook weer terug leggen op de bovenkant, het gaat erom dat de kaart met gelijke kans op elk van de $52$ mogelijk posities terug kan worden teruggestopt in de stapel. Toegegeven, dit is een vrij rare manier van schudden, maar omdat we de kaart willekeurig in de stapel stoppen kan je wel bedenken dat de hele stapel uiteindelijk willekeurig wordt. Hierbij moet je ongeveer $205$ keer schudden, dus na de riffle shuffle zou je denken dat het zinloos is om deze nog voor te stellen. Deze schudmethode leent zich echter goed voor expliciete wiskundige analyse. Persi Diaconis gaf met een aantal collega’s een bewijs voor een stapel met $n$ kaarten. Dit vergt vrij ingewikkelde technieken uit onder andere de coupling theorie, maar in de volgende paragraaf kijken we naar een wat minder net, maar wel makkelijker argument.

Top-to-random Shuffle

Laten we nu eens kijken hoe je ongeveer kan bewijzen dat je bij een stapel van $52$ kaarten zo'n $205$ keer moet schudden met de top-to-random methode om een stapel willekeurig te maken. Algemener zullen we dit zelfs doen voor een stapel van $n$ kaarten. Het idee is om te kijken naar de tijd waarop de onderste kaart in de stapel bovenaan komt te liggen door steeds kaarten willekeurig terug in de stapel te stoppen. Dat is interessant, want de originele onderste kaart kan alleen bovenaan komen door er willekeurig kaarten onder te plaatsen. Omdat kaarten onder de originele onderste kaart willekeurig worden geplaatst, heeft elke volgorde van de kaarten onder de originele onderste kaart een gelijke kans. Dit kunnen we als volgt begrijpen, waarbij we alleen kijken naar het moment waarop een kaart onder de originele onderste kaart wordt geplaatst.

1. Bij de eerste kaart onder de originele onderste is er maar één volgorde mogelijk en die heeft kans $1$.
2. Als er een tweede kaart bij komt, dan kan die boven of onder de eerste kaart komen met gelijke kans, dus beide volgordes hebben gelijke kans.
3. Een derde kaart kan met gelijke kans op een van de drie beschikbare posities komen, en dan heb je $3! = 1 \cdot 2 \cdot 3 = 6$ mogelijke volgordes met gelijke kans.

Zo kunnen we inductief doorgaan tot de originele onderste kaart helemaal bovenaan ligt en je daaronder $(n - 1)!$ volgordes van kaarten hebt met gelijke kans. Als we dan ook de originele onderste kaart willekeurig terug in te stapel stoppen op een van de $n$ posities, heb je een volledig willekeurige stapel. Alle $n \cdot (n - 1)! = n!$ volgordes hebben dan immers een gelijke kans.

We noteren met $T_1$ de tijd waarop er voor het eerst een kaart onder de originele bodemkaart wordt gelegd. We kunnen hebben $T_1 = 1$, als je de eerste keer al een kaart van de bovenkant pakt en deze helemaal onderaan de stapel legt. Maar we kunnen net zo goed hebben $T_1 = 1\,000\,000$, we plaatsen kaarten immers steeds op willekeurig plekken in de stapel. Door het willekeurig plaatsen geldt dat $T_1$ een kansvariabele is. Bij een kansvariabele zijn twee dingen belangrijk: de waarden die de variabele aan kan nemen en de kansen op die waarden. Allereerst de waarden: de kleinst mogelijk waarde is $1$ omdat je wel eerst een kaart in de stapel moet stoppen om überhaupt een kans te hebben dat die kaart onder de originele onderste kaart komt. Van een bovengrens is echter geen sprake, het kan immers voorkomen dat kaarten steeds niet onder de onderste kaart worden gelegd. De verzameling van waarden die T1 dus aan kan nemen is $\{1, 2, 3, 4, \dots\}$.

Dan nu de kansen: gegeven een getal $k$ in ${1, 2, 3, 4, \dots}$, wat is de kans op $T_1 = k$? Die kans zullen we noteren met $P(T_1 = k)$. Aangezien je bij het terugleggen van een kaart $n$ posities hebt om te kaart terug te leggen en aangezien elke positie een gelijke kans heeft, is er bij elke teruglegging precies een kans van $\tfrac{1}{n}$ dat de kaart wordt teruggelegd onder de onderste kaart. Dat betekent ook dat er een kans is van $1-\tfrac{1}{n} = \frac{n-1}{n}$ dat de kaart niet wordt teruggelegd onder de onderste kaart. Maar hoe berekenen we dan $P(T_1 = k)$? Dan moeten we bedenken wat $T_1 = k$ betekent. Blijkbaar is er bij de eerste $k - 1$ keer schudden nog geen kaart onder de onderste kaart gelegd. Dan heb je dus de maken met de gebeurtenis

de eerste kaart komt niet onder de onderste en de tweede kaart niet en de derde kaart niet, ... en de $k - 1$-ste kaart niet.

Als je een gebeurtenis hebt met 'en', dus waarbij dingen tegelijk gebeuren, dan moet je de kans op de verschillende dingen met elkaar vermenigvuldigen. Eigenlijk moeten de 'dingen' tussen de 'en' ook onafhankelijk van elkaar zijn, maar dat is hier ook het geval, een eerste kaart die niet onder de onderste komt is onafhankelijk van een tweede kaart met die eigenschap, etc. Aangezien elk van de 'dingen' hier kans $\frac{n-1}{n}$ heeft, heb je dus een kans van

$$\left(\frac{n-1}{n}\right)^{k-1}$$

dat je bij de eerste $k - 1$ keer schudden nog geen kaart onder de onderste hebt gelegd. Maar we hebben $T_1 = k$, dus bij de $k$-de keer schudden komt er wel eindelijk een kaart onder de onderste! Die gebeurtenis heeft een kans van $\tfrac{1}{n}$ en omdat we dan nog een onafhankelijke 'en' hebben, wordt zo de totale kans op $T_1 = k$ dus

$$P(T_1=k)=\frac{1}{n}\cdot\left(\frac{n-1}{n}\right)^{k-1}.$$

Hiermee hebben we dus ook de kansverdeling van $T_1$ bepaald. Deze kansverdeling staat bekend als een geometrische kansverdeling met succeskans $\tfrac{1}{n}$. 

Nadat er één kaart is gelegd onder de originele onderste kaart, zijn we even blij, maar uiteindelijk willen we dat alle kaarten onder de onderste kaart komen te liggen. Laten we nu dus kijken naar de tijd $T_2$, geteld na tijd $T_1$, waarop er voor het eerst een tweede kaart onder de originele bodemkaart wordt geplaatst. Voor $T_2$ hebben we ook als verzameling van mogelijke waarden de verzameling $\{1, 2, 3, 4, \dots\}$, het kan immers willekeurig lang duren voor er een tweede kaart onder de originele onderste kaart wordt gelegd. Aangezien er al één kaart onder de originele onderste kaart ligt, zijn er nu twee posities onder de originele onderste kaart om een kaart willekeurig terug te leggen. Er is dus een kans van $\tfrac{2}{n}$ dat een kaart onder de originele onderste kaart wordt geplaatst, en dus ook een kans van $1-\tfrac{2}{n}=\frac{n-2}{n}$ dat een kaart niet onder de originele onderste kaart wordt gelegd. Nu willen we de kansverdeling van $T_2$ bepalen en dat kunnen we op dezelfde manier doen als we hebben gedaan voor $T_1$. De gebeurtenis $T_2 = k$ betekent nu:

bij de eerste $k- 1$ keer schudden na tijd $T_1$ wordt er nog geen tweede kaart gelegd onder de originele onderste kaart, maar bij de $k$-de keer wel.

Probeer nu eens met de bovenstaande omschrijving zelf te achterhalen waarom we krijgen

$$P(T_2=k)=\frac{2}{n}\cdot\left(\frac{n-2}{n}\right)^{k-1}.$$

Het bovenstaande kunnen we nu herhalen tot de originele onderste kaart helemaalbovenaan de stapel komt te liggen. We beschouwen dus steeds de variabele

$T_i$ = aantal keer schudden na tijd $T_{i-1}$ tot er voor het eerst een $i$-de kaart onder de originele onderste kaart ligt.

voor $1 \le i \le n - 1$ en met $T_0 = 0$. Voor alle i vinden we dan

$$P(T_i=k)=\frac{1}{n}\cdot\left(\frac{n-1}{n}\right)^{k-1}$$

voor $k$ in ${1, 2, 3, 4, \dots}$. Oftewel, de variabele $T_i$ heeft een geometrische kansverdeling met succeskans $\tfrac{i}{n}$.

Nu zijn we bijna klaar. We willen de tijd weten waarop de originele onderste kaart bovenaan de stapel ligt door het schudden. Per definitie weten we dat er na tijd $T_1$ precies één kaart onder de originele onderste kaart ligt en na tijd $T_1 + T_2$ ligt er voor het eerst een tweede kaart onder de originele onderste kaart, we tellen $T_2$ immers na $T_1$. Als we zo doorgaan kunnen we vinden dat er na tijd $T_1 + \dots + T_{n-1}$ precies $n - 1$ kaarten onder de originele onderste kaart liggen, dus dan moet die kaart wel bovenaan liggen. Als we dan nog een keer schudden, dan pakken we de originele onderste kaart en leggen die willekeurig terug in de stapel. Op dat moment is de stapel volledig willekeurig, oftewel, in tijd

$$T=T_1+\dots+T_{n+1}+1$$

is de stapel volledig willekeurig. De '$+1$' is voor de laatste keer schudden met de oorspronkelijk onderste kaart.

We weten dus dat de stapel goed is geschud na tijd $T$, maar dit is een willekeurige tijd, dus daar hebben we nog niet heel veel aan. Een manier om iets meer informatie te krijgen is om bijvoorbeeld het gemiddelde van tijd $T$ te berekenen, of iets netter, de verwachting(swaarde) van $T$. De verwachting van een kansvariabele $X$ noteren we als $\mathbb{E}[X]$. Een belangrijke en elementaire regel over verwachtingen is de volgende: voor twee kansvariabelen $X$ en $Y$ geldt dat

$$\mathbb{E}[X + Y] = \mathbb{E}[X] + \mathbb{E}[Y].$$

Oftewel, de verwachting van de som van $X$ en $Y$ is hetzelfde als de som van de verwachtingen. En in plaats van twee geldt dit net zo goed voor sommen van willekeurig veel kansvariabelen. We kunnen dus vinden dat

$$\mathbb{E}[T] = \mathbb{E}[T_1+\dots+T_{n-1}+1] = \mathbb{E}[T_1] + \dots + \mathbb{E}[T_{n-1}]+1,$$

waarbij we hebben gebruikt dat $\mathbb{E}[1]=1$. De verwachting van een constante (dat is dus geen kansvariabele meer) is immers zichzelf. Nu moeten we dus alleen nog $\mathbb{E}[T_1]$ en $\mathbb{E}[T_2]$ tot en met $\mathbb{E}[T_{n-1}]$ berekenen. Zoals we eerder hebben gezien hebben alle variabelen $T_i$ een geometrische kansverdeling met succeskans . Voor een geometrische variabele $X$ met succeskans $p$ kun je vinden dat

$$\mathbb{E}[X] = \tfrac{1}{p}.$$

Dat geeft in ons geval dus $\mathbb{E}[T_1] = n/1$, $\mathbb{E}[T_2] = n/2$, $\mathbb{E}[T_3] = n/3$ tot en met $\mathbb{E}[T_{n-1}] = \frac{n}{n-1}$. Oftewel,

$$\mathbb{E}[T] = \tfrac{n}{1}+\tfrac{n}{2}+\tfrac{n}{3}+\dots+\tfrac{n}{n-1}+\tfrac{n}{n} = n\cdot\left(\tfrac{1}{1}+\tfrac{1}{2}+\tfrac{1}{3}+\dots+\tfrac{1}{n}\right),$$

waarbij we hebben gebruikt dat $1=\tfrac{n}{n}$. Om deze berekening af te maken hebben we nog een laatste ingrediënt nodig. namelijk, naarmate $n$ groot wordt, zal gelden dat 

$$\tfrac{1}{1}+\tfrac{1}{2}+\tfrac{1}{3}+\dots+\tfrac{1}{n}\approx \ln(n).$$

Nu denk je misschien: 'wat is $\ln(n)$ nou weer?' Wel, dit is de natuurlijke logaritme van $n$. Deze functie kom je vast tegen in de bovenbouw, maar anders moet je maar eens op je rekenmachine kijken, er is een knopje voor! Op deze manier hebben we een vrij eenvoudige benadering van $\mathbb{E}[T]$, namelijk $n \cdot \ln(n)$.

Nu rest natuurlijk de vraag, waar komt dan die $205$ vandaan voor het gemiddelde aantal keer schudden via de top-to-random methode om een willekeurige stapel van $52$ kaarten te krijgen? Nou, met wat we net hebben afgeleid kunnen we dat vrij eenvoudig vinden. Namelijk, neem $n = 52$ en vul het in voor de benadering van $\mathbb{E}[T]$, dat geeft

$$\mathbb{E}[T] \approx \cdot \ln(52) = 205{,}464\dots \approx 205.$$

Dezelfde wiskunde voor verschillende problemen

Wellicht komt de bovenstaande wiskundige analyse je bekend voor. In Pythagoras 61-3 hebben we het artikel Spaar ze allemaal! gezien. Hierin werd de vraag gesteld hoeveel voetbalplaatjes je gemiddeld moet sparen om je collectie compleet te krijgen. Daarbij werd bijna dezelfde analyse gegeven als hierboven voor het bepalen van het gemiddelde aantal keer schudden om een willekeurige stapel kaarten te krijgen met de top-to-random shuffle. Dit is een mooi voorbeeld van de kracht van wiskunde: een algemene wiskundige analyse, in dit geval met de geometrische kansverdeling, stelt ons in staat om talloze ogenschijnlijk verschillende problemen op te lossen.

 

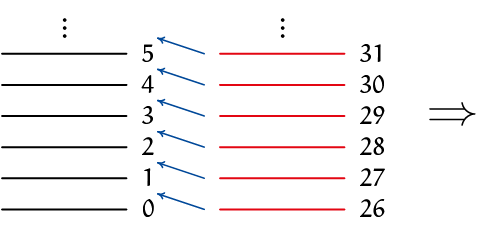
		8 perfeCte riffle shuffles na elkaar is een nuloperatie door Paul Levrie Het is eenvoudig te bewijzen dat 8 keer na elkaar op dezelfde manier een perfecte riffle shuffle uitvoeren met 52 speelkaarten de originele volgorde van de kaarten herstelt. Bij een perfecte shuffle verdeel je de speelkaarten in 2 stapels van 26 kaarten, en schuif je ze zo in elkaar dat de kaarten van beide stapels om en om komen te zitten. Links de twee stapels, kaarten genummerd van $0-25$ en van $26-51$. Rechts zie je het resultaat van het in elkaar schuiven, waarbij je er steeds voor zorgt dat kaart $0$ onderaan blijft. Rechts van de kaarten staat het oude rangnummer van de kaarten, links het nummer van hun nieuwe plaats in de stapel. Merk op dat het nieuwe nummer in de stapel als volgt uit het oude rangnummer volgt: nieuwe positie = oude positie maal $2$. En als je dan boven de $51$ uitkomt: er $51$ van aftrekken. Bijvoorbeeld: $2$ wordt $4$; $28$ wordt $28 \times 2 = 56$, $56 - 51 = 5$. Hetzelfde gebeurt bij een tweede perfecte shuffle, we geven een voorbeeld: we starten met de kaart met rangnummer $47$. shuffle $1 \rightarrow 47 \times 2 = 94 \rightarrow 94 - 51 = 43$ shuffle $2 \rightarrow 43 \times 2 = 86 \rightarrow 86 - 51 = 35$ Dus deze kaart eindigt na $2$ shuffles op positie $35$. Merk op dat je ook anders kan tellen: bij twee perfecte shuffles vermenigvuldig je het rangnummer tweemaal met $2$ en dan trek je van het resultaat dát veelvoud van $51$ af waarmee je eindigt tussen $0$ en $51$: $$47 \rightarrow 47 \times 2 = 94 \rightarrow 94 \times 2 = 188 - 3 \times 51 \rightarrow 35.$$ We voeren nu $8$ perfecte shuffles na elkaar uit. Waar komt de kaart op beginpositie $n$ terecht? De nieuwe positie van die kaart is dan … deze beginpositie: $$n \rightarrow 2n \rightarrow 4n \rightarrow 8n \rightarrow \dots \rightarrow 2^8n = 256n;$$ $$256n = (1+5\cdot 51)n = n+5n\times 51 - 5n \times 51 = n.$$