Inleiding

Een forensisch laboratorium bekijkt op een aantal plekken (loci genoemd, enkelvoud locus) op de chromosomen welke DNA-varianten mensen daar hebben zitten. Omdat iedereen elk chromosoom in tweevoud heeft, eentje gekregen van de moeder en eentje van de vader (afgezien van de geslachtschromosomen, die laten we hier buiten beschouwing), levert dit op elke onderzochte locus een zogenaamd genotype $g$ op dat we aangeven met het (ongeordende) getallenpaar $g = (a_1, a_2)$. We noemen $a_1$ en $a_2$ de allelen van deze locus. Je kunt niet zien welk allel van de moeder en welk van de vader afkomstig is.

In dit artikel beperken we ons tot één locus. Als we begrijpen hoe we hiermee iets over verwantschap kunnen zeggen is de uitbreiding naar meer loci niet zo heel moeilijk meer, omdat de verschillende loci zich tamelijk onafhankelijk van elkaar gedragen.

Een mens heeft 23 paar chromosomen: één afkomstig van de vader en één van de moeder. Aan een chromosoom zitten twee eindstukken of telomeren. Op deze telomeren zijn allerlei plaatsen (loci, zie figuur 2) aan te wijzen waar zich een gen bevindt. Dit gen komt voor in allerlei varianten, maar zit links en rechts op precies de zelfde plek. Voor de helft is het gen dus bepaald door een erfelijke streng van de vader en voor de andere helft uit een streng van de moeder. Deze twee (dubbele) DNA-strengen heten allelen. We associëren met deze allelen een getallenpaar $(a_1, a_2)$ waarbij niet te bepalen is welke van de twee getallen bij de vader en welke bij de moeder behoort. (Zie figuur 1)

 

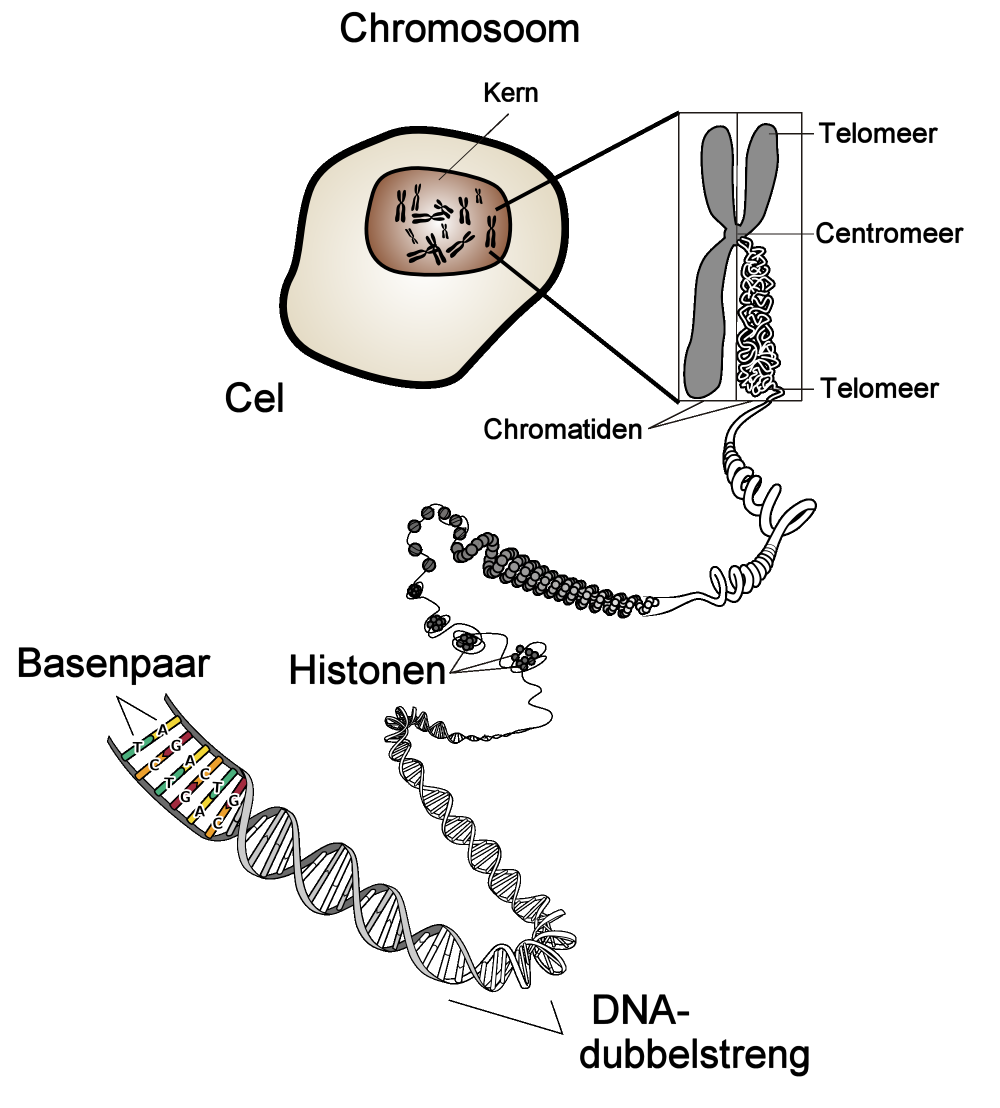
Verwantschap

Wanneer iemand een kind krijgt, zal $a_1$ of $a_2$ doorgegeven worden aan het kind. Bij elk kind is dit een nieuwe willekeurige keuze, waarbij de allelen met gelijke kans worden gekozen. Elke ouder en kind hebben dus minstens één allel gemeenschappelijk op elke locus.

Een belangrijk concept in verwantschapsonderzoek is dat allelen van personen in de stamboom identiek door overerving (IDO) kunnen zijn. Dit betekent dat ze beiden hetzelfde allel van een gemeenschappelijke voorouder (ouder, grootouder, ...) hebben geërfd.

Als we inteelt uitsluiten dan kunnen de twee ouders van een persoon geen familie van elkaar zijn. Dat betekent dat het niet mogelijk is dat de twee allelen van die persoon, die van vader en moeder gekregen zijn, met elkaar IDO zijn.

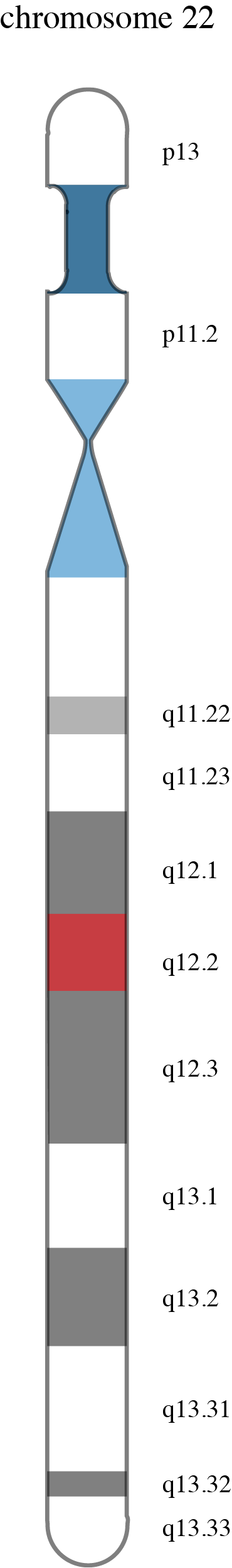
Laten we nu eens kijken naar de genotypes $(a_1, a_2)$ respectievelijk $(b_1, b_2)$ van twee personen $R$ en $S$.

1. Geen van de $a_i$ is IDO met een $b_j$; in dat geval kunnen we $R$ en $S$ wat betreft de relatie tussen hun genotypes als niet verwant beschouwen.
2. Er is precies één $a_i$ die IDO is met een $b_j$; in dat geval is de statistische relatie tussen de genotypes van $R$ en $S$ dezelfde als die tussen een ouder en kind die immers ook precies één IDO allel hebben.
3. Zowel $a_1$ als $a_2$ zijn IDO met een van de $b_j$; in dat geval hebben $R$ en $S$ dus hetzelfde genotypes, en kunnen we ze wat verwantschap betreft beschouwen als eeneiïge tweelingen.

Uit deze inventarisatie blijkt dat er wat betreft IDO allelen drie ‘basis-verwantschappen’ zijn: (1) geen verwantschap, (2) ouder-kind, en (3) eeneiïge tweelingen.

Laat nu voor twee verwante personen $R$ en $S$ de kans dat deze twee personen $i$ allelen IDO hebben genoteerd worden door $\kappa_i(R,S)$.

Dit levert de vector $\kappa(R,S) = (\kappa_0(R,S), \kappa_1(R,S), \kappa_2(R,S))$ op. Laten we als voorbeeld naar twee broers kijken. Het kan zijn dat de vader aan de twee broers verschillende allelen doorgeeft, en de moeder ook. Dat gebeurt met kans $1/2 \times 1/2 = 1/4$. In dat geval hebben de broers geen enkel allel IDO, dus $\kappa_0(R,S) = 1/4$. Als zowel de vader als de moeder hetzelfde allel aan de twee broers doorgeven hebben ze twee allelen IDO, en dit gebeurt met kans $1/2 \times 1/2 = 1/4$, dus $\kappa_2(R,S) = 1/4$. Tenslotte kan de vader wel maar de moeder niet hetzelfde allel doorgeven, of andersom, en dat levert op dat $\kappa_1(R,S) = 1/2$. In het geval van twee broers is dus

$$\kappa(R,S) = \left(\frac{1}{4},\frac{1}{2},\frac{1}{4}\right).$$

De vector $\kappa(R,S)$ is voor elk tweetal personen $R$ en $S$ binnen een familiestamboom te bepalen, maar dat is vaak nog niet eens zo eenvoudig. Wat makkelijker te berekenen is, en soms een goede eerste stap naar $\kappa(R,S)$, is de kans dat als je uit elk van de genotypes van twee gegeven personen $R$ en $S$ een willekeurig allel kiest, deze twee gekozen allelen IDO zijn. Als we die kans $\theta_{R,S}$ noemen dan geldt dat 

$$\theta_{R,S} = \frac{1}{4}\kappa_1(R,S) + \frac{1}{2}\kappa_2(R,S)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$$ 

Immers, als $R$ en $S$ één allel IDO hebben, dan is de kans 1/4 dat ze allebei gekozen worden, en als ze er twee IDO hebben, is de kans 1/2 dat de twee keuzes precies een IDO paar vormen. Bijvoorbeeld voor broers $R$ en $S$ geldt dan dus dat

$$\theta_{R,S} = \frac{1}{4}\cdot \frac{1}{2} +  \frac{1}{2}\cdot \frac{1}{4} =  \frac{1}{4} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$$

Stel nu dat $R$ en $S$ een gemeenschappelijke voorouder $A$ hebben, en dat er $n_1$ generatiestappen zijn van $A$ naar $R$ en $n_2$ van $A$ naar $S$. De gemeenschappelijke voorouder $A$ zal nu een van zijn of haar twee allelen richting $R$ doorgeven, en een nieuwe random trekking doen voor het allel dat richting $S$ ‘vertrekt’ in de stamboom. Met kans 1/2 is dat twee keer hetzelfde allel, en vertrekken er vanuit $A$ dus twee IDO allelen richting $R$ en $S$. De kans dat die twee allelen dan ook daadwerkelijk bij $R$ en $S$ aankomen is $(1/2)^{n_1}(1/2)^{n_2}$, want bij elke volgende generatie is de kans 1/2 dat het allel verder wordt doorgegeven. De kans dat $R$ en $S$ van $A$ twee IDO allelen krijgen is dus $(1/2)^{n_1+n_2+1} = (1/2^{n_A}$ met $n_A = n_1 + n_2 +1$. Natuurlijk kunnen $R$ en $S$ meer dan één gezamenlijke voorouder hebben (bijvoorbeeld dezelfde opa en oma), maar voor elk van deze voorouders geldt dan de zojuist gevolgde redenering. Hierbij zijn alleen die gemeenschappelijke voorouders van belang die het ‘dichtstbij’ zijn in de familiestamboom, het meest recent dus. Een vader van een gemeenschappelijke voorouder $A$ hoeft niet verder bekeken te worden omdat eventuele IDO allelen van die vader via $A$ moet gaan. Het gaat dus alleen om die voorouders waarbij precies de twee familielijnen vanuit $R$ en $S$ samenkomen. Met andere woorden, we krijgen

$$\theta_{R,S} = \sum_A \left(\frac{1}{2}\right)^{n_A}$$

waarbij de som over de beschreven gemeenschappelijke voorouders van $R$ en $S$ loopt. Laten we nu ter illustratie twee specifieke familierelaties bekijken.

Neven. Twee neven hebben één stel grootouders gemeenschappelijk. Voor elk van deze grootouders geldt dat $n_1 = n_2 = 2$ en dus is $\theta_{R,S} = 2\times (1/2)^5 = 1/16$. Omdat voor neven geldt dat $\kappa_2(R,S) = 0$ (ga dit na!), vinden we nu met behulp van (1) dat $\kappa_1(R,S) = 1/4$ en dus dat $\kappa_0(R,S) = 3/4$.

Dubbele neven. Dit zijn personen $R$ en $S$ zodanig dat elke ouder van $R$ een broer of zus is van een ouder van $S$. Er zijn nu vier grootouders in het spel, en voor dubbele neven is dus $\theta_{R,S} = 4\times (1/2)^5 = 1/8$. Echter, nu kunnen we wel degelijk twee IDO allelen hebben tussen de dubbele neven. Dit gebeurt als de ouders van $R$ en de ouders van $S$ allebei dezelfde IDO allelen doorgeven. Stel bijvoorbeeld dat de vaders van $R$ en $S$ broers zijn. Zij geven elk een willekeurig allel door aan $R$ en aan $S$, en we hebben in (2) gezien dat de kans dat twee willekeurige allelen van broers IDO zijn, gelijk is aan 1/4. Hetzelfde moet gebeuren bij de moeders van $R$ en $S$ (die zussen zijn), en dus is $\kappa_2(R,S) = 1/16$ voor dubbele neven. Maar omdat $\theta_{R,S} = 1/8$, moet $\kappa_1(R,S) = 3/8$ wegens (1), en dus $\kappa_0(R,S) = 9/16$.

Vaderschapstesten

Gegeven is een kind $T$ met genotype $g_T$ en een mogelijke vader $R$. Forensisch laboratoria berekenen eerst de kans op het genotype $g_T$ van het kind gegeven dat $R$ inderdaad de vader is. Daarna bepalen ze de kans dat het kind dit genotype zou hebben met een willekeurige gekozen man als vader. Door deze kansen met elkaar te vergelijken meet je hoeveel gemakkelijker het is het genotype van het kind te verklaren met, dan wel zonder vaderschap van de mogelijke vader $R$. 

Het quotiënt van die kansen noteren we met PI$(R, T)$ (PI staat voor parental index). Als PI>1, dan is het genotype van het kind makkelijker te verklaren onder de aanname dat $R$ de vader is dan onder de aanname dat een willekeurige man de vader is, en zodoende biedt dit dan steun voor de hypothese dat $R$ de vader is. Als PI< 1 is het precies andersom, en als PI = 1 is het bewijs neutraal. 

Wat nu als R beweert dat niet hij, maar zijn verwant $S$ de vader is van $T$? Om daar iets over te zeggen kunnen we de coëfficiënten van daarnet gebruiken. Immers, als de claim van $R$ klopt, dan hebben we sowieso dat $\kappa_2(R, T) = 0$. Verder hebben we dan dat

$$\kappa_1(R, T) =\frac{1}{2}\kappa_1(R,S) + \kappa_2(R,S) = 2\theta_{R,S}.\ \ \ \ \ (3)$$

Immers, $R$ en $T$ kunnen alleen maar een IDO allel hebben als $S$ een IDO allel met $R$ doorgeeft aan $T$, en de laatste gelijkheid volgt uit (1). Omdat $\kappa_0(R, T) + \kappa_1(R, T) + \kappa_2(R, T) = 1$ volgt nu dat

$$\kappa_0(R, T) = \kappa_0(R,S) + \frac{1}{2}\kappa_1(R,S) = 1− 2\theta_{R,S}.\ \ \ \ \ \ \ \ (4)$$

Wat zegt dit nu over de verhouding tussen de kansen op het genotype van het kind $T$ als de claim van $R$ klopt, ten opzichte van de kans op het genotype van het kind als een willekeurige onbekende man de vader is? Welnu, de claim dat $S$ de vader is van $T$ is equivalent met de claim op een specifieke relatie tussen $R$ en $T$ die volgt uit de familierelatie tussen $S$ en $R$ en het vaderschap van $S$ van $T$. Als $R$ en $S$ bijvoorbeeld broers zijn, dan is de claim op vaderschap van $S$ genetisch equivalent met de claim dat $R$ de oom is van $T$. 

De kans dat $R$ en $T$ genotypes respectievelijk $g_R$ en $g_T$ hebben wordt gegeven door

$$\sum^2_{i=0} \kappa_i(R, T)P_i(g_R, g_T )$$

waarbij $P_i(g_R, g_T)$ staat voor de kans op genotypes $g_R$ voor $R$ en $g_T$ voor $T$ als $R$ en $T$ $i$ allelen IDO hebben. Vanwege (3) en (4) is deze uitdrukking gelijk aan $$(1 − 2\theta_{R,S})P_0(g_R, g_T) + 2\theta_{R,S}P_1(g_R, g_T ).$$

Als niet $S$ maar een willekeurige, ongerelateerde man de vader is van $T$, dan zijn $R$ en $T$ ook ongerelateerd, en is de kans op de gegeven genotypes $g_R$ en $g_T$ gelijk aan $P_0(g_R, g_T)$. Dus de verhouding tussen de kansen op $g_R$ en $g_T$ onder enerzijds de gegeven relatie (in de teller), en geen familierelatie anderzijds (in de noemer), wordt gegeven door 

$$\frac{(1 − 2\theta_{R,S})P_0(g_R, g_T) + 2\theta_{R,S}P_1(g_R, g_T)}{P_0(g_R, g_T)} = 1− 2\theta_{R,S} +2\theta_{R,S}\frac{P_1(g_R, g_T)}{P_0(g_R, g_T)}$$

en dit moet dan ook de steun zijn voor het vaderschap van $S$, want dat vaderschap is equivalent met de specifieke familierelatie tussen $R$ en $T$. Het quotiënt in de laatste regel is de kans op de genotypes van $R$ en van $T$ gegeven dat ze één allel IDO hebben gedeeld door de kans dat ze geen allel IDO hebben. Dat is hetzelfde als de kans op de genotypes gegeven dat $R$ de vader is van $T$ gedeeld door de kans op de genotypes gegeven dat een willeurig persoon de vader is. Dit is niets anders dan PI$(R, T)$, dus de formule reduceert tot

$$\text{PI}(S, T) = 1− 2\theta_{R,S} +2\theta_{R,S}\text{PI}(R, T) = 1+2\theta_{R,S}(\text{PI}(R, T) − 1).$$

Op deze manier kan je dus, gegeven een man $R$ en een kind $T$, uit de directe ouder-kind vergelijking niet alleen bepalen hoe goed de verklaring is dat $R$ de vader is van $T$ ten opzichte van een willekeurige persoon. Dankzij de IDO-coëfficiënten kan je ook onmiddellijk de steun bepalen voor ouderschap voor elke andere mogelijk type verwant van $R$. Tevens zie je dat wanneer PI$(R, T)$ > 1, dus als er steun is voor vaderschap van $R$ omdat het profiel van het kind beter verklaard kan worden met $R$ als vader dan zonder $R$ als vader, er ook meteen steun is voor vaderschap van elke verwant van $R$, hoe ver ook!