Kleine nootjes zijn eenvoudige opgaven die weinig of geen wiskundige voorkennis vereisen om opgelost te worden. De antwoorden vind je onderaan zodra het volgende nummer van Pythagoras verschenen is.

 

PALINDROOMOPTELLING

Neem eens de getallen 19 en 92. Zet de twee 9’s onder elkaar en tel ze op (19 wordt dus 190). Het resultaat is een palindroomgetal (leest van achter naar voren hetzelfde).

19
  92
---- +
282

Zoek nu drie getallen: $ab$9, $c$9$d$ en 9$ef$ met $a$ t/m $f$ ongelijk aan elkaar en geen 9. Zet ze onder elkaar met de 9’s onder elkaar en tel ze weer op. Dan staat er weer een palindroomgetal.
Zoek een oplossing voor de cijfers $a$ t/m $f$.

 

TWEE UIT VIJF?

Je hebt vijf gewichtjes die er gelijk uitzien. Je weet dat twee ervan een gelijk gewicht hebben, dat kleiner is dan dat van de drie andere, die ook een gelijk gewicht hebben. Je mag drie keer een balans gebruiken. Bepaal welke twee de lichtste zijn.

 

ALLE ‘ZANDLOPERS’

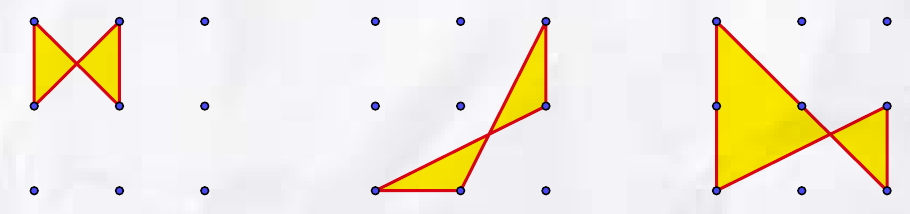
Neem een vierkant rooster van 3 × 3 = 9 punten. Je kunt daarin allerlei ‘zandlopers’ (met gekleurde inhoud) tekenen. In de figuur zijn er een paar gegeven. Hoeveel verschillende kun je er maken? Als twee zandlopers door spiegeling, rotatie of translatie op elkaar kunnen vallen, tellen ze als een enkele.

 

FISCHERSCHAAK

De legendarische Amerikaanse schaker Bobby Fischer heeft ooit voorgesteld om de beginstand van de stukken op de eerste rij willekeurig te maken. Dit om het spel minder afhankelijk te maken van de standaardopeningstheorie. Fischer legde wel twee beperkingen op. De twee lopers moeten op velden van verschillende kleur staan. En verder moet de koning tussen de twee torens komen te staan (eventueel met andere stukken), dit om het rokeren mogelijk te maken.
Het heet ook wel Fischer Random Chess of Fischer960, omdat er 960 mogelijke beginstanden zijn.

• Toon aan dat het aantal 960 is.

• Hoeveel mogelijkheden zijn er, als je alleen de eerste eis laat vallen? (Lopers mogen op gelijke kleur staan.)

• Hoeveel mogelijkheden zijn er, als je alleen de tweede eis laat vallen? (Koning hoeft niet ergens tussen de torens in te komen.)

• Hoeveel mogelijkheden zijn er, als je beide eisen laat vallen?

 

TOREN SLAAT TOREN?

Op een klein schaakbord van 3x3=9 velden staan alleen een rode en een zwarte toren, op de velden A1 en B2. Ze kunnen elkaar niet slaan. (Een toren mag in een zet naar een willekeurig ander veld op zijn verticale kolom of op zijn horizontale rij. Hij mag niet over de andere toren heen springen. Hij mag, indien mogelijk wel de andere toren slaan.)

• Eerst doet de de speler met de rode toren een willekeurige zet (wel volgens de regels). Daarna doet de speler met de zwarte toren een willekeurige zet.
  Hoe groot is de kans dat de tweede speler de eerste toren heeft geslagen?

• Eerst zet rood, dan zwart en dan (eventueel) weer rood.
  Hoe groot is de kans dat rood de zwarte toren slaat?