KIPNUGgeTSGETAL

Bij een fastfoodketen kun je kipnuggets krijgen in porties van $6, 9 {\rm\ of\ } 20$. Als je zin hebt in $18$ stukjes, neem je $3$ porties van $6$. Als je er wel $35$ wilt eten, neem je porties van $6, 9 {\rm\ en\ } 20$. Sommige porties kun je niet precies bestellen, zoals $5$ of $8$.

Wat is het grootste aantal dat je niet exact kunt bestellen? Dat is het kipnuggetsgetal.

(Met dank aan Michel van den Heuvel.)

PIRAMIDE aFBReKEN

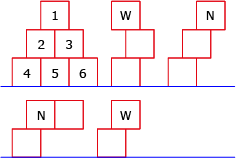
Een piramide bestaat uit 6 kubusvormige blokken. Zie de figuur. Het doel is de piramide blok voor blok af te breken, zodat er dus na het verwijderen van zes blokken niets meer staat. Theoretisch bestaan er dan $6 \times 5 \times 4 \times 3 \times 2 \times 1 = 6! = 720$ mogelijke volgordes. Soms moet er voorzichtig een blok uitgeschoven worden. Maar bij sommige volgordes valt er een blok of kiepert er een stapeltje om. Dat mag niet. Een blok dat voor de helft oversteekt mag net wel. In de figuur staat een aantal stapels die wel (W) ‘onderweg’ mogen en een aantal die niet mogen (N).

Hoeveel verschillende mogelijke volgordes zijn er om de piramide in zijn geheel af te breken?

BoER ZOEKT BLoeMBED

Boer Anema heeft $40$ stukken hek van elk $2$ meter. Hij wil een rechthoekig stuk land omheinen met die hekken om daarin een bloembed te maken. Daaromheen wil hij een tweede omheining maken. Tussen de eerste en tweede omheining wil hij een looppad maken. De oppervlakte van het bloembed wil hij $2$ keer zo groot maken als de oppervlakte van het looppad. Het looppad is overal even breed.

Wat zijn de afmetingen van bloembed en looppad?

WELKE VAN DE nEGEN?

Je hebt negen gewichtjes met erop geschreven: $1, 2, 3, 4, 5, 6, 7, 8 {\rm\ en\ } 9$ gram. Acht van de negen wegen precies wat erop staat. Het negende gewichtje is een heel klein beetje lichter dan erop staat. Je mag twee keer met een balans wegen. Bepaal hoe je dat moet doen om in alle gevallen het afwijkende gewichtje te kunnen aangeven.

BIJZONDErE DATUM

Ria en Jan hebben elkaar op de middelbare school leren kennen op 11 april 1963. Al gauw zei Jan: ‘Dat is een bijzondere datum, want $11 \times 04 + 19 = 63$.’

Dus: dag maal maand plus eeuw is jaar. Die data vieren zij. Soms zijn er wel meer in een jaar.

• Op welke datum gold deze bijzonderheid voor het eerst weer na 11 april 1963?
• In welk jaar vierden zij het meeste van hun bijzondere dagen?