Enen en drieën delen door twee

Een natuurlijk getal $N$ bestaat uit $2n$ cijfers, afwisselend $1$ en $3$. Als je dit getal deelt door $2$ krijg je (nullen aan het eind niet meegeteld):

1. Een getal van $2n$ cijfers, afwisselend $5$ en $6$, waarvan de laatste $6$ achter de komma
2. Een getal van $2n$ cijfers, afwisselend $6$ en $5$, waarvan de laatste $5$ achter de komma
3. Een getal van $n$ cijfers, afwisselend $5$ en $6$, waarvan de laatste $6$ achter de komma
4. Een getal van $n$ cijfers, afwisselend $6$ en $5$, waarvan de laatste $5$ achter de komma
5. Antwoord niet gegeven

Deelbaarheid

Wat is het grootste natuurlijke getal dat deelbaar is door alle getallen kleiner dan zijn vierkantswortel?

 

SChooljongens en -meisjes

In een school van $100$ leerlingen zitten $a$ meisjes en $b$ jongens. $a$ is niet deelbaar door $10$. Wat is de som van de cijfers van $a$ en $b$?

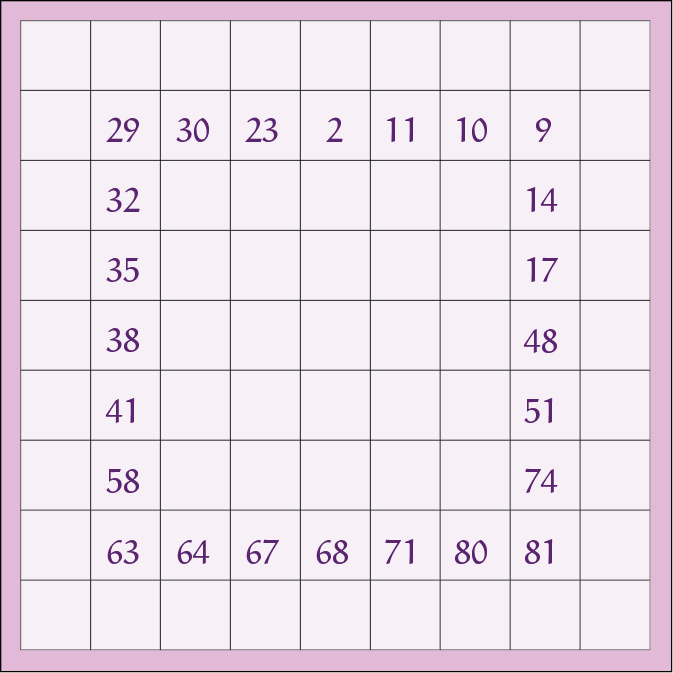
Numbrix

Het vierkant moet gevuld worden met een keten van de getallen $1$ t/m $81$. De getallen die het pad vormen mogen elkaar alleen horizontaal of verticaal raken.

Romeinse stoelendans

Op een Romeins feestje wordt een stoelendans gehouden. $10$ mannen nemen deel met $9$ stoelen.

De muziek begint en de mannen lopen rondjes rond de stoelen. Als de muziek stopt moeten de mannen gaan zitten, degene die geen zitplaats heeft, valt af. Elke spelronde wordt er een stoel weggenomen. Stel dat de kans om geen stoel te vinden elke spelronde volstrekt gelijk verdeeld is over de mannen.

Als Claudius bij de laatste $6$ mannen hoort (met $5$ stoelen) wat is de kans dat hij een plaats bemachtigt bij de laatste $3$ (met $2$ stoelen)?