In figuur 1 zie je wat ik zag.

Figuur 1

Natuurlijk was dat maar een illusie. Het enige verschil tussen de  en de  is het streepje rechtsboven (kijk in figuur 2 hoe de cijfers er op de klok uitzien). En dat geldt ook voor de  en de . De klok liep gewoon vooruit en ik had het verkeerd gezien.

Dat roept natuurlijk de vraag op of alle streepjes even belangrijk zijn. Laten we in figuur 2 eens kijken naar alle mogelijke cijfers op een digitale klok.

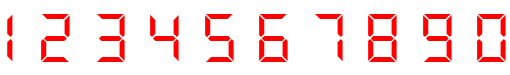
Figuur 2

Van de horizontale streepjes zijn het bovenste en het middelste belangrijk. Het bovenste bepaalt het verschil tussen de  en de , de middelste tussen de  en de . Maar het onderste horizontale streepje heeft eigenlijk geen functie! Dek het streepje maar eens af met een strook papier en kijk goed. Je kunt nog altijd zonder enige twijfel zien welk cijfer bedoeld wordt.

De verticale streepjes aan de linkerkant zijn ook allebei nodig. Het bovenste bepaalt het verschil tussen de  en een , het onderste het verschil tussen de  en de , maar ook tussen de  en de .

Van de streepjes aan de rechterkant hadden we aan het begin al gezien dat het bovenste nodig is. Maar het streepje rechtsonder is volledig overbodig. Als het streepje rechtsonder niet functioneert, weet je toch nog precies welke cijfer de klok aangeeft.

Je zou een digitale klok zelfs met twee streepjes minder kunnen maken zonder dat er twijfel is over de bedoelde cijfers. Kijk maar in figuur 3 wat er was gebeurd als het blaadje rechtsonder had gezeten.

Figuur 3

Elk cijfer is uniek te bepalen, want de overblijvende streepjes vormen voor elk cijfer nog steeds een uniek patroon. Alle zichtbare streepjes zijn wel echt nodig, omdat er anders verwarring kan ontstaan.

Redundant

Bij een digitale klok is dus niet elk streepje echt nodig. We zeggen dan dat de cijfers op een digitale klok een redundant systeem zijn. Dat betekent zoveel als: je kunt informatie weglaten zonder dat de functie verloren gaat.

Bij de klok is het toeval, maar soms wordt er aan systemen opzettelijk redundantie toegevoegd. Een goed voorbeeld is de data op een CD-rom. De informatie op een CD wordt opgeslagen in blokjes van telkens vier bits: dus viermaal een 0 of een 1. Daarmee kun je in totaal zestien ($ = 2 \times 2 \times 2 \times 2$) symbolen coderen. Maar bij een CD-rom doen ze iets slims: aan elke vier bits voegen ze drie extra bits toe. Op de manier zoals in de tabel.

Getal		Informatie					Extra				Getal		Informatie					Extra
0		0	0	0	0		0	1	1		8		1	0	0	0		1	0	1
1		0	0	0	1		1	0	0		9		1	0	0	1		0	1	0
2		0	0	1	0		0	0	0		10		1	0	1	0		1	1	0
3		0	0	1	1		1	1	1		11		1	0	1	1		0	0	1
4		0	1	0	0		1	1	0		12		1	1	0	0		0	0	0
5		0	1	0	1		0	0	1		13		1	1	0	1		1	1	1
6		0	1	1	0		1	0	1		14		1	1	1	0		0	1	1
7		0	1	1	1		0	1	0		15		1	1	1	1		1	0	0

 

De drie extra bits worden niet voor niets toegevoegd. Het is redundante (dus: overbodige) informatie, waardoor de CD bijna altijd leesbaar blijft, ook als er krassen op zitten! (Krassen op een CD zijn vergelijkbaar met het blaadje voor de streepjes van een digitale klok.)

Kijk maar eens goed naar elk rijtje van zeven enen en nullen. Je kunt pas op een ander bestaand rijtje van zeven bits terechtkomen, als je minstens drie enen en nullen uit het rijtje verandert (van een 0 een 1 maken of andersom).

Dus als van een rijtje van zeven bits er eentje stuk gaat (bijvoorbeeld door een kras), weet de CD-speler nog altijd welk getal er eigenlijk werd bedoeld. Het apparaat zoekt gewoon het rijtje op dat maximaal op één positie anders is dan de ingelezen bits. Probeer het zelf maar uit.

Opgave

Zoek maar eens uit welke getallen bij de volgende rijtjes van bits horen (telkens is er één bit onjuist).

1001001     0011010     0000000     0001010

Deze codering wordt ook wel Hamming-code genoemd naar de uitvinder Richard Hamming. Het is een voorbeeld van een zogenaamde ‘foutcorrigerende code’. Dat is informatie, opgeslagen in bits, die zich kan herstellen van (niet te grote) leesfouten. Dankzij de redundantie. In bijna alle data-transmissie wordt van dit soort systemen gebruik gemaakt.

We zouden de zeven streepjes op onze digitale klok dus nog veel effectiever kunnen gebruiken. Bijvoorbeeld door de cijfers 0 tot en met 9 af te beelden met de Hamming-code (de informatie zetten we op de vier verticale streepjes, de extra bits op de horizontale), zoals in figuur 4.

Figuur 4

Dan hebben we een digitale klok die zeer ongevoelig is voor fouten door overhangende planten! (Alleen jammer dat het dan voor mensen niet meer leesbaar is.)

Bekijk oplossing