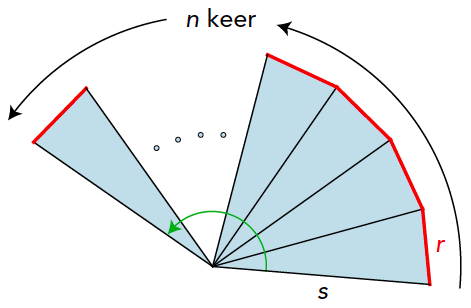
Een gewone waaier is in feite niets anders dan een aaneenrijging van congruente gelijkbenige driehoeken. In figuur 1 zie je een waaier van $n$ driehoeken met zijden $r$ (basis) en $s$ (de twee gelijke zijden). Kun jij formules bedenken voor de lengte van de rand (rood), de oppervlakte (blauw) en de hoek (groen)? Alle drie de formules bevatten een factor $n$, want de rand, oppervlakte, en hoek zijn evenredig met het aantal $n$. Als $n$ groeit, groeien de rand en de oppervlakte op een evenredige manier. De drie formules geven we aan het eind van het artikel.

Doorwaaieren

Kunnen we een waaier maken van eindig veel papier, die écht kan doorwaaieren? Kijk maar eens naar figuur 2. De rechthoekige driehoeken zijn gelijkbenig en gelijkvormig, maar niet meer congruent zoals de waaier in figuur 1. De waaier in figuur 2 zou je een ‘fractale waaier’ kunnen noemen, want als je de grootste driehoek weghaalt, is dat wat overblijft in feite precies dezelfde waaier, alleen een maatje kleiner. Wat zijn de lengte van de totale rand (rood), de totale oppervlakte (blauw) en de totale hoek (groen)? 

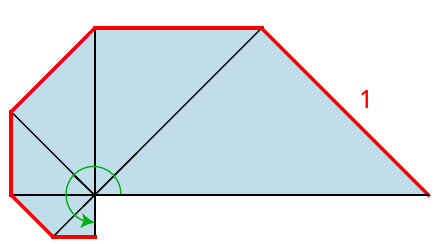
De lengte van de rand is gelijk aan

$$1+ \frac{1}{2}\sqrt{2} + \frac{1}{2} + \frac{1}{4}\sqrt{2} + \frac{1}{4} + \frac{1}{8} \sqrt{2} + \frac{1}{8} +…=2+ \sqrt{2}.$$

Je kunt dit zelf narekenen, gebruikmakend van de formule voor de som van een meetkundige rij. Als we de onderkant van de grootste driehoek ook nog meerekenen, heeft de waaier een omtrek van 2 + 2√2. De som van alle oppervlaktes – die helaas nog wel over elkaar heen liggen – is 1 en de totale hoek is oneindig.

Zonder overlap

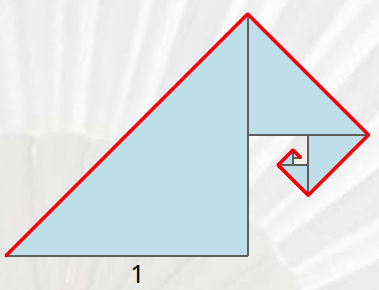
Kunnen we de stukken zodanig aan elkaar leggen, dat de waaier niet meer over zichzelf heen waaiert? Uit figuur 3 blijkt dat dat inderdaad kan. De vorm van de driehoeken hoeven we er niet eens voor aan te passen, wel laten we de tweede, vierde, zesde, ... driehoek uit figuur 2 ongebruikt.

De som van alle rode zijden in figuur 3 is gelijk aan 2√2 en de som van de zwarte zijden aan de buitenkant van de figuur is gelijk aan 2. We komen (toevallig?) weer op een totale omtrek van 2 + √2. De totale oppervlakte is gelijk aan $\frac{2}{3}$.

Gulden snede

Kunnen we de driehoeken schalen, opdat deze figuur nét niet overlapt? Hier biedt de gulden snede uitkomst. In figuur 4 is een rechthoek zó in tweeën gesplitst, dat geldt:

$$\frac{x}{1} = \frac{1}{x −1}.$$

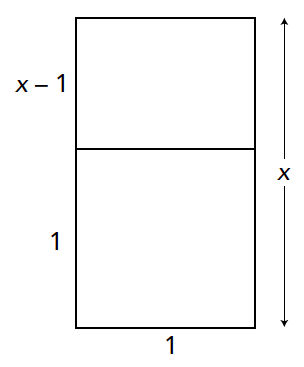
Deze vergelijking heeft als unieke positieve oplossing $x = \frac{1}{2} (1 + √5)$. De grote (gehele) rechthoek en de kleine rechthoek zijn gelijkvormig. De kleine rechthoek kun je volgens dezelfde verhouding in tweeën splisten. Als je dit proces eindeloos voortzet, en in de vierkanten die zo ontstaan gelijkbenige, rechthoekige driehoeken plaatst, krijg je de waaier in figuur 5.

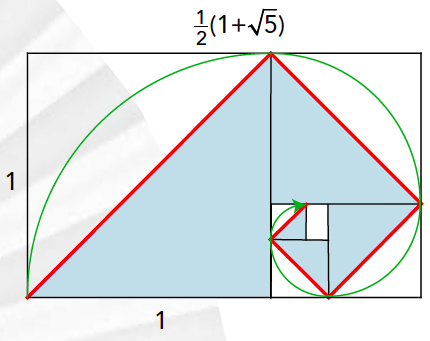
De totale oppervlakte van de waaier kan je prachtig aflezen. Deze is $\frac{1}{4} (1 + √5)$. Zie je waarom? 

De totale lengte van de rand is lastiger; probeer die zelf eens uit te rekenen.

De pan uit rijzen

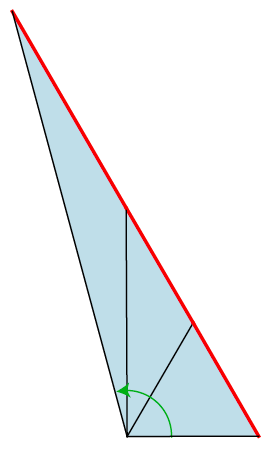
We blijven nog even bij gelijkbenige driehoeken, maar de rechte hoeken laten we vallen. In figuur 6 zie je een manier om zo’n waaier te maken. Alle driehoeken zijn gelijkbenig en de eerste is zelfs gelijkzijdig. Deze waaier rijst echt de pan uit. Het enige eenvoudige aan deze constructie is de totale hoek: zie je waarom die $120^\circ$ moet zijn? Wat gebeurt er met de totale hoek als we een andere driehoek kiezen als eerste driehoek?

Spiraal van Theodorus

Van de waaiers in de figuren 2, 3 en 5 konden we de totale lengte en de totale oppervlakte berekenen, omdat de opeenvolgende termen steeds kleiner werden: ze kwamen willekeurig dicht bij nul. Je zou kunnen denken dat zulke reeksen wel altijd een eindige som hebben. Maar een tegenvoorbeeld laat zien dat zulke reeksen soms toch exploderen. De harmonische reeks

$$1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \ldots$$

rijst de pan uit, omdat er steeds een groep groter is dan $\frac{1}{2}$.

In figuur 7 zie je een waaier waarin alle driehoeken rechthoekig zijn, en alle korte (rode) zijden hebben lengte 1. Hierdoor zijn de ‘spaken’ vanuit punt O oude bekenden geworden: die hebben achtereenvolgens lengte 1, √2, √3, √4, √5, … Het is duidelijk wat er gaat gebeuren met de totale rand en de totale oppervlakte: die exploderen. De individuele hoeken worden kleiner en kleiner en komen willekeurig dicht bij nul. Zou de totale hoek begrensd zijn?

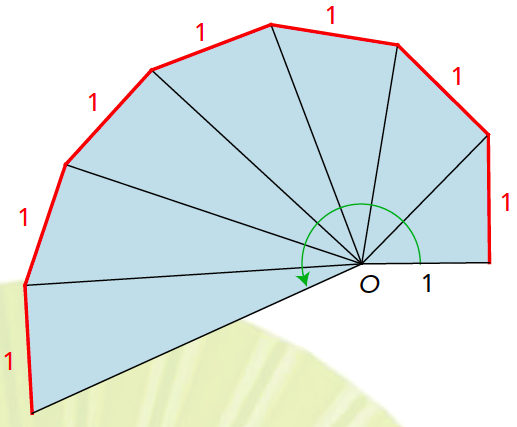
Het antwoord is nee, want de som van de hoeken is gelijk aan

$$\sin^{-1}\left(\frac{1}{\sqrt{2}}\right) +\sin^{-1}\left(\frac{1}{\sqrt{3}}\right) + \sin^{-1}\left(\frac{1}{\sqrt{4}}\right) + ...$$

en aangezien

$$\sin^{-1}\left(\frac{1}{\sqrt{n}}\right)>\frac{1}{\sqrt{n}}>\frac{1}{n}$$

explodeert de totale hoek sneller dan de harmonische reeks.

Deze waaier is al bestudeerd sinds de Oudheid en heet de spiraal van Theodorus. Theodorus, leraar van Plato, gebruikte de spiraal waarschijnlijk om wortels van getallen mee te construeren. Theodorus liet de constructie stoppen bij de zestiende driehoek.

Als je er willekeurig lang mee door zou gaan, zouden er dan op den duur twee schuine zijden kunnen samenvallen? Het is niet evident dat dat niet zo is. Pas in 1958 bewees Erich Teuffel dat twee schuine zijden nooit samenvallen.

Hoe snel groeit eigenlijk de hoek van de waaier in figuur 7? Probeer dat zelf eens uit te zoeken.

Veredelde harmonische waaier

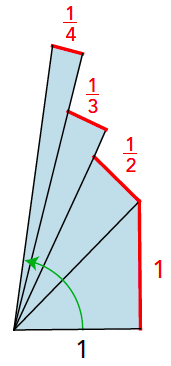
Als laatste bekijken we de zogenaamde veredelde harmonische waaier. Je ziet hem in figuur 8. De spaken hebben – net als in figuur 7 – achtereenvolgens lengte 1, √2, √3, √4, √5, … De overstaande rechthoekszijden hebben lengte 1, $\frac{1}{2} , \frac{1}{3} , \frac{1}{4} , \frac{1}{5}, …$

De rand komt dus neer op de harmonische reeks en wordt willekeurig groot. Ook de totale oppervlakte gaat naar oneindig. Maar hoe groeit de hoek? Ach, laat maar waaien! (Voor wie het toch weten wil: de totale hoek heeft een eindige som, want de hoeken zijn kleiner dan hun tangenswaarden en de som van de tangenswaarden is eindig volgens de integraaltoets voor reeksen. Maar die kennis vereist wiskunde die de middelbare school overstijgt...) 

 

Bekijk oplossing