De ruimtelijke figuren die we in de vorige artikelen binnenstebuiten keerden, bestonden uit een gesloten aaneenschakeling van gelijke meetkundige objecten: een gesloten band. De figuren in dit artikel zijn ingewikkelder en zullen we omkeren door middel van een band met een begin en een einde: een open band. Omdat de omgekeerde band weer dezelfde band is als de oorspronkelijke, noemen we deze band (waar we straks piramides op plakken) de invariant.

We beschrijven bijvoorbeeld hoe een rombendodecaëder (ruitvormig twaalfvlak) kan worden omgekeerd, zodat een gewone dodecaëder, een kubus of een octaëder ontstaat.

Invariant

Stel je een ruimtelijke figuur voor en bekijk deze als een schil. We nemen aan dat van deze figuur een aaneengesloten uitslag is te maken. Een uitslag kan naar binnen of naar buiten worden gevouwd om een ruimtelijke figuur te krijgen. De ene figuur is dan de binnenstebuiten gekeerde vorm van de andere. Een dergelijke schil noemen we invariant als hij binnenstebuiten gekeerd dezelfde figuur oplevert.

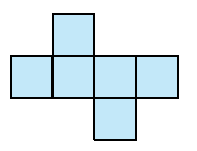
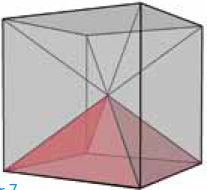
Neem bijvoorbeeld een kubus. We kunnen die kubus op vele manieren snijden en uitklappen tot een uitslag. Voorbeelden zie je in de figuren 1, 2 en 3. Om de kubus te maken, kunnen we de uitslag op twee manieren vouwen. We krijgen dan twee keer dezelfde figuur. De kubusschil kan daarom worden beschouwd als een invariant.

 

 

Extra eis 

We stellen nog een extra eis aan de invariant. Het is niet echt noodzakelijk voor de constructie, maar het zorgt ervoor dat het geheel er mooier uitziet. De invarianten worden zó gesneden, dat de uitslagen een lint vormen en dat, als de uiteinden van het lint aan elkaar worden bevestigd, alle vlakken zoveel mogelijk op dezelfde manier aan elkaar vastzitten. De uiteinden mogen natuurlijk alleen aan elkaar worden bevestigd als zo nog steeds de ruimtelijke figuur kan worden gemaakt.

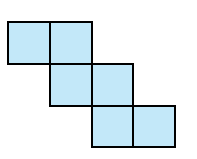
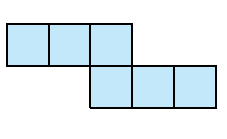
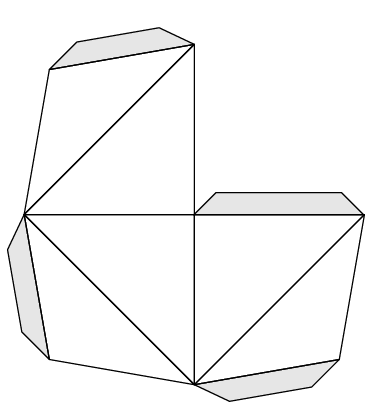
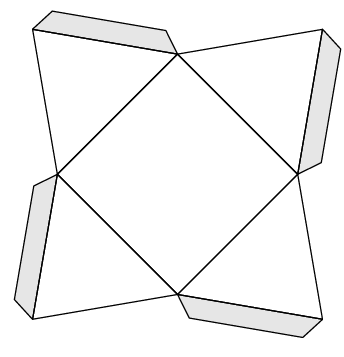
Neem de uitslagen van de kubus in de figuren 1, 2 en 3. In figuur 3 wordt het lint gevormd van het meest linkse naar het meest rechtse vierkant. Dit is een lint met twee flappen aan de zijkanten. Dus na het sluiten van het lint zijn er twee vierkanten die op een andere manier aan aan de andere vierkanten vastzitten (ze grenzen maar aan één ander vlak). In figuur 2 zien we een lint dat helemaal van links naar rechts loopt. Door het meest linkse vierkant aan de bovenzijde te bevestigen aan het meest rechtse vierkant aan de onderzijde, hebben deze twee vierkanten dezelfde begrenzing als de twee middelste vierkanten. De twee nog niet besproken vierkanten (de middelste van drie vierkanten op een rij) hebben echt andere buren. Ze grenzen op een andere manier aan twee vierkanten.

Door bij de uitslag van figuur 1 het meest linkse vierkant aan de bovenzijde te bevestigen aan het meest rechtse vierkant aan de onderzijde, krijgen alle vierkanten dezelfde begrenzing. Elk vierkant grenst op dezelfde manier aan twee andere vierkanten.

De constructiemethode 

De constructiemethode is opgebouwd rond de invariant van een ruimtelijk figuur. Hierbij wordt gebruik gemaakt van de ‘piramidemethode’ (zie het januarinummer) of een variant hierop. We nemen een figuur en beschouwen die in eerste instantie als massief en opgedeeld in piramides met als grondvlak telkens één vlak uit de invariant. De piramides bevinden zich dus allemaal aan één zijde van de invariant. De invariant is omkeerbaar en hiermee is de combinatie ook omkeerbaar, omdat we weten dat de piramides de ruimtelijke figuur vormen en dus in de invariant passen.

Doordat de figuur invariant is en omdat de vlakken van de invariant de grondvlakken zijn van de piramides, zullen de piramides na het omkeren in precies de andere richting wijzen. Zaten de piramides eerst in de invariant, na het omkeren zitten ze aan de buitenzijde. Hiermee wordt de invariant leeg.

De constructiemethode kan dan zelfs worden uitgebreid met het opnieuw toepassen van de piramidemethode op dezelfde massieve figuur. Dit hoeft natuurlijk niet. Deze nieuwe piramides kunnen dan aan de andere zijde van de invariant worden bevestigd.

Als variatie op de constructiemethode kunnen de piramides minder hoog worden genomen. Dit past dan zeker binnen de invariant. Het is zelfs met bepaalde ruimtelijke figuren mogelijk om in plaats van piramides andere vormen te gebruiken.

Het triakis-tetraëder

Een triakis-tetraëder is een tetraëder waarbij aan elke zijde een driehoekige piramide is geplakt. Om dit object binnenstebuiten te kunnen keren, kunnen we gebruikmaken van de tetraëder als invariant. Hiertoe gebruiken we de uitslag in figuur 4. Als we het lint sluiten tot een band, dan zien we dat alle vlakken dezelfde begrenzing hebben. We passen vervolgens de piramidemethode slechts één keer toe op de (massieve) tetraëder. Op deze manier zien we voor het omkeren van de invariant de invariant zelf (tetraëder) en na het omkeren een figuur die erg lijkt op een triakistetraëder. Deze laatste figuur wordt door de piramides met de invariant samen gevormd. (Als we de piramides iets kleiner zouden nemen, krijgen we wel een echte triakis-tetraëder.)

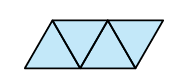
Om de constructie te maken, hebben we de ribbenlengtes van de piramides nodig. De lengtes van de ribben in het grondvlak weten we al, omdat we die zelf hebben gekozen. Maar de lengtes van de ribben die samenkomen in de top van de piramide moeten we nog berekenen. Laten we deze ribben de ‘topribben’ noemen. Alle toppen van de piramides komen samen in het zwaartepunt van de tetraëder en het zwaartepunt ligt op alle hoogtelijnen van de tetraëder. Het zwaartepunt is dus het snijpunt van de hoogtelijnen. In het kader op pagina 11 berekenen we de ribbenlengtes.

Van kubussenoctaëder naar rombendodecaëder

Ook voor deze constructie gebruiken we de piramidemethode; een keer op de gebruikelijke manier en een keer gebruiken we kleinere piramides. De grootte van deze laatste piramides is speciaal gekozen. 

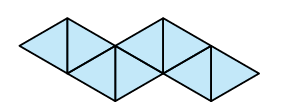
Laten we eerst naar de uitslag van de invariant (octaëder) kijken (zie figuur 5). Als de meest linkse driehoek wordt bevestigd aan de meest rechtse driehoek door de onderzijde van de linkerdriehoek te bevestigen aan de bovenzijde van de rechterdriehoek, krijgen alle driehoeken dezelfde begrenzing en zo kan de octaëder nog steeds worden gevormd. 

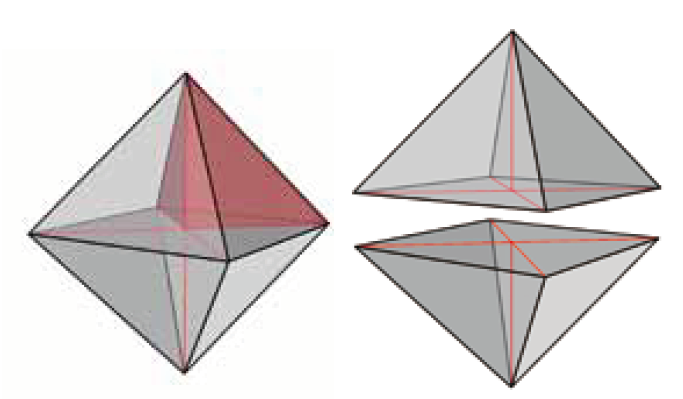
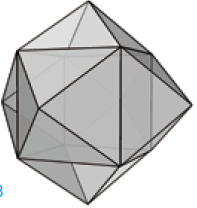
Nu kijken we naar de piramides die ontstaan met de piramidemethode. Een ervan is in rood weergegeven in figuur 6. Voor deze gewone piramides hebben we ook hier de lengte van de topribben nodig. In dit geval is deze makkelijk uit te rekenen.De octaëder is opgebouwd uit twee tegen elkaar geplaatste piramides met ieder een vierkant grondvlak (zie figuur 6). Het zwaartepunt van de octaëder valt precies in het zwaartepunt van het vierkant.

Veronderstel dat de ribbenlengtes van de octaëder (en dus ook de zijden van het vierkant) 2 zijn, dan kun je met behulp van de stelling van Pythagoras de diagonaal van het vierkant bepalen: $2\sqrt{2}$. Deze lengte is twee keer de ribbenlengte van de piramides. Dus $\sqrt{2}$ is de lengte van de topribben. 

We kunnen de piramides vervolgens op de invariant bevestigen en omkeren. Met deze piramides aan de buitenzijde ontstaat een figuur die lijkt te zijn opgebouwd uit hoeken van kubussen. We noemen dit een kubussenoctaëder. Je ziet hem op de laatste foto die bij de bouwtekening voor deze constructie staat.

Aan de andere zijde van de invariant bevestigen we vervolgens minder hoge piramides. Dit zijn de piramides die bij de tetraëder zijn bepaald. De zijden van het grondvlak van deze piramides moeten lengte 2 hebben. Dit is de ribbenlengte van de octaëder, maar ook van de tetraëder. Zoals we hebben gezien bij de berekening bij de tetraëder, moet de lengte van de topribben $\frac{1}{2}\sqrt{6}$ zijn.

Als we deze piramides aan de nog niet gebruikte zijde van de invariant bevestigen en naar buiten keren, ontstaat een mooie ruimtelijke figuur. De vlakken van de piramides vormen ruiten; in totaal worden er twaalf ruiten gecreëerd. De zo ontstane figuur is een rombendodecaëder. Een leuke bijkomstigheid van deze constructie is dat er twee aan elkaar vastzittende kubussen kunnen worden gevormd (zie foto bij de bouwtekening).

Van kubus naar rombendodecaëder

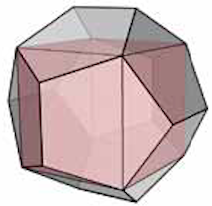
Bij deze constructie met de kubus als invariant maken we eveneens gebruik van de piramidemethode (zie figuur 7). Dit doen we maar één keer. Voor de uitslag van de invariant nemen we de uitslag van figuur 1. Als we de invariant omdraaien, met hieraan de piramides bevestigd, dan ontstaat ook hier de rombendodecaëder (zie figuur 8), net zoals bij de octaëder! Dit is eveneens te zien op de vierde foto in figuur 15. Na het omkeren van de invariant is deze natuurlijk leeg. Je kunt dit zo laten, zoals we hebben gedaan, of je kunt opnieuw de piramidemethode gebruiken, maar er zijn ook andere mogelijkheden, waarover straks meer.

We hebben opnieuw de lengtes van de topribben nodig. Dit is de helft van de lengte van de hoofddiagonaal van de kubus. Stel dat de ribbenlengte van de kubus 2 is. De hoofddiagonaal heeft dan lengte $2\sqrt{3}$ en de lengtes van de ribben van de piramides zijn dus $\sqrt{3}$.

Van kubus naar dodecaëder 

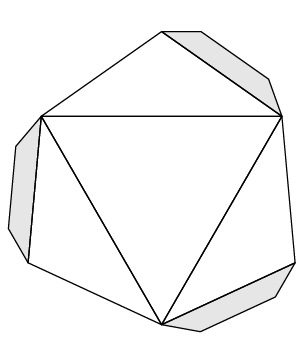
Het is mogelijk om een dodecaëder te krijgen door een soort ‘schilddakjes’ op een kubus te plaatsen. In het januarinummer hebben we uitgelegd hoe de kubus als hulpmiddel kan worden gebruikt om de lengte van de hoofddiagonalen in een dodecaëder te bepalen. Dit deden we door een kubus in de dodecaëder te plaatsen (zie figuur 9). Nu kunnen alle stukjes die buiten de kubus vallen (de zogenaamde ‘schilddakjes’) worden gebruikt voor de constructie. Door de schilddakjes op de buitenzijde van de invariant te plaatsen, krijgen we dus de dodecaëder. En het is mogelijk om de invariant om te draaien met de schilddakjes inbegrepen. De vormen passen in de kubus! We werken dit hier niet verder uit.

Je kunt je misschien wel voorstellen dat er zo een combinatie is te maken waarbij de rombendodecaëder, na het omdraaien, overgaat in de dodecaeder, met als invariant de kubus. Of de combinatie van kubus naar dodecaëder.

Bouwtekeningen

De bouwtekeningen voor de tetraëder en de kubus als invariant bestaan uit een (grond)vlak van deze invarianten en de driehoekszijden van de piramides (zie figuur 10 en 14). De bouwtekening voor de octaëder als invariant is opgebouwd uit de driehoekszijden van twee piramides (zie figuur 12). Hier komt dus geen vlak van de octaëder in terug. Het vlak valt geheel in de constructie van de piramides.

 

Nadat je de bouwtekeningen hebt gekopieerd (ze staan ook op www.pyth.eu) en in elkaar hebt geplakt, kun je de onderdelen aan elkaar bevestigen zoals in de foto’s is te zien. Voor het kunnen omkeren van de ruimtelijke figuren, moet er voldoende ruimte tussen de onderdelen zitten, zo’n 1 à 1,5 millimeter. De onderdelen kun je bijvoorbeeld met plakband aan elkaar bevestigen. Om de randen van het plakband vervolgens weg te werken, kun je een laagje papier op de oppervlakken plakken. In verschillende kleuren is dat het leukst!

 

 

De ribbenlengte van de piramides in de tetraëder 

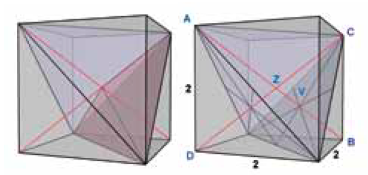
Als hulpmiddel voor het bepalen van de ribbenlengte van de piramides in de tetraëder gebruiken we de kubus. De tetraëder kan zó in een kubus worden geplaatst, dat de hoeken van de tetraëder samenvallen met vier hoeken van de kubus (zie figuur 16). In figuur 16 is verder in rood aangegeven hoe de piramides ontstaan. In figuur 17 zie je de doorsnede die is genomen over het vlak $ADBC$.

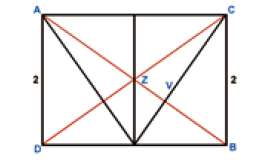
Trek een lijn van $A$ naar $B$; dit is een van de hoofddiagonalen van de kubus. Deze lijn loopt precies door het zwaartepunt van het vlak $V$ van de tetraëder. Dit kun je als volgt inzien. Alle drie de hoekpunten van de gelijkzijdige driehoek $V$ zijn ook hoekpunten van de kubus en zitten even ver van $A$. De afstand is namelijk de lengte van de diagonaal van de zijvlakken van de kubus. De hoekpunten zitten ook even ver van $B$. Deze afstand is gelijk aan de lengte van de ribben van de kubus. In feite zitten de drie hoekpunten even ver van elk willekeurig punt op de lijn $AB$, dus ook van het snijpunt van lijn $AB$ met vlak $V$. Bij een gelijkzijdige driehoek betekent dit dat dit snijpunt samenvalt met het zwaartepunt van de driehoek.

Dit betekent ook dat de lijn $AB$ loodrecht op $V$ staat. Daardoor valt deze lijn samen met de hoogtelijn van de tetraëder. De hoogtelijn loopt precies door het zwaartepunt van de tetraëder. Deze lijn hebben we dus nodig voor de constructie. 

Neem nu nog een andere hoofddiagonaal van de kubus ($CD$). De twee hoofddiagonalen snijden de kubus precies in het zwaartepunt van de kubus. Omdat beide diagonalen samenvallen met twee hoogtelijnen van de tetraëder, is dit zwaartepunt ook het zwaartepunt $Z$ van de tetraëder! Het is nu gemakkelijk om de lengte van $AZ$ en $CZ$ te bepalen. Deze lijnstukken zijn de topribben.

Neem aan dat de ribbenlengte van de kubus 2 is. De ribbenlengte van de tetraëder is dan $2\sqrt{2}$. En de lengte van de hoofddiagonaal van de kubus is $2\sqrt{3}$.

De twee diagonalen $AB$ en $CD$ snijden elkaar dus precies in het zwaartepunt van de kubus/tetraëder. Daarmee wordt de lengte van de ribben precies de helft van deze lengte: $\sqrt{3}$.

Omdat we uitgaan van de tetraëder met een vooraf bepaalde lengte van de ribben (bijvoorbeeld 2), kunnen we alle lengten van de ribben van de kubus, de tetraëder en van de piramides in de voorgaande berekening met dezelfde factor aanpassen zodat de ribbenlengte van de tetraëder 2 wordt. Deze factor is $\frac{1}{2}\sqrt{2}$. De lengte van de topribben wordt dan $\frac{1}{2}\sqrt{2} \times \sqrt{3} = \frac{1}{2}\sqrt{6}$.