Welke route, met een zo klein mogelijke totale lengte, brengt ons langs alle twaalf Nederlandse provincies? De route mag een verschillend begin- en eindpunt hebben. Wel moeten we even goed afspreken welk vervoermiddel ik op het oog heb. Niet de trein, niet de auto, maar… de helikopter. Ik wil dus een reis langs de twaalf provincies maken die hemelsbreed – of, zoals de Engelsen zo fraai zeggen, ‘as the crow flies’ – gemeten een minimale lengte heeft. Elke plek in een provincie telt uiteraard mee.

Het gaat er bij deze vraag niet om de exacte minimale afstand te bepalen, maar om de verrassende uitkomst. Hoe loopt die route?

Oplossing

Na enig teken- en nadenkwerk kom je wellicht tot de conclusie dat het gunstig is om via ‘2-provinciënpunten’ en ‘3-provinciënpunten’ te reizen. Dat schiet namelijk lekker op. Zo kun je de route bijvoorbeeld starten in het 3-provinciënpunt van Groningen, Friesland en Drenthe. Vervolgens vlieg je naar het 3-provinciënpunt van Overijssel, Flevoland en Gelderland (waarbij je ‘toevallig’ het 3-provinciënpunt van Friesland, Drenthe en Overijssel aandoet, maar nodig is dat niet). Dan vlieg je door naar het 3-provinciënpunt van Zuid-Holland, Zeeland en Noord-Brabant, maar pas op: deze lijn maakt een lichte knik omdat we Noord-Holland anders overslaan. Ten slotte gaan we naar het 2-provinciënpunt van Noord-Brabant en Limburg. Deze route zie je in figuur 1.

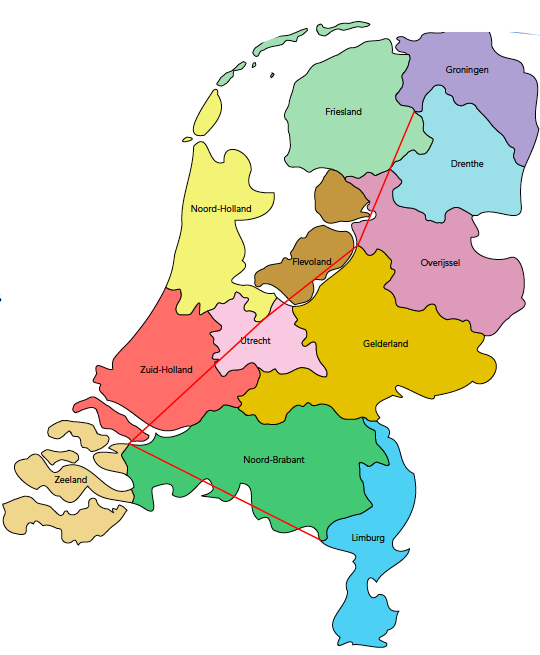
Er is echter een kortere route! Je ziet hem in figuur 2. De rechte lijn tussen het 3-provinciënpunt van de drie noordelijke provincies en dat van Zuid-Holland, Zeeland en Noord-Brabant gaat namelijk ‘toevallig’ door Overijssel, Flevoland, Noord-Holland en Utrecht. Zorgvuldig meten levert een bekorting van ongeveer 1,5% ten opzichte van de route in figuur 1.

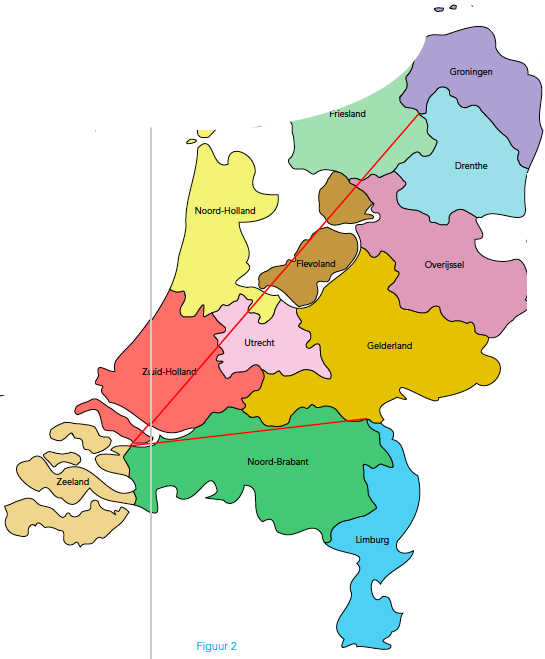
Meer problemen voor reislustigen

Stel, in een vierkant land wonen mensen die erg van reizen houden. Het land wordt opgedeeld in zes provincies op zo’ n manier dat je binnen een provincie elk punt kan bereiken zonder de provincie te verlaten. Hoe kan je de provincies zó over het vierkante land verdelen dat je maximaal moet reizen om bij alle provincies langs te komen? Het reizen gaat weer in vogelvlucht, dus in rechte lijnen, en we willen – ondanks dat er reislustige mensen in dit fictieve land wonen – niet meer reizen dan strikt noodzakelijk.

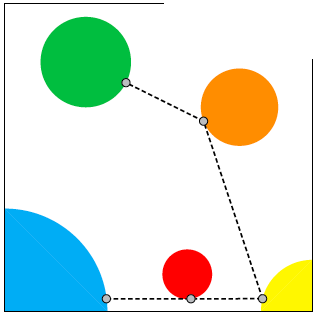
In het vierkante land dat je in figuur 3 ziet, zijn zes provincies getekend: vijf cirkelvormige provincies (gekleurd) en het witte gedeelte dat de zesde provincie vormt. Als we de lengte van een zijde van het vierkant op 1 zetten, dan is de afgebeelde afstand ongeveer 1,4. Is het de kortste afstand?

Als je de afgelegde reis zo lang mogelijk wilt maken, krijg je al gauw behoefte om de provincies te verkleinen. Laten we dit extreem doen, en doen alsof een enkel punt al een provincie is. Ons vierkante land wordt dan dus opgedeeld in vijf miniprovincies (elk een punt in het vierkant) en één grote provincie (het hele vierkant minus de vijf punten). Zodoende abstraheren we onze puzzel: hoe kan je vijf punten in het vierkant plaatsen, zodat de reis tussen de punten het grootst is? Wij komen tot 2 + √2, maar het zou best nog beter kunnen. Wij weten geen bewijs dat 2 + √2 optimaal is. 

Het is instructief om te beginnen met twee punten (dus drie provincies), en dit allengs op te bouwen (steeds in een vierkant van 1 $\times$ 1). Vind jij betere resultaten dan die in de volgende tabel?