Onlangs was ik toeschouwer bij een voetbalwedstrijd tussen Horta en Verto. Hoewel het een belangrijke wedstrijd was ging het er zo tam aan toe dat ik mijn toevlucht zocht tot iets anders. De rechthoekige tribune zat helemaal volgepakt. De Horta-fans in hun lichtblauwe outfit en de Verto-fans in het fletsoranje waren goed uit elkaar te houden. Ze zaten vriendschappelijk door elkaar. Aanvankelijk viel me eigenlijk weinig op. Ik probeerde wat te tellen, wat niet zo goed lukte. En toen opeens zag ik een patroon. In elke rij bleken $14$ Horta-fans te zitten. Ik telde het nog een keer na, want dit kon toch haast niet waar zijn. Terwijl ik me zat af te vragen wat hiervan de oorzaak kon zijn, werd de wedstrijd spannender. Omdat het me niet losliet, keek ik later nog eens goed rond. Vanuit een ander perspectief bleek er nog iets ongeloofwaardigs aan de hand te zijn. In elke kolom zaten precies $11$ Verto-fans. Ik was met stomheid geslagen. Hoe hadden ze dat voor elkaar gekregen? Nou was ik zelf niet gekomen als fan van een van de teams (de scheidsrechter was een kennis van me). Ik keek nogmaals goed rond of ik de enige neutrale kijker was. Met wat moeite telde ik $16$ anderen die niet als fan herkenbaar waren. De wedstrijd ging nu geheel langs me heen. Eenmaal thuisgekomen wist ik niet eens wat de uitslag was. De volgende dag boog ik me nog eens over die getallen. En toen viel pas het meest bijzondere op. Er zijn wel meer afmetingen van tribunes waarbij me dit had kunnen overkomen. Echter, de tribune van gisteren bleek de kleinste te zijn waarbij zich dit kon voordoen. Hoeveel zitplaatsen waren er?

Dit is een herformulering van het laatste probleem, opgave 30, van de Kangoeroewedstrijd 2022 voor HBO en WO studenten, genaamd wizEXPERT. Dit niveau is dit jaar als experiment toegevoegd aan de gangbare reeks wizFUN, wizKID, wizSMART, wizBRAIN en wizPROF, die gericht zijn op groep 3 van de basisschool tot en met klas 6 van het VWO. De hele reeks opgaven van wizEXPERT is te vinden op w4kangoeroe.nl.

Hoe los je zoiets op? Probeer het eerst zelf maar eens. Eigenlijk moet je geen antwoord willen krijgen. Dat ontneemt je de lol van het zelf puzzelen. En dan leer je er ook niet zo veel van.

Als je toch een hint wilt, dan kan ik je verklappen dat de deelnemers aan wizEXPERT konden kiezen uit de volgende vijf mogelijke antwoorden:

$A$ 500

$B$ 660

$C$ 690

$D$ 840

$E$ 994

Aanpak

Er zijn wat algemene strategieën om problemen op te lossen.

Begin maar eens met namen te geven aan onbekenden, zodat je kan opschrijven wat je hiervan weet in de vorm van formules. Daarna kun je mogelijk wat rekenen of algebra bedrijven. Wat zijn hier goede onbekenden om te benoemen?

Mocht dat niet genoeg opleveren dan kun je het probleem "kleiner" maken. Er zitten drie, ogenschijnlijk arbitraire, numerieke constanten in dit probleem: $14$ Horta-fans per rij, $11$ Verto-fans per kolom en $17$ neutro's (de neutrale kijkers). Die aantallen zijn net wat te groot om diagrammen te maken. Je zou eens kunnen kijken wat je met kleinere aantallen kan. Ikzelf dacht aan nul neutro's, en daarna één. Of drie Horta's per rij en twee Verto's per kolom (er blijken dan tien neutro's te zijn). Met die kleine aantallen kun je eens wat diagrammen van mogelijke stoelverdelingen proberen op te maken.

De vragen bij de Kangoeroewedstrijd en de A-vragen van de eerste ronde van de Nederlandse Wiskunde Olympiade zijn multiple choice vragen. Je kan die antwoorden proberen. Kun je een rechthoek met $500$ zitplaatsen vullen volgens de gegeven aantallen? Zo ja, dan is antwoord A goed. Zo nee, dan onderzoek je vervolgens met antwoord B.

Een oplossing, in twee stappen

Het is goed om in de gaten te houden dat het draait om het totale aantal zitplaatsen op de tribune, niet om de afmetingen. Maar we weten iets over rijen en kolommen. Daarom ligt het voor de hand om het aantal rijen en aantal kolommen een naam te geven, zeg r rijen en k kolommen. Wat weten we daar zoal van?

1. $rk$ is het totale aantal zitplaatsen; dat willen we minimaliseren
2. $r \ge 11$, want elke kolom bevat in elk geval $11$ Verto-fans
3. $k \ge 14$, want elke rij bevat in elk geval $14$ Horta-fans
4. $14r + 11k + 17 = rk$ want de tribune zit vol

Als je wat combinaties van $r$ en $k$ probeert, dan zie je al snel dat die meestal niet werken. Daarvoor moet je wel rekenen en het levert weinig op. Zo kom je er niet uit. Je zou een oplossing kunnen zoeken voor $14r + 11k + 17 = 500$, om te controleren of antwoord A goed is. Met wat handigheid lukt dat wel: $r = 18$ en $k = 21$ (dit is zelfs de enige geheeltallige oplossing met $r \ge 11$ en $k \ge 14$). Wat betekent dat? Als antwoord A goed is, dan moet gelden $r = 18$ en $k = 21$. Maar dat betekent nog niet dat antwoord A goed is. Als we de eerste eis controleren, dan valt deze combinatie door de mand: $rk = 378 \neq 500$. Je kan ook meteen wat rekenen aan de vierde eis. Deze is als volgt te herschrijven:

$14r + 11k + 17 = rk \Leftrightarrow$
$rk - 14r - 11k = 17 \Leftrightarrow$
$(r - 11)(k - 14) - 11 \times 14 = 17 \Leftrightarrow$
$(r - 11)(k - 14) = 171$

Die laatste vorm is handig, omdat we geheeltallige oplossingen zoeken. Blijkbaar kan $171$ geschreven worden als een product. Hoe? Daartoe ontbinden we $171$ in factoren: $171 = 32 \cdot 191$. De tabel hieronder geeft de $(2+1)(1+1) = 6$ mogelijkheden om $171$ als product van twee factoren te schrijven en de bijbehorende oplossingen voor $r$ en $k$.

$1^e$ factor	$3^0\cdot 19^0$	$3^1\cdot 19^0$	$3^2\cdot 19^0$	$3^0\cdot 19^1$	$3^1\cdot 19^1$	$3^2\cdot 19^1$
$r-11$	$1$	$3$	$9$	$19$	$57$	$171$
$k-14$	$171$	$57$	$19$	$9$	$3$	$1$
$r-11$	$12$	$14$	$20$	$30$	$68$	$182$
$k-14$	$185$	$71$	$33$	$23$	$17$	$15$
$rk$	$2220$	$994$	$660$	$690$	$1156$	$2530$

Ook hier zien we dat $500$ afvalt, en ook $840$ (antwoord C). Het kleinste aantal zitplaatsen is $660$ (antwoord B), verkregen met $r = 20$ en $k = 33$. Maar is dat het goede antwoord? Die vergelijking is een noodzakelijke voorwaarde, maar is het ook een voldoende voorwaarde? Lukt het om met deze afmetingen de tribune te vullen met $14$ Horta-fans in elk van de $20$ rijen en $11$ Verto-fans in elk van de $33$ kolommen? Dit bleek lastiger dan ik had verwacht. Het werd 'prutswerk'. Uiteindelijk stuitte ik op een oplossing. Maar ik werd er niet blij van, want die zag er vreselijk uit. Bovendien wilde ik weten of de vijf andere mogelijkheden uit de tabel ook te realiseren waren. En toen, ineens, 'zag' ik het. Vul de eerste rij, van links uit, met $14$ Hortafans. De eerste $14$ kolommen hebben nu één plek minder voor een Verto-fan dan de resterende kolommen. In de tweede rij gaan we verder met weer $14$ Horta-fans, vanaf de kolom waar we gebleven waren (kolommen $15$ t/m $28$). Nu is ook in die kolommen een plek minder voor Verto-fans. Als je dit cyclisch blijft herhalen (d.w.z. als je rechts aan het einde van de rij komt, dan ga je weer bij de meeste linkse stoel verder), dan krijg je gegarandeerd $14$ Horta-fans in elke rij. Bovendien zijn deze verticaal zo goed mogelijk gespreid. Hoeveel lege plaatsen zijn er nu in elke kolom (om Verto fans en neutro's te plaatsen)?

Stel dat in de laatste rij de laatste Horta-fan in kolom $K$ terechtkomt. Dan bevatten de kolommen $1$ t/m $K$ hetzelfde aantal lege plekken, en de kolommen vanaf kolom $K + 1$ één meer. In figuur 1 is een voorbeeld met $3$ Horta-fans in elk van $6$ rijen op een tribune die $7$ kolommen breed is.

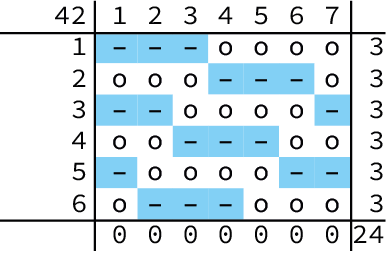
Je ziet dat kolommen $1$ t/m $4$ drie Horta-fans hebben en de kolommen $6$ t/m $7$ twee. Dit is makkelijker te bevatten als je alle Horta-fans in hun kolom naar boven laat aansluiten. Er zijn dan twee volle rijen met Horta-fans en één gedeeltelijk gevulde rij. Kolom $4$ (waar de laatste Horta- fan zit) is te berekenen als $(6 \times 3)\ mod\ 7$, waarbij $a\ mod\ b$ de rest geeft na deling van $a$ door $b$. Het aantal van twee Horta-fans in de kolommen $5$ t/m $7$ is te berekenen als $\lfloor (6 \times 3)/7\rfloor$ , waarbij $\lfloor a/b\rfloor$ het quotiënt bij deling van $a$ door $b$ zonder rest is. De kolommen $1$ t/m $4$ hebben één Horta-fan meer. We kunnen dus nul, een, twee of drie Verto-fans per kolom garanderen (en de rest is dan voor neutro's).

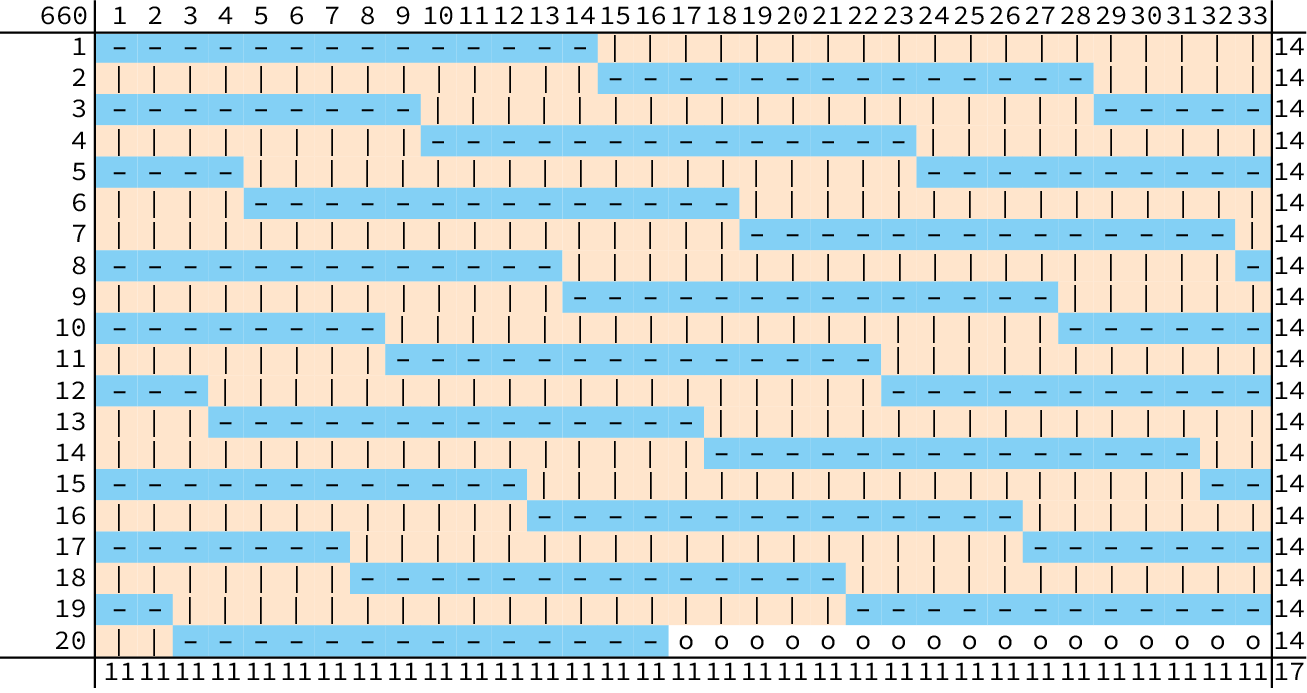
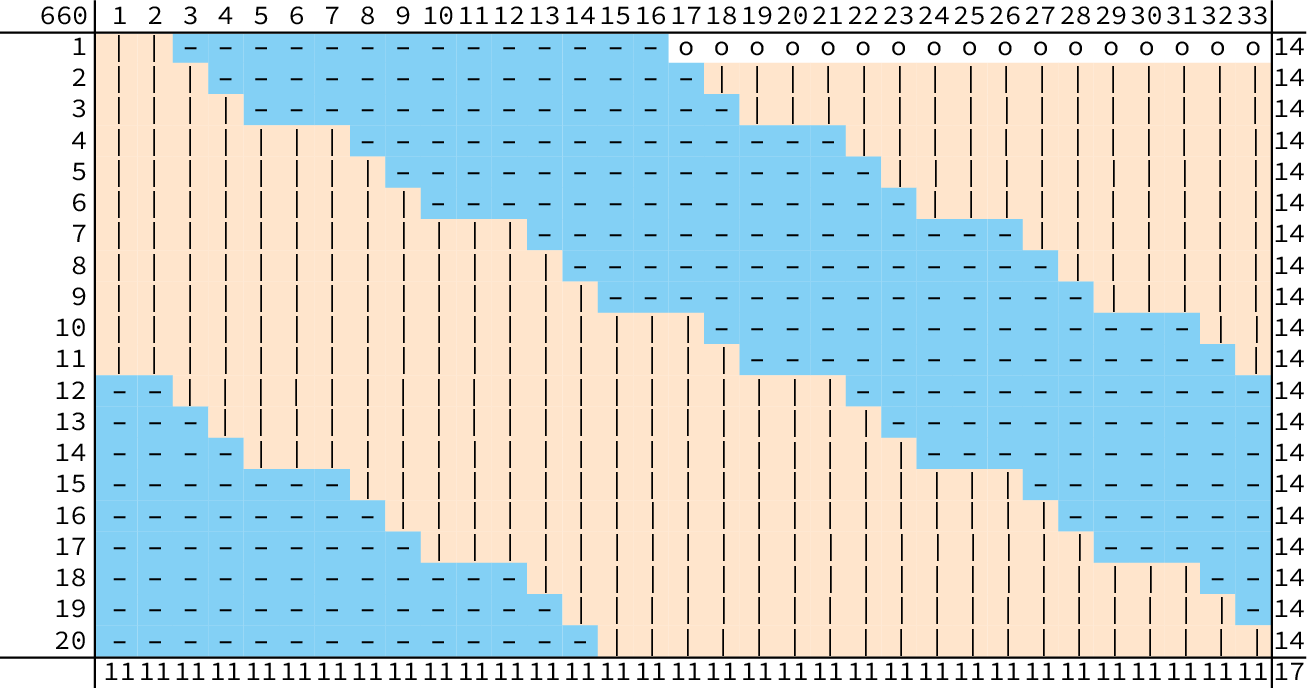
Als we zo voor $r = 20$ en $k = 33$ in elke rij $14$ Horta-fans plaatsen, dan zit de laatst geplaatste Horta-fan in kolom $(20 \times 14)\ mod\ 33 = 16$. Vanaf kolom $17$ zijn er dan $\lfloor(20 \times 14)/33\rfloor = 8$ Horta-fans per kolom, en in kolommen $1$ t/m $16$ één meer, dus $9$. Daar kunnen dus $11$ Verto-fans zitten per kolom. In de kolommen $17$ t/m $33$ zitten dan ook nog $17$ neutro's. Zie ook figuur 2a. Door rijen te verwisselen blijft het een oplossing. In figuur 2b hebben we de rijen gesorteerd, waardoor diagonale groepen van fans ontstaan. Deze constructie werkt in het algemeen.

Slotbeschouwing

Het oplossen van zulke problemen vereist natuurlijk enige wiskundige voorkennis. Maar daarnaast is ook voldoende wiskundige creativiteit nodig om die kennis zo toe te passen dat het probleem bezwijkt. Bij het oplossen van dit probleem kom je drie belangrijke gebieden van de wiskunde tegen: algebra (bij het herschrijven van de vergelijking), getaltheorie (bij het ontbinden van gehele getallen en modulair rekenen) en combinatoriek (bij het systematisch vinden van arrangementen).