Kijk eens naar deze vergelijking:

$$12 = 3 + 4 + 5.$$

Een fraai exemplaar, al zeggen we het zelf. Want precies de cijfers 1, 2, 3, 4 en 5 zijn gebruikt, en nog in deze volgorde ook. Aan de linkerkant van het =-teken staat een getal dat uit de cijfers 1 en 2 bestaat, en aan de rechterkant staan losse cijfers en twee maal de bewerking +. 

Kijk vervolgens naar

$$12 = (1 + 1) \times 2 \times 3.$$

De linkerkant bevat opnieuw de cijfers 1 en 2, terwijl de rechterkant een expressie is met de bewerkingen $+, \times$, nog eens $\times$, en de cijfers 1, 1, 2 en 3. Samen zijn nu de cijfers 1, 1, 1, 2, 2, 3 gebruikt, ofwel drie maal een 1, twee maal een 2 en één maal een 3.

Nu kijken we naar

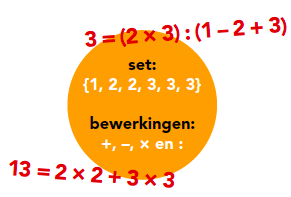
$$13 = 2 \times 2 + 3 \times 3.$$

Hier staat opnieuw links een getal, en rechts een expressie. Als je de cijfers telt, kom je uit op één maal een 1, twee maal een 2 en drie maal een 3. 

Zelf aan de slag

Kan je met een gegeven set van cijfers een kloppende gelijkheid maken? We hebben verschillende soorten problemen opgesteld. Bij veel opgaven is het al moeilijk om één voorbeeld te bedenken. Maar er zijn ook sets waarmee je juist meer dan één gelijkheid kunt maken. Met de cijfers 1, 2, 2, 3, 3, 3 kun je $13 = 2 \times 2 + 3 \times 3$ maken (zoals we hierboven zagen), maar bijvoorbeeld ook $3 = (2 \times 3) : (1 – 2 + 3)$.

Wat is het grootste getal dat je met 1, 2, 2, 3, 3, 3 kunt maken? We spreken in dat geval van de extreme variant: hoe krijg je het grootste getal aan de linkerkant bij een gegeven set van cijfers?

De onderdelen A tot en met F staan in volgorde van moeilijkheidsgraad gesorteerd. Je mag zelf kiezen welke onderdelen je maakt. Niets hoeft je ervan te weerhouden om direct met een moeilijk onderdeel aan de slag te gaan!

Bij elke opgave krijg je een set cijfers en de bewerkingen die je mag gebruiken. Haakjes mag je gebruiken zo veel je wilt. Je kunt elke opgave op twee manieren maken:

• normaal: de opdracht is om een getal aan de linkerkant te verkrijgen.
• extreem: je gaat op zoek naar het grootst mogelijke getal (in sommige gevallen is dit heel moeilijk!).

Onderdeel A

De sets cijfers zijn achtereenvolgens $\{1, 2, 3, 4\}, \{1, 2, 3, 4, 5\}, \{1, 2, 3, 4, 5, 6\}, \{1, 2, 3, 4, 5, 6, 7\}, \{1, 2, 3, 4, 5, 6, 7, 8\}, \{1, 2, 3, 4, 5, 6, 7, 8, 9\}.$ Je gebruikt alleen de bewerkingen + en –.

Onderdeel B

De set cijfers bestaat uit een aantal keer $\{1, 2, 3, 4, 5, 6, 7, 8, 9\}$. Het aantal kopieën dat je mag gebruiken is 2 tot en met 10. Je gebruikt alleen de bewerkingen + en –.

Onderdeel C

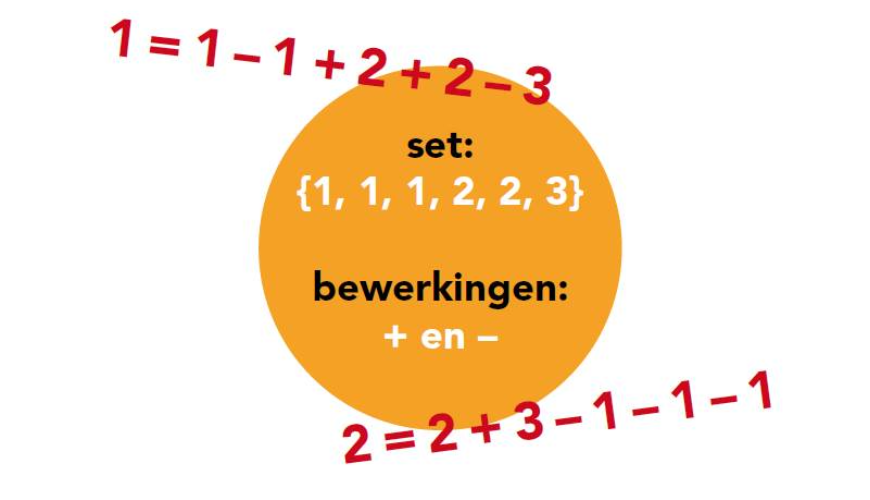
De sets cijfers zijn achtereenvolgens $\{1, 1, 1, 2, 2, 3\}, \{1, 1, 1, 1, 2, 2, 2, 3, 3, 4\}, \{1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5\},$ enzovoorts, tot en met 9.

Je gebruikt de bewerkingen +, –, $\times$ en :.

Onderdeel D

De sets cijfers zijn achtereenvolgens $\{1, 2, 3, 4\}, \{1, 2, 3, 4, 5\}, \{1, 2, 3, 4, 5, 6\}, \{1, 2, 3, 4, 5, 6, 7\}, \{1, 2, 3, 4, 5, 6, 7, 8\}, \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$.

Je gebruikt de bewerkingen +, –, $\times$ en :.

Onderdeel E

De set cijfers bestaat uit een aantal keer $\{1, 2, 3, 4, 5, 6, 7, 8, 9\}$. Het aantal kopieën dat je mag gebruiken is 2 tot en met 5. 

Je gebruikt de bewerkingen +, –, $\times$ en :.

Onderdeel F

We gebruiken achtereenvolgens $\{1, 2, 2\}, \{1, 2, 2, 3, 3, 3\}, \{1, 2, 2, 3, 3, 3, 4, 4, 4, 4\}, \{1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5\},$ enzovoorts. Je mag ook boven de 10 gaan. Je gebruikt dan tien keer de 10, elf keer de 11, enzovoorts. De getallen 10, 11, 12, … mogen alléén aan de rechterkant van de gelijkheid staan. Ook deze opgave kun je ‘normaal’ en ‘extreem’ oplossen. Bij de extreme variant is de oplossing een tabel waarin voor elk getal (groter dan 3) staat wat het grootst te maken getal is. Natuurlijk is dit nooit groter dan

$$999999999888888887777777666666555554444333221.$$

Kun je dit getal met een zekere set maken? Dit is een moeilijke vraag, maar we hopen dat jullie er ver mee komen. Veel succes!

Inzenden

Iedereen kan aan de prijsvraag meedoen: leerlingen, beroepswiskundigen, hobby.sten, enzovoorts. Ook als klas kun je inzenden. De jury verdeelt het prijzengeld – in totaal 200 euro – onder de inzenders met de interessantste resultaten. Inzenden kan alleen digitaal. Mail je inzending naar [email protected]. 

Vermeld duidelijk met welke onderdelen je bent bezig geweest. Ook in deelresultaten zijn we geïnteresseerd! 

Vermeld verder je naam en adres, en als je scholier bent, de naam en het adres van de school, je leeftijd en je klas. Bij een klasseninzending moet bovendien de naam van de wiskundedocent opgegeven worden. Inzendingen moeten uiterlijk 14 april 2018 bij ons binnen zijn.