De naam 'Oelami' is afgeleid van de achternaam van Stanislaw Ulam, een Poolse (en later Amerikaanse) wiskundige. Ulam is de bedenker van veel wiskundige problemen en vermoedens. Eén daarvan is bekend onder de naam Ulam's Game. De oorspronkelijke vraag gaat over het volgende spel: een speler neemt een getal tussen 1 en 1 000 000 in gedachten. De andere speler mag ja/nee vragen stellen.

Als de eerste speler niet liegen mag, kan de andere speler met elke vraag het aantal overgebleven getallen steeds halveren; die heeft dan maximaal $20$ vragen nodig. Maar wat gebeurt er als de eerste speler maximaal één keer mag liegen?

Dit spel lijkt een beetje flauw, maar eigenlijk zijn computers hier de hele tijd mee bezig. Een computer verstuurt informatie als $0$-en en $1$-en (bits). Het kan gebeuren dat een $0$ door ruis onderweg bij de ontvanger als een $1$ wordt gezien, of andersom. Dit gebeurt niet zo heel erg vaak, maar wel af en toe. Stel dat het gemiddeld één keer gebeurt per twintig bits. Dat lijkt al aardig op Ulam's game, want er zijn $2^{20}$ mogelijke rijtjes van twintig bits, en elk verstuurde bit is het ja/nee antwoord op een vraag, waarbij verminking van het antwoord overeenkomt met een leugen. 

Bij Oelami kies je niet uit $1\,000\,000$ getallen, maar uit $15$ objecten. Dat komt overeen met een rijtje van $4$ bits, waarbij de combinatie $'0000'$ niet wordt gebruikt. Als je niet mag liegen dan kun je het gekozen object altijd 'raden' met maximaal vier ja/nee vragen $(2^4 = 16)$. Hoe zit het als je maximaal één keer mag liegen? Het is duidelijk dat het niet meer lukt in vier vragen. Maar is vijf vragen dan genoeg? Of zes? En hoe moet je dat dan doen? 

Je zou natuurlijk elke vraag twee keer kunnen stellen. Omdat er maximaal één keer gelogen mag worden zou je altijd hetzelfde antwoord moeten krijgen. Als je merkt dat je bij een vraag twee verschillende antwoorden hebt gekregen dan stel je die vraag gewoon nog een derde keer. De meerderheid van antwoorden is voor die vraag dan de waarheid. Je hebt in dat geval dus maximaal $4 \times 2 + 1 = 9$ vragen nodig. Zou het ook met minder vragen kunnen? 

We formuleren het probleem nu wat wiskundiger: we gaan aan alle objecten een identificatie toekennen, een zogenaamd codewoord. Een codewoord bestaat uit $N$ bits. Hoe groot $N$ is laten we nog even in het midden. Niet alleen moeten alle codewoorden anders zijn, het moet ook zo zijn dat wanneer je één of twee bits in een codewoord verandert, je niet uitkomt op een ander codewoord. Probeer zelf te bedenken waarom het ook belangrijk is dat om één leugen te herkennen een woord na twee veranderingen nog steeds geen ander codewoord mag zijn. 

We hebben dus een lijst nodig van $16$ codewoorden van $N$ bits. Als de eerste speler (we noemen haar de zender) een object heeft gekozen verstuurt ze het bijhorende codewoord. Als de andere speler (de ontvanger) een woord ontvangt dat niet in de codelijst staat dan probeert hij telkens één van de $N$ bits uit het ontvangen woord te veranderen zodat hij een woord krijgt dat wel in de codelijst staat (je mag 'hij' en 'zij' uiteraard ook anders lezen). Als er maximaal één keer gelogen is dan komt hier precies één bijhorend codewoord uit dat aangeeft welk object is gekozen.

We hebben nog geen keuze gemaakt voor $N$ en de $16$ codewoorden. Maar we kunnen nu wel gaan rekenen. We maken dus een lijst van $16$ woorden van $N$ bits. En voor elk van de $16$ woorden zijn er $N$ woorden die precies een bit anders zijn. Het totaal aantal verschillende woorden dat we dus minimaal moeten hebben is $A = 16 \times (N + 1)$. In de tabel staan wat waardes opgesomd.

$\ \color{\white}{N}\ $	$\ \color{\white}{2^N}\ $	$\ \color{\white}{A}\ $
$4$	$16$	$16\times(4+1)=80$
$5$	$32$	$16\times(5+1)=96$
$6$	$64$	$16\times(6+1)=112$
$7$	$128$	$16\times(7+1)=128$
$8$	$256$	$16\times(8+1)=144$

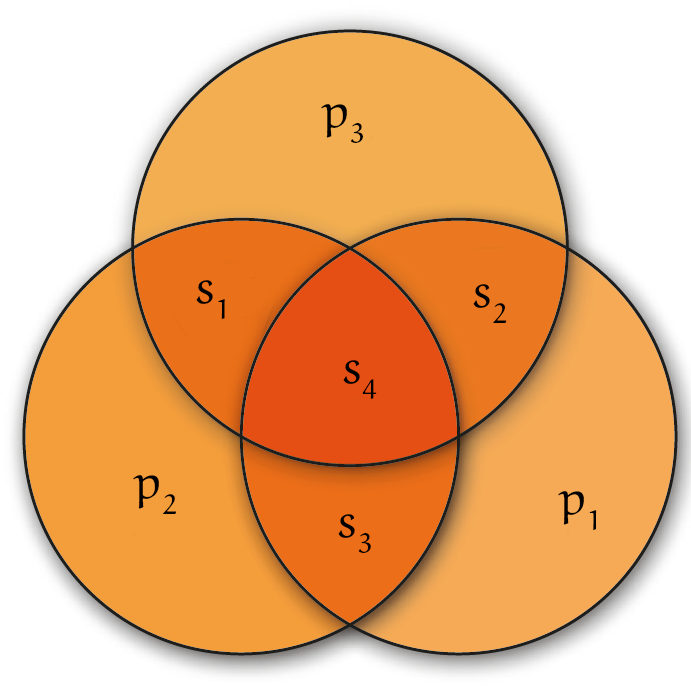
Het totaal aantal mogelijke woorden van $N$ bits is $2^N$. Een waarde voor $N$ gaat zeker niet werken als $A > 2^N$. Daarmee vallen $N = 4, 5, 6$ af. Pas bij $N = 7$ lijken we een kans te maken. Dat is wat beter dan $N = 9$ waar we eerder mee aankwamen. De Amerikaanse wiskundige Richard Hamming liet zien dat het met $N = 7$ precies kan. Beschouw daartoe het diagram hiernaast.

Voor elk van de $16$ $4$-bit woorden gaan we drie extra bits bepalen zodat we op $7$ bits uitkomen. We vullen de vier bits in het diagram in op de plekken $s_1$, $s_2$, $s_3$ en $s_4$. We berekenen de bits $p_1$, $p_2$ en $p_3$ door te zorgen dat binnen elke cirkel een even aantal $1$-en staat. Dat geeft de codes van $16$ $7$-bit woorden in de tabel hieronder. Voor de leesbaarheid hebben we tussen de $s$-bits en de $p$-bits van een codewoord een spatie geschreven: $s_1s_2s_3s_4\ p_1p_2p_3$. 

De code die nu is ontstaan heet een ${\rm Hamming}(7,4)$ code. Er zijn $128$ woorden van $7$ bits. Elk woord is ofwel een codewoord, of het verschilt op exact één positie van een codewoord. Dit wordt daarom een perfecte code genoemd. Door deze code te gebruiken kan een ontvanger een fout in maximaal één bit corrigeren. Dit heet daarom een $1$-foutcorrigerende code.

$\ \color{\white}{Object}\ $	$\ \color{\white}{Codewoord}\ $		$\ \color{\white}{Object}\ $	$\ \color{\white}{Codewoord}\ $
$0$	$0000\ 000$		$8$	$1000\ 011$
$1$	$0001\ 111$		$9$	$1001\ 100$
$2$	$0010\ 110$		$10$	$1010\ 101$
$3$	$0011\ 001$		$11$	$1011\ 010$
$4$	$0100\ 101$		$12$	$1100\ 110$
$5$	$0101\ 010$		$13$	$1101\ 001$
$6$	$0110\ 011$		$14$	$1110\ 000$
$7$	$0111\ 100$		$15$	$1111\ 111$

De foutcorrectie kun je nu simpel uitvoeren: de ontvanger plaatst de ontvangen bits in het diagram en kleurt elke cirkel waarin het aantal $1$-en oneven is rood. Het foute bit ligt binnen alle rode cirkels en buiten alle nog zwarte cirkels. Als er geen rode cirkels zijn dan was er geen fout opgetreden.

We gaan terug naar Oelami. Oelami is gebaseerd op de ${\rm Hamming}(7,4)$ code waarbij de $0$ niet wordt gebruikt. Elk getal correspondeert met een object op de indexkaart. Daarnaast zijn er zeven codekaarten, één voor elke bit in de codewoorden. Op de kaart met nummer $i$ staan alle objecten waarvan het bit op positie $i$ een $1$ is. In een hoekje staan in grijs de weegfactoren: $1$ t/m $8$ voor $s_1$ t/m $s_4$ en $0$ voor $p_1$ t/m $p_3$. De volgorde van de bits is wel iets  aangepast: $p_1p_2s_1p_3s_2s_3s_4$.

De zender neemt een van de $15$ objecten in gedachten en pakt alle kaarten waar dat object op staat. Dat komt dus overeen met het bijhorende codewoord. Om te liegen mag de zender of een kaart weglaten (dan verandert ze dus een $1$ in een $0$) of een kaart toevoegen (dan verandert ze een $0$ in een $1$). Het resterende stapeltje geeft ze aan de ontvanger. De ontvanger gebruikt het diagram om de leugen te achterhalen. Nu kun je ook zien dat op de kaarten die bij een $p$-bit horen een grijze $0$ staat. Op de kaarten die bij bit $s_i$ horen staat $2^{i-1}$. Zo kun je de grijze getallen bij elkaar optellen om te achterhalen welk object is gekozen.

Een verschil tussen Ulam's Game en Oelami is dat bij Ulam's Game de vragen na elkaar worden gesteld. Bij Oelami worden alle ja/nee antwoorden in één keer doorgegeven door de hele stapel te overhandigen. Wij hebben object $0$ weggelaten omdat dit object overeen zou komen met het overhandigen van een stapeltje met $0$ kaarten. Dat leek ons wat verwarrend. Veel plezier met Oelami.

Het spel is te vinden op kangoeroe.nl