Dit jaar zijn de covers niet-herhalende vlakvullingen. Op deze plaats tref je een uitleg aan bij de covers.

Omslag 63-5, april 2024: Heel veel pentomino’s

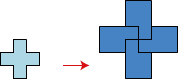
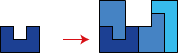
Hier wordt een voorbeeld van de substitutieregel getoond. We beginnen met een pentomino (een figuur dat bestaat aan 5 aaneengesloten vierkantjes. De regels staan hieronder. Elke keer vervang je elke pentomino door een set kleinere pentomino’s volgens deze regels. Er valt eenvoudig te bewijzen dat het resultaat een vlakvulling oplevert, die op geen enkele manier regelmatig is.

Hieronder zie je een detail van het omslag met daarin de vervangingen:

Omslag 63-4, februari 2024: Einstein voorzien van een fraai motief

De omslag laat exact dezelfde einsteins zien als de voorafgaande omslagen. Maar nu zijn de einsteins allemaal op dezelfde manier bedrukt. Hiernaast staat hoe de Einstein is bedrukt met een aantal gekleurde cirkelbogen. Er kan naar eigen believen enorm worden gevarieerd op dit thema. En stuk voor stuk zijn de resultaten prachtig!

Omslag 63-3, januari 2024: Einstein en de hoed, in groepjes

In het artikel dat hierboven wordt genoemd staat ook een beschrijving hoe je kunt komen tot een vlakvulling. Dat is een iteratief (herhalend) proces. De eerste stap is dat je steeds 7 of 8 Einstens samen brengt. Vervolgens neem je steeds 6 of 7 van die groepen samen en vorm je grotere groepen. En hier begint de iteratie. Steeds opnieuw neem je 6 of zeven van die groepen samen om te komen tot grotere groepen Einsteins.

Op de omslag is uitsluitend de eerste stap uitgevoerd. De verschillende groepen zijn steeds wit, grijs of zwart gekleurd, met uitzondering van een rode Einstein in het midden. Deze rode Einsteins zijn steeds het spiegelbeeld van de overige einsteins.

Omslag 63-2, november 2023: Einstein en de hoed

De tweede vlakvulling is van David Smith. Hij schreef hier vervolgens een artikel over samen met Craig S. Kaplan, Joseph Samuel Myers en Chaim Goodman-Strauss. David Smith is een hobbiist die al jaren op zoek was naar een enkel figuur waarmee hij een vlakvulling zou kunnen maken. En dan niet zo maar een willekeurige vlakvulling, maar een onregelmatige (zie de toelichting hierboven bij Omslag 63-1). Hij is trouwens niet de eerste die daarin is geslaagd. Al in 1988 bedacht Peter Schmitt een enkel figuur waarmee een onregelmatige vlakvulling gerealiseerd kon worden. Maar het figuur van Peter Schmitt bestond uit meerdere stukken. Daarna werd het doel om een figuur te vinden dat samenhangend zou zijn (dat wil zeggen dat het bestaat uit een aaneengesloten oppervlak). Precies dat realiseerde David Smith. De term Einstein moet je letterlijk nemen: "ein Stein", in het Duits. Dat was de verkorte beschrijving van de uitdaging. Het heeft helemaal niets te maken met Albert Einstein. De vorm doet erg veel denken aan een hoed.

Omslag 63-1, september 2023

De eerste vlakvulling is ontworpen door de wis- en natuurkundige Roger Penrose (zie nl.wikipedia.org/wiki/Roger_Penrose). Deze bestaat uit twee verschillende ruiten: enerzijds de witte en de donkerblauwe en anderzijds de rode en de lichtblauwe. Voordat hij zich bezig hield met onregelmatige vlakvullingen hadden onderzoekers al gekeken naar vlakvullingen die met een beperkt aantal (puzzel)stukjes gevuld kunnen worden, maar waarbij het bewezen kan worden dat dat nooit op een regelmatige manier kan.