Misschien kijk je wel eens in verveling naar het behang op de muur en zie je allerlei patronen. Een bevredigend gezicht voor een lui of verveeld brein. Wellicht word je zelfs geactiveerd om je behang nog eens wat beter te bestuderen. 'Wat nou als ik ondersteboven naar het behang kijk? Wat zie ik dan?' Of je hebt het geluk dat er een spiegel aan de muur hangt zodat je ook het spiegelbeeld van al die wonderlijke patronen kan zien.

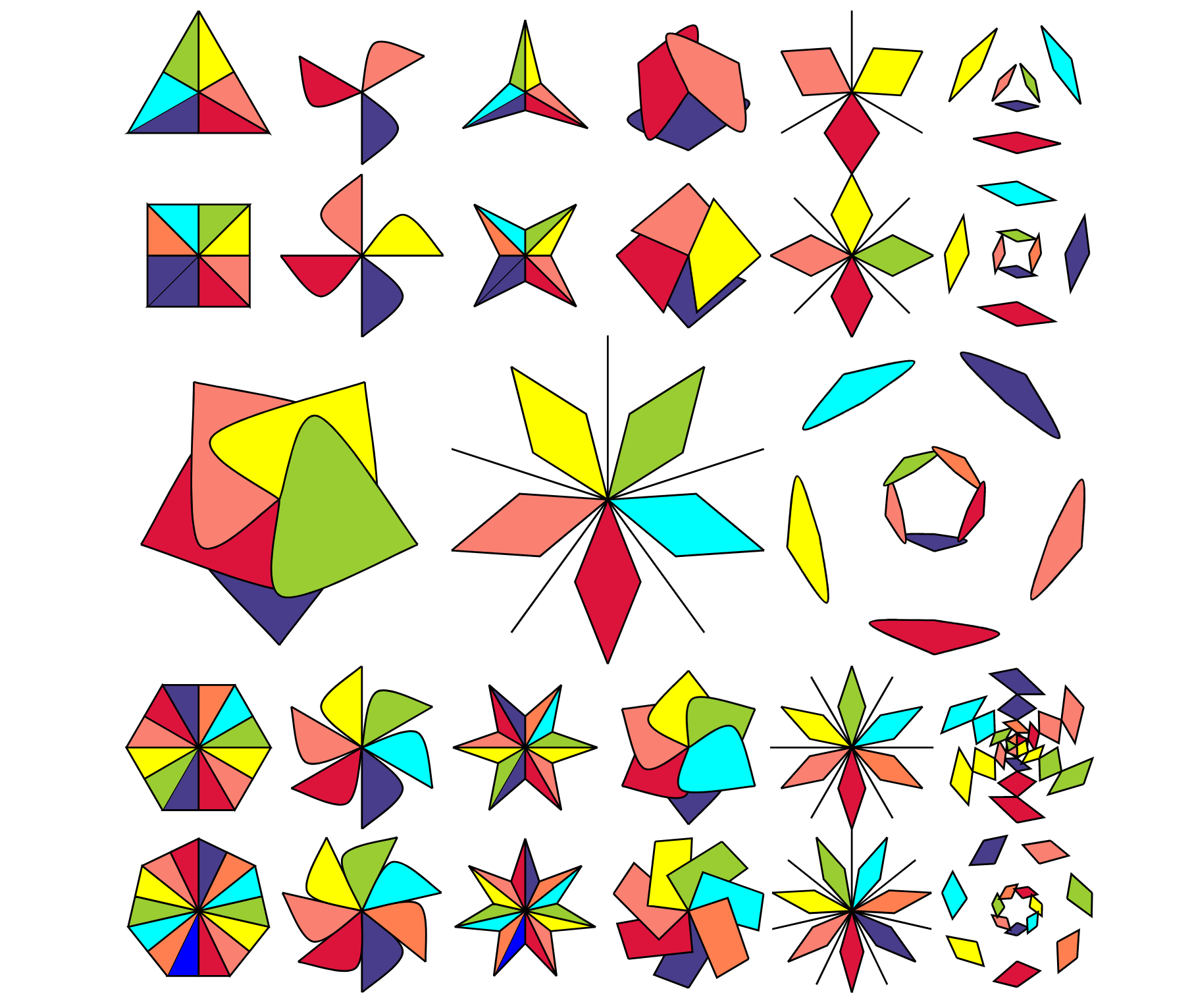
Wiskunde zit vol met symmetrieën, en zo ook dus wellicht jouw behang. In het boek Beautiful Symmetry van Alex Berke maken we kennis met de kunst en de wiskunde van patronen en symmetrieën. Al heb je nog nooit een snufje interesse in wiskunde gehad of ben je een fervent wiskunde nerd, dit boek kan voor iedereen wel tot de verbeelding spreken (letterlijk en figuurlijk). Voor de eerste groep zal het een interactieve wandeling zijn door een wereld van symmetrie, interactief omdat je wordt aangemoedigd om zelf in het boek te kladden voor een beter idee over symmetrie. Opbouwend is te lezen over symmetrie met spiegelbeelden of rotaties en lezer wordt gevraagd om op artistieke wijze symmetrieën weg te halen of juist toe te voegen, zoals bijvoorbeeld te zien is in figuur 1, waarin gevraagd werd om alle vormen zó in te kleuren dat ze geen draaisymmetrieën meer hebben. Voordat ze zijn ingekleurd, hadden ze nog wel draaisymmetrieën. Zo kunnen alle figuren in de eerste rij zonder kleur op drie manieren worden gedraaid zonder te veranderen.

Het spelen met de symmetrieën en vormen is zelfs een leuk alternatief voor sudoku’s of woordzoekers, je bent niet alleen artistiek bezig, ook word je tijdens het kleuren aan het denken gezet over de vele rotaties en spiegelingen. Voor de groep die wat meer met wiskunde heeft, zal het een mooie visualisatie van de structuur in wiskunde zijn. Het komt goed naar voren hoe de structuur die te zien is bij getallen, niet alleen aan die getallen is voorbehouden. Zoals wellicht in het begin al duidelijk werd, is het zelfs op het behang mogelijk om die wiskunde te ontdekken. Al lezend krijgen we een goed beeld van groepentheorie en aan het eind van het boek wordt zelfs een wiskundige toelichting gegeven van dat onderwerp. En zelfs als je groepentheorie al tot in de puntjes hebt bestudeerd en in al die abstractie bent verwikkeld aan de universiteit, dan zal dit boek als een bevestiging van alle pracht en praal van die wiskunde kunnen dienen. Nu begin ik toch nog maar eens over het behang. Stel dat we onze muur volplakken met het patroon uit figuur 2.

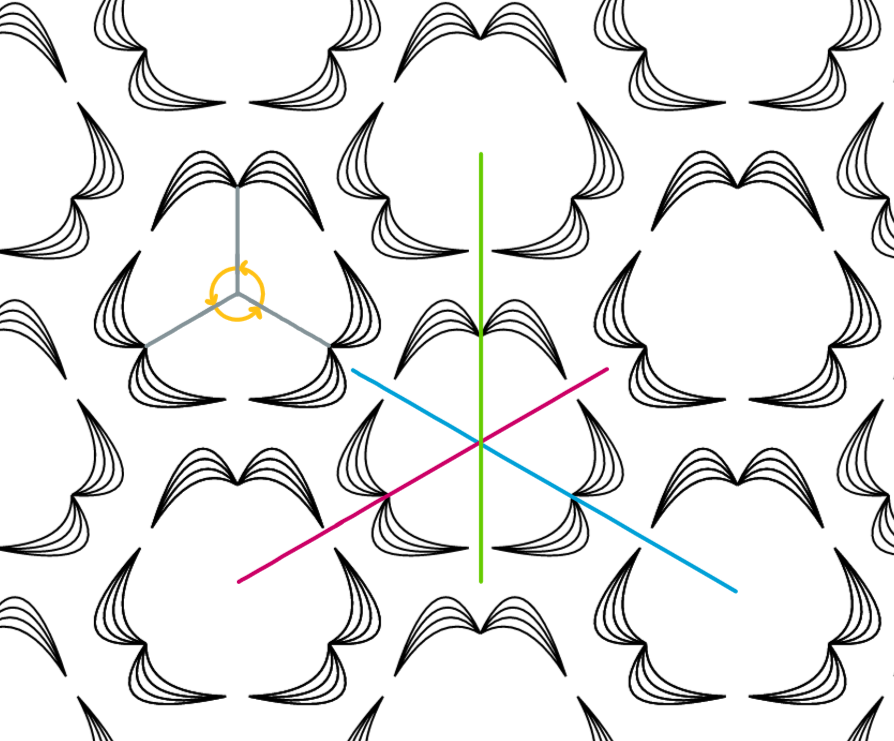
Wat is er interessant aan dit behang? Wellicht niet de eerste keuze voor iets wat we op de muur willen plakken. Dit behang zit echter wel boordevol symmetrie. Ten eerste is het op drie manieren te spiegelen. Stel dat je in een ondeugende bui bent en dit behang van de muur rukt, dan kan je het vervolgens steeds in drie richtingen vouwen zodat alles mooi op elkaar past, wel zo mooi bij het opvouwen. In figuur 3 is te zien wat hiermee wordt bedoeld. De groene, blauwe en roze lijn stellen symmetrieassen voor. Verder is met geel aangegeven hoe we de figuur kunnen roteren zonder hem te veranderen. Je zou het behang ook terug kunnen plakken, maar dan geroteerd. Als je het 120 graden draait, zowel linksom als rechtsom, dan kan je het terug plakken zonder dat iemand ziet dat er iets is veranderd! Nou ja, misschien komt het bij het plafond en de vloer wat minder mooi uit, maar wie kijkt daar nou naar? Bij dit behang kan je aan het denken worden gezet. In het boek word je uitgedaagd  om symmetrieën te veranderen, toe te voegen of te verwijderen. Hier zou je de drie spiegelsymmetrieën kunnen verwijderen en daarbij wel de draaisymmetrieën behouden. Terwijl je het behang probeert aan te passen kan je er ook nog iets moois van maken, bijvoorbeeld zoiets als in figuur 4, waarin we het nog wel steeds 120 graden kunnen draaien, maar niet meer kunnen spiegelen zonder het te veranderen. 

Zoals we hebben kunnen denken over de symmetrie in dit behang en bij die symmetrie ook een artistieke component kunnen betrekken, zo is er nog veel meer te vinden in het boek. Als spelen met patronen en symmetrieën je op deze manier aanspreekt, dan is Beautiful Symmetry zeker een aanrader!