Met de (blauwe) ruimtelijke zeshoek (afgekort Z-hoek) en de (grijze) rechthoek met een knik van $90^{\rm o}$ (afgekort L-hoek) uit figuur 1 kunnen Borromeaanse drietallen worden samengesteld. Zo'n drietal zit precies passend compact in elkaar, zoals we bijvoorbeeld in het vorige artikel zagen bij drie L-hoeken (figuur 2).

Het kan ook ruimer zoals met de drie L-hoeken in figuur 3. Indachtig het onderwerp verwacht je daar drie Borromeaanse drietallen. In figuur 3A is dat echter niet het geval. Daar zijn de drie L-hoeken gewoon tegen elkaar geschoven! door Klaas Lakeman OOO deel 2 In het Borromeaanse drietal van figuur 3B zitten de L-hoeken met een van hun hoekpunten in elkaar en in het drietal van 3C bij een van hun knikken. Ze lijken veel op elkaar. Sterker nog, feitelijk zijn ze hetzelfde, want door handig schuiven kunnen ze in elkaar over worden gevoerd. Dat is niet zo verbazingwekkend want bij het object in figuur 2 valt dat allemaal samen. Er kan daar niet worden geschoven. Als de L-hoeken in de figuren 3 niet vastgelijmd worden waar ze elkaar raken, blijven ze nauwelijks zitten. Bij figuur 3C is dat te ondervangen door kleine L-hoeken die elk met twee grote L-hoeken een Borromeaans drietal vormen (figuur 4).

Bij 3C (en ook 3B) komen door om het even welke van de drie L-hoeken door te knippen en weg te nemen de twee overgebleven L-hoeken volledig vrij te liggen (hét kenmerk van een Borromeaanse knoop). Om dat in figuur 4 te bereiken moeten om het even de grote en de kleine L-hoek van eenzelfde kleur worden doorgeknipt en weggenomen.

Opgave De kubusvorm in figuur 5 in bovenaanzicht bestaat uit drie grote ruimtelijke Z-hoeken die op een van z'n hoeken staat. Ga na of ze al dan niet Borromeaans met elkaar verstrengeld zijn.

ReChthoeken in iCosaëder

Op z’n Borromeaans - deel 1 eindigde met een opgave over Borromeaanse Gouden Rechthoeken. Een icosaëder of regelmatig twintigvlak heeft $12$ hoekpunten, $30$ randen of ribben en uiteraard $20$ zijvlakken. De randen of ribben liggen twee aan twee evenwijdig recht tegenover elkaar. Twee van die evenwijdige ribben spannen met twee ruimtediagonalen een rechthoek op. Zo zijn er $\frac{30}{2} = 15$ verschillende rechthoeken mogelijk binnen een icosaëder. Bij elk van die rechthoeken passen steeds twee andere congruente rechthoeken die daar loodrecht op staan (figuur 6A). Die drie vormen een Borromeaans drietal en hebben een gemeenschappelijk middelpunt dat samenvalt met dat van de icosaëder. Omgekeerd kun je ook zeggen dat die drie rechthoeken met hun $12$ hoekpunten de icosaëder opspannen. Dat het gouden rechthoeken zijn, is te berekenen maar ook snel in te zien door goed te kijken. 

Kijken

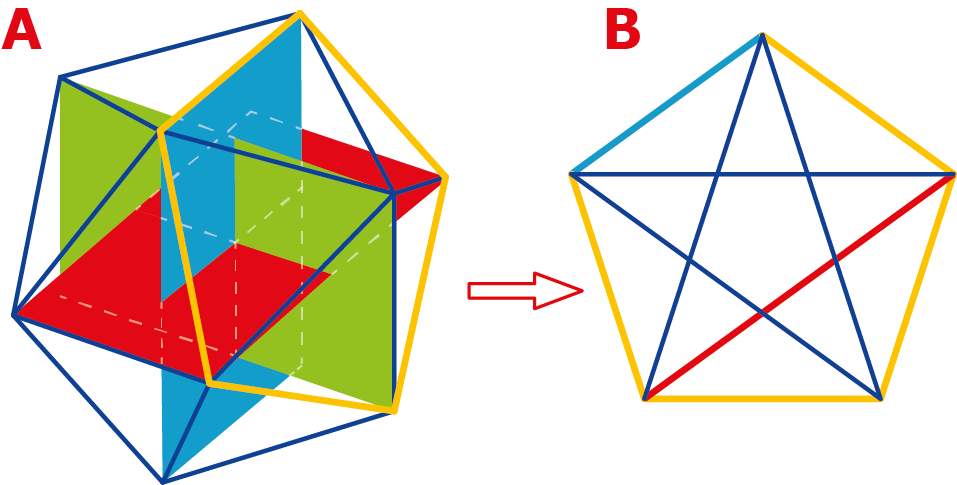
In de icosaëder van figuur 6A vormen de vijf $\color{goldenrod}{gele}$ randen een regelmatige vijfhoek. In figuur 6B is die er apart uitgelicht. Daarin is de rand die tevens een korte zijde van de $\color{blue}{blauwe}$ rechthoek is, $\color{blue}{blauw}$ gekleurd. Ook is daarin de diagonaal die tevens een lange zijde is van de $\color{red}{rode}$ rechthoek, $\color{red}{rood}$ gekleurd. Bekend is dat in een regelmatige vijfhoek een diagonaal en een zijde zich verhouden als de gulden snede. En daarmee verhouden de zijden van de rechthoeken in figuur 6A zich als het gulden getal. Het zijn dus gouden rechthoeken.

 

Bekijk oplossing